ЕГЭ. Профильный уровень. Задание 18
Свойства функций в задачах с параметрами
Часть 2
Дихтярь М.Б.
Монотонные функции
Замечания.
1. Если функции  и
и  определены и возрастают (убывают) на множестве Х, то функция
определены и возрастают (убывают) на множестве Х, то функция  +
+  возрастает (убывает) на этом множестве.
возрастает (убывает) на этом множестве.
2. Если функция  определена и возрастает (убывает) на множестве Х, то функция
определена и возрастает (убывает) на множестве Х, то функция  убывает (возрастает) на этом множестве.
убывает (возрастает) на этом множестве.
3. Если функции  и
и  определены и возрастают (убывают) на множестве Х и
определены и возрастают (убывают) на множестве Х и  для всех
для всех  то функция
то функция  возрастает (убывает) на множестве Х.
возрастает (убывает) на множестве Х.
Для того чтобы функция  , имеющая производную для каждого
, имеющая производную для каждого  , была возрастающей (убывающей) на множестве Х, необходимо и достаточно выполнения следующих условий:
, была возрастающей (убывающей) на множестве Х, необходимо и достаточно выполнения следующих условий:
1) 
2)  не равна тождественно нулю ни на каком промежутке, принадлежащем множеству Х.
не равна тождественно нулю ни на каком промежутке, принадлежащем множеству Х.
41. Найдите все значения параметра а, при которых функция  возрастает на всей числовой оси.
возрастает на всей числовой оси.
Решение. 1. Найдём производную

2. Найдём значения параметра а, при которых для всех  выполняется неравенство
выполняется неравенство

Ответ. 
42. Найдите все значения параметра а, при которых функция
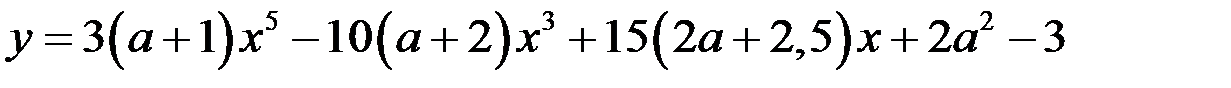 убывает для любого
убывает для любого  .
.
Решение. 1. Найдём производную

Найдём все значения параметра а, при которых для всех  выполняется неравенство
выполняется неравенство


2. Рассмотрим неравенство (1) при различных значениях параметра а.
1) Если  , то неравенство (1) принимает вид
, то неравенство (1) принимает вид  Так как последнее неравенство выполняется не для любого
Так как последнее неравенство выполняется не для любого  ,то
,то  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
2) Пусть  .
.
Если 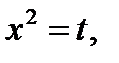 то неравенство (1) принимает вид
то неравенство (1) принимает вид

Замечание. Если для некоторого параметра  неравенство (2) имеет решение для любого
неравенство (2) имеет решение для любого  то и для параметра
то и для параметра  неравенство (1) имеет решение для любого
неравенство (1) имеет решение для любого  .
.
а) Пусть  Тогда неравенство (2) равносильно неравенству
Тогда неравенство (2) равносильно неравенству

Неравенство (3) имеет решение для любого  в трёх случаях.
в трёх случаях.
Неравенство (3) имеет решение для любого  если уравнение
если уравнение  имеет не более одного корня. Уравнение (4) имеет не более одного корня, если
имеет не более одного корня. Уравнение (4) имеет не более одного корня, если

Если  то неравенство (3) имеет решение для любого
то неравенство (3) имеет решение для любого  а тогда и для
а тогда и для  неравенство (1) имеет решение для любого
неравенство (1) имеет решение для любого  .
.
Неравенство (3) имеет решение для любого  если оба корня уравнения (4) отрицательные.
если оба корня уравнения (4) отрицательные.
Оба корня квадратного уравнения  с дискриминантом
с дискриминантом  , отрицательные, если
, отрицательные, если 
Уравнение (4) имеет два отрицательных корня, если

Итак, если  то неравенство (3) имеет решение для любого
то неравенство (3) имеет решение для любого  а тогда и для
а тогда и для  неравенство (1) имеет решение для любого
неравенство (1) имеет решение для любого  .
.
Неравенство (3) имеет решение для любого  если один корень уравнения (4) равен нулю, а другой корень отрицательный.
если один корень уравнения (4) равен нулю, а другой корень отрицательный.
Корень уравнения (4) равен нулю, если 
Рассмотрим уравнения (4), если  Имеем
Имеем

Итак, если  , то неравенство (3) имеет решение для любого
, то неравенство (3) имеет решение для любого  а тогда и для
а тогда и для  неравенство (1) имеет решение для любого
неравенство (1) имеет решение для любого  .
.
б) Пусть 
Рассмотрим неравенство

Пусть 
Так как графиком функции  является парабола, ветви которой направлены вверх, то найдутся значения
является парабола, ветви которой направлены вверх, то найдутся значения  для которых неравенство (5) не будет выполняться. Тогда
для которых неравенство (5) не будет выполняться. Тогда  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Ответ. 
Использование монотонности функций
для решения уравнений, неравенств, систем уравнений
Замечание. Если на промежутке X функция 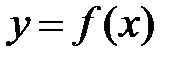 монотонная (возрастает или убывает), то уравнение
монотонная (возрастает или убывает), то уравнение 
 на промежутке X имеет не более одного корня.
на промежутке X имеет не более одного корня.
43. Решите уравнение 
Решение. 1) Рассмотрим левую часть исходного уравнения. Так как функция  возрастает, то
возрастает, то

Итак, левая часть исходного уравнения меньше нуля.
2) Рассмотрим правую часть исходного уравнения. Имеем

Итак, правая часть исходного уравнения не меньше 0,75.
Из 1) и 2) следует, что исходное уравнение корней не имеет.
Ответ. Корней нет.
44. Найдите все значения параметра а, при которых имеет решение уравнение 
Решение. Очевидно, ОДЗ уравнения:  .
.
Перепишем исходное уравнение в виде
 (1)
(1)
Замечание. Функция  возрастает, если
возрастает, если  .
.
Обозначение:  наименьшее значение функции
наименьшее значение функции  на промежутке
на промежутке 
 Если
Если  то исходное уравнение принимает вид
то исходное уравнение принимает вид  Функция
Функция  возрастает на промежутке
возрастает на промежутке  как сумма четырёх возрастающих функций. Так как функция
как сумма четырёх возрастающих функций. Так как функция  возрастает, то
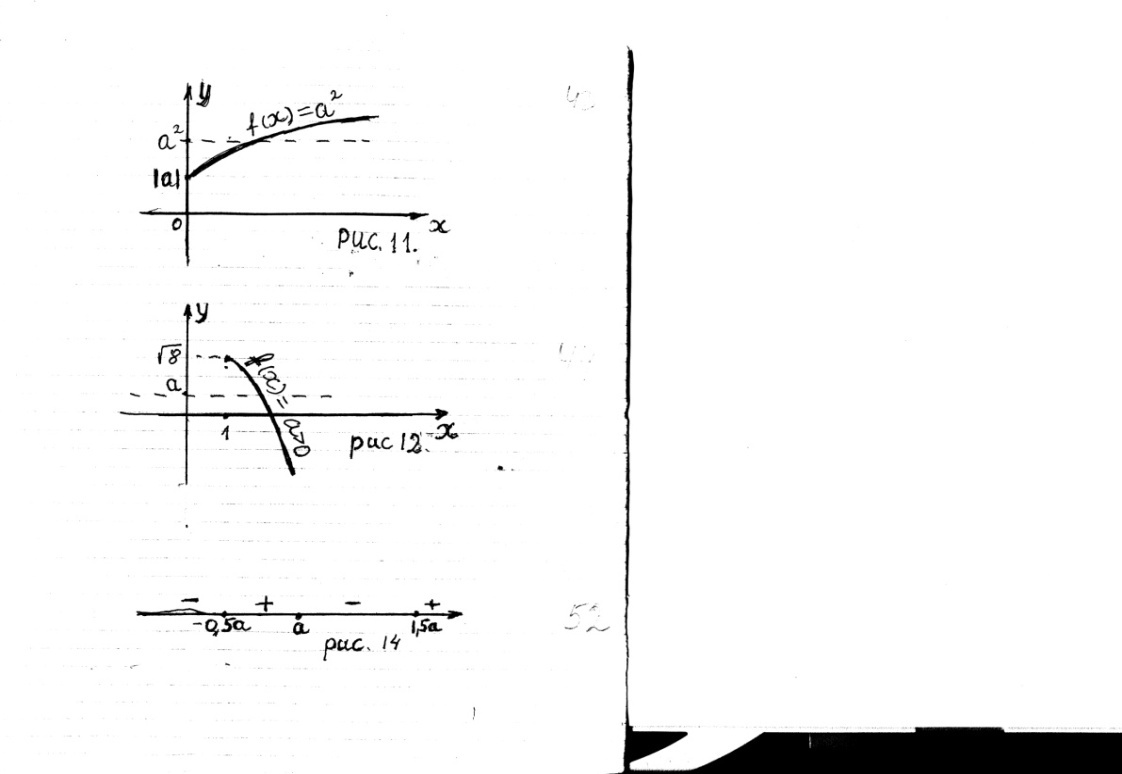
возрастает, то  Тогда уравнение (1) имеет единственный корень (рис. 11), если
Тогда уравнение (1) имеет единственный корень (рис. 11), если

Из последней совокупности следует, что исходное уравнение имеет один корень, если 
Ответ. Один корень, если 
45. Найдите все значения параметра а, при которых имеет решение уравнение 
Решение. ОДЗ уравнения определяется системой неравенств
 Итак, ОДЗ исходного уравнения является промежуток
Итак, ОДЗ исходного уравнения является промежуток 
Преобразуем исходное уравнение

Исходное уравнение равносильно уравнению

Если  то исходное уравнение принимает вид
то исходное уравнение принимает вид  Так как
Так как  то уравнение
то уравнение  может иметь корень, только в случае, если
может иметь корень, только в случае, если 
Замечание. Функции  возрастают, так как производные этих функций положительные.
возрастают, так как производные этих функций положительные.
Так как функции  возрастают, если
возрастают, если  то функция
то функция  возрастает, если
возрастает, если  как сумма возрастающих функций. Тогда функция
как сумма возрастающих функций. Тогда функция  убывает на промежутке
убывает на промежутке  .
.
Обозначение:  наибольшее значение функции
наибольшее значение функции  на промежутке
на промежутке 
 Так как функция
Так как функция  убывает на промежутке
убывает на промежутке  то
то  Тогда уравнение (1) имеет единственный корень (рис.12), если
Тогда уравнение (1) имеет единственный корень (рис.12), если 
Ответ. Один корень, если 
46. Найдите все значения параметра а, при каждом из которых уравнение 
имеет 1) три корня; 2) четыре корня.
Решение. ОДЗ параметра определяется неравенством

1. Так как  и
и  то правая часть уравнения (1) положительная при любом
то правая часть уравнения (1) положительная при любом  .
.
Левая часть уравнения (1) будет положительной, если 
Из неравенства (2) и из неравенства  следует: уравнение (1) может иметь решение, если параметр а удовлетворяет неравенству
следует: уравнение (1) может иметь решение, если параметр а удовлетворяет неравенству 
Пусть  где
где  ,
,  где
где  . Если
. Если 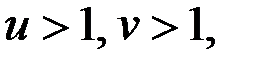 то уравнение (1) принимает вид
то уравнение (1) принимает вид
 Рассмотрим функцию
Рассмотрим функцию  где
где  Функция
Функция  возрастает на интервале
возрастает на интервале  , как произведение двух положительных возрастающих функций. Уравнение (1) принимает вид
, как произведение двух положительных возрастающих функций. Уравнение (1) принимает вид  где
где 
Замечание. Если на промежутке X функция 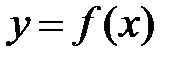 возрастает или убывает, то на этомпромежутке
возрастает или убывает, то на этомпромежутке  .
.
2. Так как функция  , где
, где  возрастает, то уравнение
возрастает, то уравнение  где
где  равносильно системе
равносильно системе

Рассмотрим уравнение 
Пусть  где
где 
 .
.
Так как  постоянная, то уравнение
постоянная, то уравнение  где
где  задаёт семейство прямых, параллельных оси абсцисс.
задаёт семейство прямых, параллельных оси абсцисс.
График функции  получается из графика функции
получается из графика функции  следующим образом:
следующим образом:
а) строим график  ;
;
б) те точки графика, для которых  , остаются без изменения, а точки графика, для которых
, остаются без изменения, а точки графика, для которых  отображаются относительно оси х.
отображаются относительно оси х.
На рисунке 13 изображён график функции  а также графики
а также графики
представителей семейства  .
.
3. Уравнение 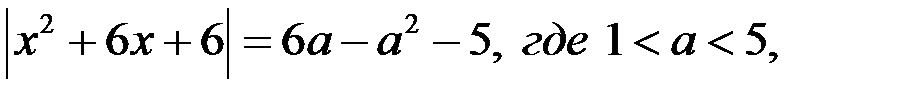 имеет три корня при тех значениях параметра а, при которых графики функций
имеет три корня при тех значениях параметра а, при которых графики функций 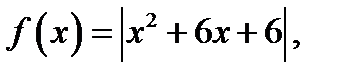
 пересекаются в трёх точках (при этих значениях параметра уравнение (1) также имеет три корня).
пересекаются в трёх точках (при этих значениях параметра уравнение (1) также имеет три корня).
 Прямая
Прямая  , где
, где  , пересекает график функции
, пересекает график функции  в трёх точках (следует из рисунка 13), если прямая
в трёх точках (следует из рисунка 13), если прямая  проходит через точку
проходит через точку  , то есть, если
, то есть, если

Итак, если  то (1) уравнение имеет три разных корня.
то (1) уравнение имеет три разных корня.
4. Уравнение 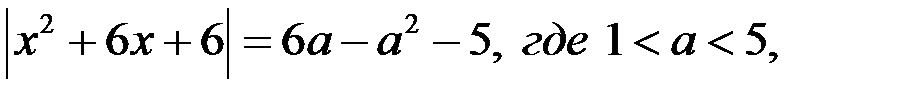 имеет четыре корня при тех значениях параметра а, при которых графики функций
имеет четыре корня при тех значениях параметра а, при которых графики функций 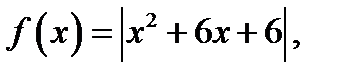
 пересекаются в четырёх точках (при этих значениях параметра уравнение (1) также имеет четыре корня).
пересекаются в четырёх точках (при этих значениях параметра уравнение (1) также имеет четыре корня).
Прямая  , где
, где  , пересекает график функции
, пересекает график функции
 в четырёх точках (следует из рисунка 13), если
в четырёх точках (следует из рисунка 13), если

Итак, если  , то исходное уравнение имеет четыре разных корня.
, то исходное уравнение имеет четыре разных корня.
Ответ. Три корня, если 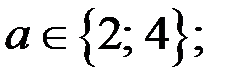
четыре корня, если  .
.
47. Найдите все значения параметра а, при каждом из которых число корней уравнения  не больше числа корней уравнения
не больше числа корней уравнения 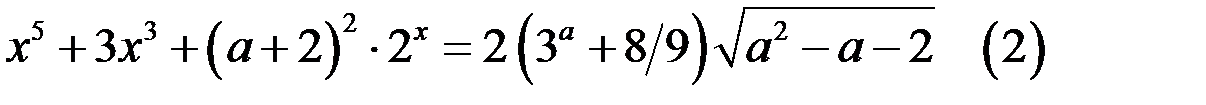
Решение. 1. Рассмотрим уравнение (2).
ОДЗ параметра является множество 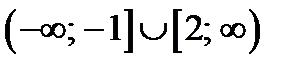 (находится из неравенства
(находится из неравенства  ).
).
Пусть  . Функция
. Функция  возрастает на интервале
возрастает на интервале 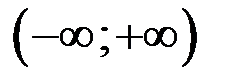 как сумма трёх возрастающих функций. Так как правая часть уравнения (2) является постоянное число, то уравнение (2) принимает вид
как сумма трёх возрастающих функций. Так как правая часть уравнения (2) является постоянное число, то уравнение (2) принимает вид  (С – постоянное число). Тогда уравнение (2) имеет не более одного корня (имеет один корень или не имеет корней).
(С – постоянное число). Тогда уравнение (2) имеет не более одного корня (имеет один корень или не имеет корней).
2. Рассмотрим уравнение (1). Имеем

Уравнение (1) равносильно квадратному уравнению (3). Из условия задачи следует, что число корней уравнения (3) не больше числа корней уравнения  , которое имеет не более одного корня. Тогда и квадратное уравнение (3) должно иметь не более одного корня.
, которое имеет не более одного корня. Тогда и квадратное уравнение (3) должно иметь не более одного корня.
Найдём дискриминант квадратного уравнения (3). Имеем

Имеем  Так как
Так как  то квадратное уравнение (3) при любом значении параметра а имеет корни. Условию задачи могут удовлетворять значения параметра а, при которых
то квадратное уравнение (3) при любом значении параметра а имеет корни. Условию задачи могут удовлетворять значения параметра а, при которых 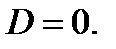
Если  то
то  Если
Если  то уравнение (1) имеет один корень кратности 2.
то уравнение (1) имеет один корень кратности 2.
3. Рассмотрим уравнение (2), если 
1) Так как  не принадлежит ОДЗ параметра уравнения (2), то это уравнение не имеет корней, а уравнение (1) имеет корень. Значит,
не принадлежит ОДЗ параметра уравнения (2), то это уравнение не имеет корней, а уравнение (1) имеет корень. Значит,  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
2) Если  то уравнение (2) принимает вид
то уравнение (2) принимает вид  . Это уравнение имеет единственный корень, так как функция
. Это уравнение имеет единственный корень, так как функция  возрастает. Легко проверить, что единственным корнем уравнения
возрастает. Легко проверить, что единственным корнем уравнения  является
является  Уравнение (1), если
Уравнение (1), если  так же имеет единственный корень. Это означает, что
так же имеет единственный корень. Это означает, что  удовлетворяет условию задачи.
удовлетворяет условию задачи.
Ответ. 
48. Решитеуравнение  .
.
Замечание. Если функция  возрастает, то
возрастает, то 
 .
.
Решение. 1. Если  , то
, то  , где
, где  .
.
Если 
 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид  . Так
. Так
как функция 
 возрастает, то уравнение (1) равносильно уравнению
возрастает, то уравнение (1) равносильно уравнению  , где
, где  .
.
Найдём корни уравнения (2). Имеем

Уравнение (1), а значит и исходное уравнение, может иметь корни, если 
2. Найдём, при каких значениях  , для
, для  выполняется условие
выполняется условие 
1) Рассмотрим двойное неравенство

Итак, если  , то
, то 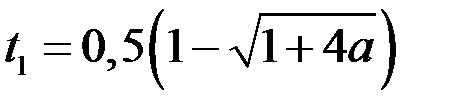 является корнем уравнения (1).
является корнем уравнения (1).
Найдём корень исходного уравнения. Имеем

Итак,  , где
, где  , является корнем исходного уравнения.
, является корнем исходного уравнения.
2) Рассмотрим двойное неравенство

Итак, если  , то
, то  является корнем уравнения (1).
является корнем уравнения (1).
Найдём корень исходного уравнения. Имеем

Итак,  , где
, где  является корнем исходного уравнения.
является корнем исходного уравнения.
Отметим:  если
если 
 если
если  Так как
Так как
функция  возрастает, то
возрастает, то 
Ответ. Нет корней, если  .
.
 , если
, если 
 ,
,  , если
, если 
49. Найдите все значения параметра а, при которых имеет решение
неравенство 
Решение. Очевидно, ОДЗ параметра:  .
.
Замечание. Функция  возрастает, если
возрастает, если  .
.
Перепишем неравенство (1) в виде 
Пусть  .
.
Тогда неравенство (2) принимает вид 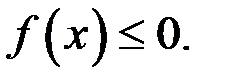
Рассмотрим неравенство (2) и функцию  при различных значениях параметра
при различных значениях параметра  .
.
1) Если  то ОДЗ неравенства (2) определяется системой
то ОДЗ неравенства (2) определяется системой

Если  то ОДЗ неравенства (2) является промежуток
то ОДЗ неравенства (2) является промежуток 
Так как функция  возрастает на промежутке
возрастает на промежутке  то
то 
Неравенство (2) имеет решение, если
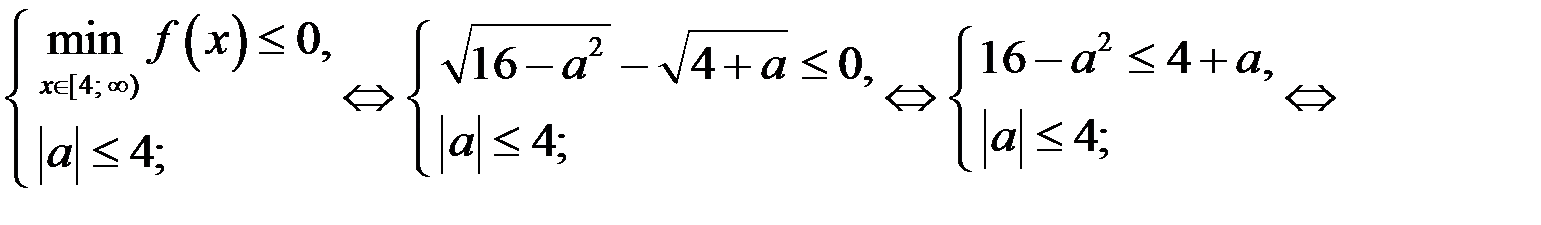

Из последней совокупности следует, что исходное неравенство имеет решение, если 
2) Если  то ОДЗ неравенства (2) определяется системой
то ОДЗ неравенства (2) определяется системой

Если  то ОДЗ неравенства (2) является промежуток
то ОДЗ неравенства (2) является промежуток 
Так как функция  возрастает на промежутке
возрастает на промежутке  то
то 
Неравенство (2) имеет решение, если

Итак, исходное неравенство имеет решение, если 
Ответ. 
50. Найдите все значения параметра а, при которых имеет единственное решение неравенство  (1).
(1).
Решение. 1. Очевидно,  .
.
Сделаем замену  , где
, где  . Исходное неравенство принимает вид
. Исходное неравенство принимает вид 
2. Если  то
то  Тогда неравенство (2) равносильно неравенству
Тогда неравенство (2) равносильно неравенству 
Пусть 
Функция  , где
, где  , возрастает, как сумма двух возрастающих функций. Неравенство (3) принимает вид
, возрастает, как сумма двух возрастающих функций. Неравенство (3) принимает вид 
Так как функция  , где
, где  , возрастает, то уравнение
, возрастает, то уравнение  , где
, где  , имеет не более одного корня. Очевидно,
, имеет не более одного корня. Очевидно,  .
.
Тогда имеем
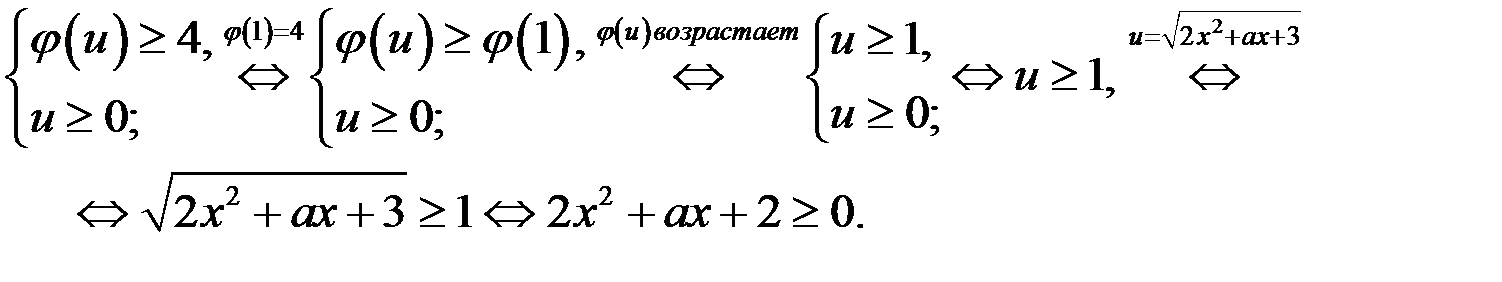
Так как дискриминант уравнения  равный
равный  ,
,
отрицательный, если  , то решениями неравенства
, то решениями неравенства 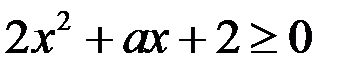
являются  . Поэтому для любого
. Поэтому для любого  неравенство (1) имеет бесконечное множество решений.
неравенство (1) имеет бесконечное множество решений.
3. Если 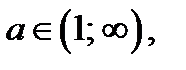 то
то  Неравенство (2) равносильно неравенству
Неравенство (2) равносильно неравенству  Тогда имеем
Тогда имеем


Рассмотрим систему (4).
Дискриминант уравнения  равен
равен  .
.
а) Пусть 
Уравнение  , если
, если  , имеет единственное решение, если
, имеет единственное решение, если
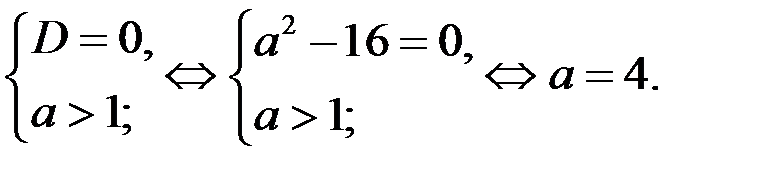
Если  , то система (4) принимает вид
, то система (4) принимает вид

Итак, если  , то система (4), а значит и исходное неравенство, имеет единственное решение.
, то система (4), а значит и исходное неравенство, имеет единственное решение.
б) Если  то первое неравенство системы (4) не имеет решений. Тогда система (4), а значит и исходное неравенство, не имеет решений.
то первое неравенство системы (4) не имеет решений. Тогда система (4), а значит и исходное неравенство, не имеет решений.
в) Пусть 
Уравнение  , если
, если  , имеет два корня, если
, имеет два корня, если

Множеством решений первого неравенство системы (4), если  , является отрезок
, является отрезок  где
где  корни уравнения
корни уравнения 
Докажем, что неравенство  если
если  , имеет не менее двух решений.
, имеет не менее двух решений.
Если  , являются решениями уравнения
, являются решениями уравнения 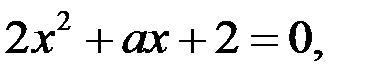 то
то
 Тогда
Тогда 
Итак, если  , то система (4), значит и неравенство (1), имеет не менее двух решений.
, то система (4), значит и неравенство (1), имеет не менее двух решений.
Ответ.  .
.
51. Решите систему уравнений 
Решение. 1. Система (1) равносильна системе уравнений

Рассмотрим первое уравнение системы (2).
Пусть  . Эта функция возрастает, как сумма возрастающих функций. Тогда уравнение
. Эта функция возрастает, как сумма возрастающих функций. Тогда уравнение  (первое уравнение системы (2)) равносильно уравнению
(первое уравнение системы (2)) равносильно уравнению  .
.
Получили, что система (2) равносильна системе
 2. Рассмотрим второе уравнение системы (3). Имеем
2. Рассмотрим второе уравнение системы (3). Имеем


Определим, при каких значениях параметра а числа 
 удовлетворяют неравенству
удовлетворяют неравенству 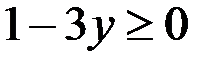 .
.
а) Число  удовлетворяет неравенству
удовлетворяет неравенству 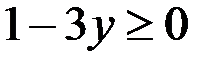 , если
, если

Итак, если  , то
, то  является решением уравнения
является решением уравнения  .
.
б) Число  удовлетворяет неравенству
удовлетворяет неравенству 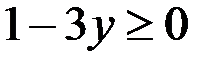 , если
, если

Так как последняя система не имеет решений, то  ни при каких значениях параметра а не является решением уравнения
ни при каких значениях параметра а не является решением уравнения  .
.
3. Найдём решение системы (3), значит и системы (1).
Если  , то
, то  является решением второго уравнения системы. Тогда из первого уравнения системы (3) находим
является решением второго уравнения системы. Тогда из первого уравнения системы (3) находим  .
.
Ответ. Если  то
то  ;
;
если  то решений нет.
то решений нет.
Критические точки.Экстремумы
Внутренняя точка области определения функции, в которой производная равна нулю или не существует, называется критической.
Точка  является точкой максимума (минимума) функции
является точкой максимума (минимума) функции 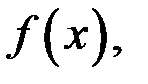 если существует такая окрестность точки
если существует такая окрестность точки  , что
, что
1)функции  является непрерывной в этой окрестности;
является непрерывной в этой окрестности;
2) производная функции при переходе через точку  в этой окрестности меняет знак с плюса на минус (с минуса на плюс).
в этой окрестности меняет знак с плюса на минус (с минуса на плюс).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции обозначают 
 .
.
Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках называются экстремумами.
52. Найдите критические точки и точки экстремумов функции 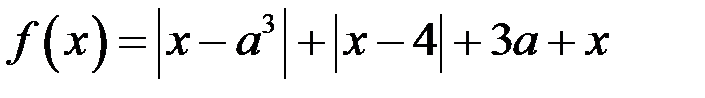 .
.
Решение. 
Рассмотрим различное расположение точки  относительно точки
относительно точки  .
.
1. Если  , то исходная функция принимает вид
, то исходная функция принимает вид

Найдём производную функции (1), если  . Имеем
. Имеем
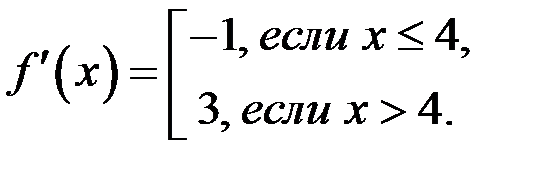
В точке  функция (1) не имеет производной. Поэтому точка
функция (1) не имеет производной. Поэтому точка  является критической, если
является критической, если  .
.
При переходе через точку  производная функции (1), меняет знак с минуса на плюс, поэтому точка
производная функции (1), меняет знак с минуса на плюс, поэтому точка  , если
, если  . является точкой минимума.
. является точкой минимума.
2. Если  , то
, то

Найдём производную функции (2), если  . Имеем
. Имеем

В точке  функция (2) не имеет производной. Поэтому точка
функция (2) не имеет производной. Поэтому точка  является критической, если
является критической, если  . Так как при переходе через точку
. Так как при переходе через точку  производная функции (2) меняет знак с минуса на плюс, то точка
производная функции (2) меняет знак с минуса на плюс, то точка  является точкой минимума (точка экстремума), если
является точкой минимума (точка экстремума), если  .
.
В точке  функция (2) не имеет производной. Поэтому точка
функция (2) не имеет производной. Поэтому точка  является критической, если
является критической, если  . При переходе через точку
. При переходе через точку  производная функции (2) не меняет знак, поэтому точка
производная функции (2) не меняет знак, поэтому точка  не является точкой экстремума.
не является точкой экстремума.
3. Если  , то
, то

Найдём производную функции (3), если  . Имеем
. Имеем

В точке  функция (3) не имеет производной. Поэтому точка
функция (3) не имеет производной. Поэтому точка  является критической, если
является критической, если  . При переходе через точку
. При переходе через точку  производная функции (2) меняет знак с минуса на плюс, поэтому точка
производная функции (2) меняет знак с минуса на плюс, поэтому точка  является точкой минимума (точка экстремума), если
является точкой минимума (точка экстремума), если  .
.
В точке  функция (3) не имеет производной. Поэтому точка
функция (3) не имеет производной. Поэтому точка  является критической, если
является критической, если  . При переходе через точку
. При переходе через точку  производная функции (2) не меняет знак, поэтому точка
производная функции (2) не меняет знак, поэтому точка  не является точкой экстремума.
не является точкой экстремума.
Ответ. Если  то точки
то точки  и
и  являются критическими; если
являются критическими; если  , то точка
, то точка  является критической; если
является критической; если 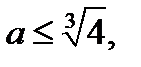 то точка
то точка  является точкой экстремума; если
является точкой экстремума; если  , то
, то
точка  являетсяточкой экстремума.
являетсяточкой экстремума.
53. Найдите то