В случае аналитического сглаживания фактические уровни ряда заменяются теоретическими, рассчитанными по определенной кривой, отражающей общую тенденцию изменения показателя во времени. Эти кривые получили название кривых роста. Существует большое количество кривых роста (трендовых моделей), которые описывают временной ряд.
Наиболее часто используются:
· Полиномиальные;
· Экспоненциальные;
· S-образные кривые.
Полиномиальные кривые используются для приближения (аппроксимации) и прогнозирования временных рядов, в которых последующее развитие не зависит от достигнутого уровня.
В отличие от полиномиальных моделей, использование моделей экспоненциальных предполагает, что дальнейшее развитие зависит от достигнутого уровня.
В экономике распространены процессы, которые сначала растут медленно, затем ускоряются, затем снова замедляют свой рост и т.д.
S-образные кривые применяются для описания именно этих процессов.
Аналитическое сглаживание: Метод характеристик прироста.
При этом методе исходный временной ряд предварительно сглаживается методом простой скользящей средней
Но чтобы не потерять первый и последный уровни, для них рекомендуется:
Затем вычисляются первые средние приросты 
, вторые средние приросты 
, а также ряд производных величин, связанными с вычисленными средними приростами и сглаженными уровнями ряда: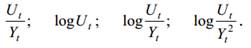 
.
В соответствии с найденными показателями и соотношениями выбирается вид кривой роста для исходного временного ряда.
На практике при предварительном выборе отбирают несколько кривых роста для дальнейшего исследования и построения трендовой модели данного временного ряда.
Для выбора вида полиномиальной кривой используется метод конечных разностей или метод Тинтнера.
Ограничения метода Тинтнера:
- уровни временного ряда состоят только из двух компонент: тренд и случайная компонента.
-тренд является достаточно гладким, чтобы его можно было приближать (аппроксимировать) к полиному.
Как работает метод:
1. Вычисляются разности до 
порядка включительно.
и т.д. до 
порядка включительно.
Обычно вычисляются конечные разности до 4-ого порядка включительно.
2. Затем вычисляется дисперсия:
3. Далее производится сравнение отклонений каждой последующей дисперсии от предыдущей.
Если эти величины меньше некоторой наперед заданной положительной величины, то степень полинома должна быть равна 
После того, как модель выбрана, и ее параметры оценены, мы должны:
Проверить модель на адекватность .
Независимо от вида и способа построения трендовой модели возможность её применения для анализа и прогнозирования может быть решена только после проверки её адекватности и точности. Трендовая модель считается адекватной, если правильно отражает систематические компоненты временного ряда.
Эти требования эквивалентны следующему требованию:
Остаточная компонента (случайная): 
(исходный временной ряд минус найденная модель – ряд остатков) должна отвечать (соответствовать) следующим условиям (свойствам):
1) Случайность колебаний уровней (
- случайная величина)
2) Соответствие распределения случайной компоненты нормальному закону распределения
( - подчиняется нормальному закону распределения)
3) Равенство математического ожидания случайной компоненты нулю
(
– при 2-ом условии = 0)
4) Независимость значений уровней случайной компоненты (отсутствие автокорреляции)
(уровни – независимые, т.е. внутренняя корреляция отсутствует)
Свойство №1. О случайность колебаний уровней.
I. Критерий серий
Основан на медиане выборки: 
- медиана выборки
(Расставить ряд в порядке возрастания и найти середину)
Создается новый ряд, состоящий, в основном из + и –:
Если > => 
Если < => 
Если = => 
Получаем серии из плюсов и минусов. Один + => серия количества 1, затем считаем количество серия и обозначаем
Выбираем серию максимальной длины, и обозначаем как K max.
Чтобы модель считалась адекватной и верной, должно выполняться:
Если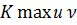 
соответствуют условиям, то с вероятностью 
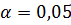наша выборка считается случайной, т.е. гипотеза о случайности выбранных данных будет иметь место.
Если хотя бы одно из условий 
будет нарушено, модель считается неверной, неадекватной.
II. Критерий поворотных точек (критерий пиков).
Каждый элемент ряда 
сравниваем с двумя соседними значениями . Если , больше, чем 
и 
, то считается максимумом (+).Если , меньше, чем и , то считается максимумом (-).
И в том и в другом случает значение , отличное от других, является поворотной точкой. Общее количество поворотных точек (min и max) обозначается как 
.
Математическое ожидание числа поворотных точек определяется по таблице или по формуле: 
.
Дисперсия числа поворотных точек определяется, также, по таблице или по формуле: 
При 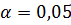проверяется следующее условие: 
. Если это условие выполняется, то считается, что выборка случайная и 1ое условие выполнилось, иначе – выборка не случайная и модель не адекватна.
Свойство №2. Проверка соответствия распределения случайной компоненты нормальному закону распределения.
1ый способ. Это свойство может проверяться с помощью показателей асимметрии и эксцесса.
Находятся коэффициенты асимметрии и эксцесса для ряда . Затем для этих коэффициентов находятся дисперсии по формулам:
А далее должно выполняться следующее условие:
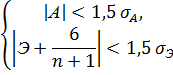
Если это условие выполняется, то второе свойство верно и распределение случайной компоненты соответствует нормальному закону распределения.
Если же 
, модель не адекватна.
2ой способ. Также свойство №2 может проверяться с помощью критерия согласия 
.
Последовательность действий:
1. Разбиваем 
на группы по формуле: 
, где 
, соответственно, количество групп (но чаще всего количество групп принимается равным 6, для упрощения расчетов).
2. Находим размах вариации: 
и длину интервала: 
,
3. Затем разбиваем нашу выборку на интервалы:
и т.д. до
4. После разбиения выборки на интервалы считаем количество значений , попадающих в интервалы 
(или 
так, чтобы 
.
5. Находим вероятность попадания значений в 
, при этом считаем, что 
Т.к. мы проверяем нормальное распределение, то берем вместо 
функцию нормального распределения:
После того, как мы нашли все вероятности попадания в интервалы нужно проверить условие: 
. Если это условие не выполняется, нужно объединять соседние интервалы так, чтобы это условие выполнилось.
6. Затем находим критерий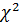 
:
При заданном уровне значимости 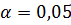и числом степеней свободы 
находим 
и сравниваем его с 
.
Если 
, то основная гипотеза принимается, распределение случайной компоненты соответствует нормальному закону распределения.
Свойство №3. О равенстве математического ожидания случайной компоненты нулю.
Критерий Стьюдента.
1. Находим значение показателя 
по формуле:
2. При заданном уровне значимости 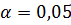и числом степеней свободы находим 
.
Если 
, то гипотеза о равенстве математического ожидание случайной компоненты принимается, иначе – отвергается и выбранная модель считается неадекватной.
Свойство №4. Об отсутствии автокорреляции (уровни между собой не зависят).
Корреляционная зависимость между рядом наблюдений и тем же рядом, сдвинутым во времени на несколько шагов, называется автокорреляцией.