Лабораторная работа
Состояния микрочастицы в прямоугольной потенциальной яме
Цель работы: Определить функции состояния и возможные значения энергии микрочастицы, находящейся в прямоугольной одномерной потенциальной яме.
Теоретическое введение
Теорией, объясняющей основные свойства атомных и ядерных явлений, является квантовая механика, начало которой было положено работами де Бройля, Бора, Шредингера, Гейзенберга, Борна, Дирака, Паули, Ферми и др. Квантовая механика является теорией, лежащей в основе объяснения свойств атомов, молекул, атомных ядер, т.е. явления, происходящие в системах, линейные размеры которых порядка 10-6 – 10-13 см.
Основным уравнением квантовой механики в нерелятивистском приближении является уравнение Шредингера. Стационарное уравнение Шредингера для частицы массой m в потенциальном поле U имеет вид:
. (1)
Решением уравнения Шредингера в общем случае является функция состояния Ψ, квадрат модуля которой имеет смысл плотности вероятности найти частицу в объеме dτ около точки с координатами x, y, z. Сама же вероятность пропорциональна Ψ*Ψdτ.
Функция Ψ по своему смыслу должна удовлетворять некоторым стандартным условиям: она должна быть во всем пространстве конечной непрерывной и однозначной функцией, ее первые производные по координатам должны быть также непрерывны. Для нее справедливо условие нормировки:
. (2)
Решения удовлетворяют этим требованиям при вполне определенных условиях, например, при определенных дискретных значениях энергии, входящей в качестве параметра в уравнение (1).
Рассмотрим простейшие случаи движения микрочастиц.
1. Бесконечно глубокая потенциальная яма.
Рассмотрим состояния частицы, находящейся в одномерной прямоугольной бесконечно глубокой потенциальной яме. Потенциальная энергия частицы в зависимости от координаты x изображена на рисунке 1. При 0< x < a потенциальную энергию частицы можно принять равной нулю, а вне этого интервала она обращается в бесконечность. Вследствие этого частица при своем движении не может выйти за пределы (0, а). Поскольку вероятность нахождения частицы вне интервала (0, a) равна нулю, то и Ψ - функция вне этого интервала равна нулю. А так как она должна быть непрерывной функцией во всей области
 |
координат, то в точках x=0 и x=a она обращается в нуль. Таким образом, для функции Ψ(x) получаются следующие граничные условия:
Ψ(0)=Ψ(а)=0
Уравнение Шредингера внутри ямы, где потенциальная энергия равна нулю, имеет вид
(3)
где принято обозначение
(4)
Общее решение этого уравнения таково
Граничное условие Ψ(0)=0 дает B=0, а из граничного условия Ψ(а)=0 следует что
аχ=nπ, (5)
где n=1,2,3,…
На основании соотношений (4) и (5) получаем выражение для уровней энергии
. (6)
Это условие квантует энергию частицы. Формула (6) показывает, что существует некоторая минимальная энергия, не равная нулю, соответствующая состоянию движения частиц.
Волновая функция этого состояния
ни в какой точке интервала (0, а) не обращается в нуль. Свойство волновой функции имеет общий характер: волновая функция основного состояния не имеет узлов, т.е. не обращается в нуль внутри рассматриваемой области, а может обращаться в нуль только на границах.
Из формулы (6) видно, что при увеличении линейного размера ямы минимальная энергия уменьшается. Физическая причина состоит в том, что при уменьшении размеров ямы уменьшается длина волны де-Бройля, а уменьшение длины волны означает увеличение энергии частицы.
Поскольку спектр дискретен, условие нормировки
для нормировочного множителя дает
.
Поэтому система собственных функций имеет вид:
. (7)
2. Одномерная яма конечной глубины
Рассмотрим состояния частицы в потенциальном поле, где при 
потенциальная энергия равна U1, при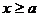 
потенциальная энергия принимает значение U2, а в интервале 
она обращается в нуль (смотри рисунок 2).
Т.к. значения энергий конечны, то частица может находиться в любой области. Поэтому нужно найти волновую функцию в трех областях.
Уравнения Шредингера во всех трех областях имеют вид:
, где 
, где 
, где 
рассмотрим случай, когда значение полной энергии частицы удовлетворяет условию: U1>U2>E.
Решения уравнений Шредингера для всех областей будет иметь вид:
для : 
для : 
для :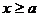 
.
Из условий непрерывности Ψ и ее производной на границах ямы вытекает условие
,
откуда получаем
.
Здесь α – некоторая постоянная. Исключив из этих уравнений α, получим выражение:
, (8)
где n=1,2,3,…, а значения arcsin берутся в интервале (0, π/2). Решения данного уравнения и представляет собой дискретный спектр собственных значений E.
Решение данной задачи можно осуществить системе Mathcad, для чего составлена соответствующая программа. При изменении значений параметров, программа автоматически вычисляет новые значения функций.
Например, для электрона в яме шириной 10-9м и высотой барьеров U1=6 эВ и U2=8 эВ, уравнение имеет четыре решения, т.е. только четыре уровня энергии “помещаются” в яму (смотри рисунок 3). Значения энергий таковы:
 |
Соответствующие функции состояния имеют вид, показанный на рисунке 4.
 |
Порядок выполнения работы
1. Изучить стационарное и нестационарное уравнения Шредингера.
2. Ознакомиться с алгоритмом решения уравнения Шредингера.
3. Задать конкретные значения ширины и глубины асимметричной потенциальной ямы и получить решения для собственных функций и собственных значений оператора энергии. Представить их в графическом виде.
4. Повторить п.3 для 2-3 наборов параметров потенциальной ямы.
5. Проанализировать влияние численных значений ширины и глубины потенциальной ямы на решение уравнения Шредингера.
Контрольные вопросы
1. Каким требованиям удовлетворяет основное уравнение квантовой механики в нерелятивистском приближении?
2. Записать стационарное и нестационарное уравнения Шредингера.
3. Статистическая интерпретация решений уравнения Шредингера, стандартные условия.
4. Решение стационарного одномерного уравнения Шредингера для частицы в прямоугольной потенциальной яме бесконечной глубины.
5. Анализ полученных решений.