Самостоятельная работа « Построение двух графиков в одной системе координат»

Построить в одной системе координат графики следующих двух функций:

y = 2sin(x) и z = 3cos(2x) – sin(x) при x Î [-3;3]

В ячейки A2:A17 вводим значения переменной x от –3 до 3 с шагом 0,2. В ячейки B1 и C1 вводим y и z соответственно, а в ячейки B2 и C2 – формулы:

= 2*sin(A2)

=3*cos(2*A2) – sin(A2)

Выделим диапазон B2:C2, установим указатель мыши в его правом нижнем углу и с помощью автозаполнения скопируем формулы в ячейки B3:C32.

Выделим диапазон ячеек A1:C32, вызовем Мастер диаграмм. Выберем тип диаграммы – Точечная и вид графика. На втором шаге Мастера диаграмм в группе Ряды данных установим переключатель в положение В столбцах. На третьем шаге Мастера диаграмм в поле Название диаграммы вводим Графики функций, в поле Ось x – x, в поле Ось y – y и z. Нажатие кнопки Готово завершает построение графиков (Рис.4.14).

Рис. 4.14. График двух функций в одной системе координат

Графики функций y и zмогут для наглядности различаться по типу линий. Для этого график, внешний вид которого мы хотим изменить, выделяется и с помощью Контекстного меню вызывается диалоговое окно Форматирование элемента данных, которое позволяет изменять тип, толщину и цвет линии, а также тип, цвет и фон маркера.

Самостоятельная работа «Нахождение корней уравнения »

Найти все корни уравнения

x³ – 0.01x² – 0.7044x + 0.1391 = 0

У полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно нужно локализовать, т.е. определить интервалы, на которых они расположены. С этой целью построим график функции

y = x³ – 0.01x² – 0.7044x + 0.1391

на отрезке [-1,1] с шагом 0.1. В столбец А введем значения x, в столбец В – значения y, вычисленные по формуле (рис. 4.15):

= A2^3 – 0.01*A2^2 – 0.7044*A2 + 0.1391

Рис. 4.15. Локализация корней полинома

 

Из рисунка видно, что полином меняет знак на интервалах: [-1, -0.8], [0.2, 0.3], [0.7, 0.8]. Это значит, что на каждом из них имеется корень данного уравнения. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни. Найдем их методом последовательных приближений с помощью команды Сервис/ Подбор параметра. Но, прежде всего, зададим относительную погрешность и предельное число итераций равными, например, 0.0001 и 1000. Эти параметры Excel задаются с помощью команды Сервис/ Параметры – на вкладке Вычисления (рис. 4.16).

Рис.4.16. Вкладка Вычисления диалогового окна Параметры

В качестве начальных приближений можно взять любые точки из отрезков локализации корней, например, точки: -0.95, 0.25 и 0.75. Введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу:

= C2^3 – 0.01*C2^2 – 0.7044*C2 +0.1391

Выделим эту ячейку и, с помощью маркера заполнения распространим введенную в нее формулу на диапазон D2:D4. Таким образом, в ячейках D2:D4 вычисляются значения полинома при значениях аргумента, введенного в ячейки C2:C4 соответственно. Теперь выберем команду Сервис/Подбор параметра и заполним диалоговое окно Подбора параметра (рис. 4.17)следующим образом.

Рис. 4.17. Диалоговое окно Подбор параметра

 

В поле Установить в ячейке введем D2. Отметим, что в этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. Для нахождения корня уравнения с помощью подбора значения параметра, надо записать уравнение так, чтобы его правая часть не содержала переменную.

В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную). Вводить ссылки на ячейки в поля диалогового окна Подбор параметра удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере $D$2, $C$2).

После нажатия кнопки OKпроцедура подбора параметров находит приближенное значение корня, которое помещает в ячейку С2. В данном случае оно равно -0.920. Как выглядит диалоговое окно Результат подбора параметра после завершения поиска решения, показано на рис. 4.18.

Рис. 4.18. Диалоговое окно Результат подбора параметра

Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0.210 и 0.720.

Самостоятельная работа «Решение системы линейных уравнений »

Дана система линейных уравнений:

2х₁+3х₂+7х₃+6х₄=1

3х₁+5х₂+3х₃+х₄=3

5х₁+3х₂+х₃+3х₄=4

3х₁+3х₂+х₃+6х₄=5

Пусть матрица записана в ячейки А10:D13, а свободные члены - в ячейки F10:F13.

В Excel имеются следующие функции для работы с матрицами:

МОБР – обращение матрицы,

МОПРЕД – вычисление определителя матрицы,

МУМНОЖ – матричное произведение двух матриц,

ТРАНСП – транспонирование матрицы.

Решение линейной системы АХ=В, где А - матрица коэффициентов, В - столбец (вектор) свободных членов, Х - столбец (вектор) неизвестных, имеет вид Х=А^-1В, где А^-1 - обратная матрица.

Выделите под вектор решений диапазон G10:G13 и введите формулу: =МУМНОЖ(МОБР(А10:D13); F10:F13)

Для получения решения нажмите < Ctrl>+<Shift>+<Enter>; сделайте проверку решения: в первое уравнения подставьте значения корней.

Самостоятельная работа «Построение уравнения линейной регрессии »

i	xi	yi

Имеются две наблюдаемые величины x и y, например, объем реализации фирмы, торгующей автомобилями, за шесть недель ее работы. Значения наблюдаемых величин приведены в таблице, где x – отчетная неделя, а y – объем реализации за эту неделю.

Необходимо построить линейную модель y=аx+b, которая бы наилучшим образом описывала наблюдаемые значения. Такая модель называется уравнением регрессии. Для его построения определяют коэффициенты а и b так, чтобы минимизировалась некоторая целевая функция. В качестве такой функции обычно выбирают сумму квадратов отклонений заданных значений y_i от соответствующих значений, вычисляемых с помощью уравнения регрессии. Для решения этой задачи в ячейки D3:E3 вводим ориентировочные значения коэффициентов a, b (например, a =2, b =2), а в ячейку F3 (Рис. 4.19) вводим целевую функцию СУММКВРАЗН(C2:C7;E3+D3*B2:B7).

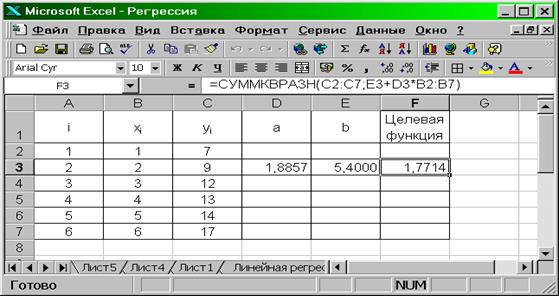Рис. 4.19. Вычисление коэффициентов уравнения регрессии с использованием целевой функции

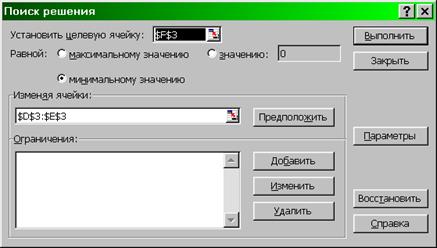Выбираем команду Сервис/Поиск решения и заполняем диалоговое окно Поиск решения (Рис. 4.20).

Рис.4.20. Диалоговое окно Поиск решения

Результат нахождения параметров a и b – на рис. 4.20. Полученное уравнение регрессии: y = 1,8857x + 5,4.

Другой способ получения уравнения линейной регрессии основывается на построении линии тренда. Построим точечный график по диапазону ячеек B2:C7, выделим точки графика двойным щелчком, а затем щелкнем правой кнопкой мыши. В появившемся контекстном меню выберем команду Линии тренда. Выберем Тип/Линейная, а на вкладке Параметры установим флажки: Поместить уравнение на диаграмме, Поместить на диаграмму величину достоверности аппроксимации (R²). На рис. 4.21 – результат построения линии тренда. Коэффициент R² характеризует ту долю дисперсии (изменений) функции y, которая прогнозируется с помощью найденного уравнения регрессии. Этот коэффициент называют ещё коэффициентом детерминации. По его величине судят о том, можно ли использовать уравнение регрессии для прогнозирования.

Рис. 4.21. Построение линии тренда

Для прогноза с помощью уравнения регрессии используется встроенная функция ТЕНДЕНЦИЯ(<известные y >;<известные x >;<новые x >), которая вычисляет ожидаемые новые значения y для новых x, если известны некоторые опытные значения x и y. Вычисления делаются в предположении, что x и y зависят линейно. Вычислите ожидаемый объем реализации автомобилей за 7-ю, 8-ю и 9-ю недели работы фирмы.

В рассматриваемой задаче объем реализации автомобилей (y) был дан за 6 недель (x= 1,2,...,6). Так как результат должен выводиться в три ячейки, значит функция ТЕНДЕНЦИЯ() должна вводиться как функция обработки массива. Выделяется диапазон ячеек C8:C10 (Рис. 4.22), вводится функция ТЕНДЕНЦИЯ() и нажимаются клавиши Ctrl+Shift+Enter (вместо обычного Enter). Результат прогноза виден на рис. 4.22.

Рис.4.22. Вычисление прогнозных значений y с использованием функции ТЕНДЕНЦИЯ

Таким образом, на 7-й неделе работы фирмы ожидается продажа 19-ти машин, на 8-й неделе – продажа 20-ти машин, на 9-й неделе – продажа 22-х машин. При этом надо иметь в виду, что математический прогноз подтвердится только в том случае, если наметившаяся за первые шесть недель тенденция увеличения продаж сохранится ещё в течение трёх недель. Таким образом, математический прогноз может быть успешным только в рамках принятой модели. При изменении ситуации необходимо изменять модель, например, вместо линейного уравнения регрессии использовать параболическое или экспоненциальное.

Самостоятельная работа «Построение математических моделей задач линейного программирования »

Линейное программирование – это раздел прикладной математики, посвященный методам нахождения наибольших или наименьших значений линейной функции многих переменных, т.е. функции вида:

причем переменные x_j (j= 1, 2, …, n) должны удовлетворять дополнительным условиям, имеющим вид линейных уравнений или (и) неравенств:

где a_ij, b_i, c_j (i =1, 2,…, m; j =1, 2, …, n) – заданные постоянные числа.

Обычно в задачах линейного программирования на переменные налагаются еще условия неотрицательности: x_j ³ 0 (j= 1, 2, …, n).

Линейная функция z называется целевой функцией или функцией цели, а дополнительные условия называются ограничениями. Решение задачи линейного программирования состоит в нахождение переменных x_j, которые удовлетворяют системе ограничений и минимизируют (максимизируют) целевую функцию.

Рассмотрим задачу оптимального планирования производства красок на фабрике. Фабрика выпускает два типа красок: для внутренних (I) и наружных (E) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В.

Исходный продукт	Расход исходных продуктов на тонну краски, т	Максимально возможный запас, т
краска Е	краска I
А
В

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более, чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны краски равны: 3000 руб. для краски Е и 2000 руб. для краски I. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Итак, требуется спланировать объем производства красок так, чтобы максимизировать прибыль. Поэтому переменными являются x_I – суточный объем производства краски I и x_Е – суточный объем производства краски Е.

Суммарная суточная прибыль от производства x_I тонн краски I и x_Е тонн краски Е равна z = 3000 x_Е + 2000 x_I. Задача заключается в определении среди всех допустимых значений x_I и x_Е таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z.

 

Налагаем ограничения на x_I и x_Е.

x_I, x_Е >= 0 – объем производства красок не может быть отрицательным.

– ограничения на расход исходного продукта

2x_I + x_Е <=6

x_I + 2 x_Е <=8

– ограничения на величину спроса краски

x_I - x_Е <=1

x_I <=2

В итоге математическая модель имеет следующий вид:

z = 3000 x_Е + 2000 x_I ® max

при следующих ограничениях:

2x_I + x_Е <=6

x_I + 2 x_Е <=8

x_I - x_Е <=1

x_I <=2

x_I, x_Е >= 0

Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.

 

Выполнение работы

На листе Excel создайте таблицу:

 

	A	B	C
	Переменные
	xE	xI
	Функция цели		=3000*A3+2000*B3
	Ограничения
	=A3+2*B3
	=2*A3+B3
	=B3-A3
	=B3

 

Установите курсор в ячейку С4, выполните пункт меню Сервис/Поиск решения. Установите переключатель Равной максимальному значению. В поле Изменяя ячейки укажите ячейки А3:В3.

Для ввода ограничений щелкните по кнопке Добавить, в поле ссылка на ячейку укажитеА7:А10, установите £ и в поле ограничение укажите диапазон В7:В10. Нажмите кнопку Добавить. Введите ограничение: А3:В3 ³ 0. После ввода ограничений щелкните по кнопке ОК.

Нажмите кнопку Параметры и в диалоговом окне установите флажок Линейная модель. Для получения результата щелкните по кнопке Выполнить.

По окончании решения задачи в ячейках листа получите следующие результаты.

	A	B	C
	Переменные
	xE	xI
	3.333333	1.333333
	Функция цели		12666.67
	Ограничения
	-2
	1.333333

 

 

Приведённые в этом пособии лабораторные и самостоятельные работы показывают, сколь широк круг задач, решение которых без особых усилий можно выполнить с помощью электронных таблиц.