Неявные функции и дифференцируемые отображения
Неявные функции
Неявные функции одной и двух переменных. Пусть функция двух переменных  определена на некотором множестве
определена на некотором множестве  плоскости
плоскости  переменных
переменных 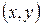 . Тогда, если существует функция
. Тогда, если существует функция  одной переменной
одной переменной  , определенная на множестве
, определенная на множестве  , такая, что
, такая, что  выполняется равенство
выполняется равенство  то, этом случае функция
то, этом случае функция  , называется неявно заданной функцией уравнением
, называется неявно заданной функцией уравнением  .
.
Пусть в трехмерном пространстве  задан цилиндр (рис.5)
задан цилиндр (рис.5)



и в этом цилиндре определена функция  . Тогда, если существует функция
. Тогда, если существует функция  двух переменных
двух переменных 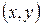 , определенная на множестве
, определенная на множестве  такая, что
такая, что  выполняется равенство
выполняется равенство  , то функция
, то функция  называется неявно заданной функцией уравнением
называется неявно заданной функцией уравнением  .
.

|
Примеры. 1) Уравнение  задает неявно бесконечное множество функций, определенных на
задает неявно бесконечное множество функций, определенных на  (рис.6).
(рис.6).
2)Рассмотрим функцию  . Пусть
. Пусть  – некоторая окрестность точки
– некоторая окрестность точки  , и координаты точки
, и координаты точки  удовлетворяют уравнению
удовлетворяют уравнению  ,
, 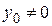 . Тогда существует единственная неявная функция, такая, что ее график содержится в
. Тогда существует единственная неявная функция, такая, что ее график содержится в  (рис.7).
(рис.7).
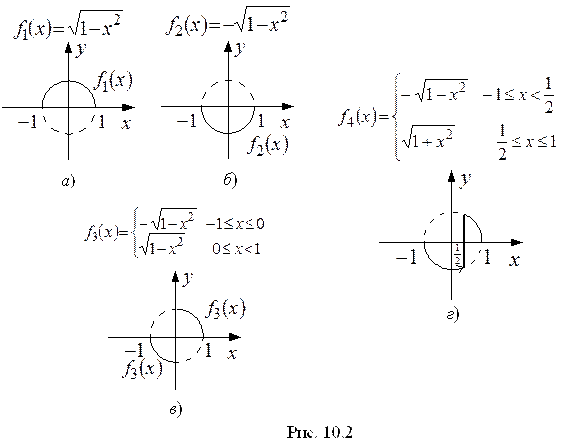 |
|
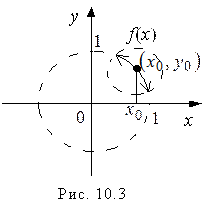
|
3) Уравнение 
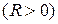 задает бесконечное множество неявных функций, определенных при
задает бесконечное множество неявных функций, определенных при  , т.е.
, т.е.  – круг радиусом
– круг радиусом  . В самом деле, формула
. В самом деле, формула 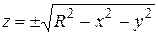 , в которой для каждой из точек
, в которой для каждой из точек  знак перед корнем выбирается произвольно, определяет неявную функцию. Заметим, что функции
знак перед корнем выбирается произвольно, определяет неявную функцию. Заметим, что функции  и
и  заданные в
заданные в  , непрерывны в
, непрерывны в  и дифференцируемы в
и дифференцируемы в 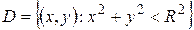 .
.
Следующие четыре теоремы даются для уравнения  .
.
Теорема 14 (существование неявной функции). Пусть функция  определена в цилиндре
определена в цилиндре  , непрерывна по
, непрерывна по  при фиксированных
при фиксированных  и
и  , и выполняется неравенство
, и выполняется неравенство  . Тогда существует, по крайней мере, одна неявная функция
. Тогда существует, по крайней мере, одна неявная функция  , заданная уравнением
, заданная уравнением
 , (38)
, (38)
определенная на множестве  .
.
‰ Пусть 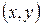 произвольная точка принадлежащая
произвольная точка принадлежащая  . По условию теоремы функции
. По условию теоремы функции  , при фиксированных значениях
, при фиксированных значениях  , непрерывна на
, непрерывна на  . В силу теоремы Коши (из свойств функций непрерывных на отрезке) функция
. В силу теоремы Коши (из свойств функций непрерывных на отрезке) функция 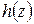 принимает любое промежуточное значение между
принимает любое промежуточное значение между  и
и  . Так как
. Так как  и
и  имеют различные знаки, то
имеют различные знаки, то 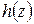 принимает и нулевое значение, т.е. существует хотя бы одна точка
принимает и нулевое значение, т.е. существует хотя бы одна точка  , в которой
, в которой  . Положим,
. Положим,  . Таким образом построена неявная функция
. Таким образом построена неявная функция  , определенная на
, определенная на  . <
. <
Теорема 15 (единственность). Пусть  определена в цилиндре
определена в цилиндре  , при фиксированных
, при фиксированных  и
и  из области
из области  и строго монотонна по переменной
и строго монотонна по переменной  . Тогда не может существовать более одной неявной функции
. Тогда не может существовать более одной неявной функции  , определенной на
, определенной на  .
.
‰ Предположим, что существуют две различные функции  и
и  , заданные уравнением (38). Тогда найдется такая хотя бы одна точка
, заданные уравнением (38). Тогда найдется такая хотя бы одна точка  , что
, что  . Однако из сделанного предположения, имеем
. Однако из сделанного предположения, имеем 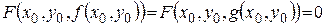 . Последнее невозможно, так как
. Последнее невозможно, так как  строго монотонна по
строго монотонна по  , т.е.
, т.е. 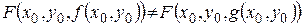 . Получаем противоречие с условием. Следовательно, функция
. Получаем противоречие с условием. Следовательно, функция  единственна. <
единственна. <
Следствие. Пусть функция  непрерывна по переменной
непрерывна по переменной  в цилиндре
в цилиндре  и
и 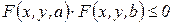 для точки
для точки  . Пусть также
. Пусть также  дифференцируема по
дифференцируема по  в открытом цилиндре
в открытом цилиндре  , причем
, причем  сохраняет знак в этом цилиндре. Тогда уравнение (38) задает единственную неявную функцию, определенную на множестве
сохраняет знак в этом цилиндре. Тогда уравнение (38) задает единственную неявную функцию, определенную на множестве  .
.
‰ По теореме 1 существует, по крайней мере, одна неявная функция  . Так как
. Так как  сохраняет знак в открытом цилиндре, то
сохраняет знак в открытом цилиндре, то  строго монотонна по
строго монотонна по  на
на  . Следовательно, по теореме 15 неявная функция
. Следовательно, по теореме 15 неявная функция  определена единственным образом. <
определена единственным образом. <
Теорема 16 (непрерывность неявной функции). Пусть функция  непрерывна в цилиндре
непрерывна в цилиндре  ; для любой точки
; для любой точки  выполняется условие
выполняется условие  ; функция
; функция  дифференцируема в открытом цилиндре
дифференцируема в открытом цилиндре  и
и  в
в  . Тогда уравнение (1) определяет единственным образом неявную функцию
. Тогда уравнение (1) определяет единственным образом неявную функцию  , которая непрерывна на множестве
, которая непрерывна на множестве  .
.
‰ Существование и единственность неявной функции  определяются следствием и теоремой 15. Для доказательства непрерывности функции
определяются следствием и теоремой 15. Для доказательства непрерывности функции  рассмотрим разность
рассмотрим разность  . Применяя формулу конечных приращений Лагранжа, получаем
. Применяя формулу конечных приращений Лагранжа, получаем
 (39)
(39)
Положим  , тогда
, тогда  . Следовательно,
. Следовательно,  . Используя условие
. Используя условие  , из (39) получаем
, из (39) получаем

 . (40)
. (40)
Переходя в неравенствах (40) к пределу при  в силу непрерывности функции
в силу непрерывности функции  , имеем
, имеем
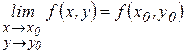 .
.
Следовательно, неявно заданная функция  непрерывна в любой точке
непрерывна в любой точке  .
.
<
Теорема 17 (дифференцирование неявной функции). Пусть функция  непрерывна в цилиндре
непрерывна в цилиндре  , где
, где  открытое множество; выполняется условие
открытое множество; выполняется условие  ; функция
; функция  дифференцируема в открытом цилиндре
дифференцируема в открытом цилиндре  и
и  . Тогда уравнение (38) определяет единственным образом неявную функцию
. Тогда уравнение (38) определяет единственным образом неявную функцию  , которая дифференцируема на
, которая дифференцируема на  и справедливы равенства
и справедливы равенства
 ,
,  , (41)
, (41)
где  .
.
‰ Существование и единственность неявной функции  вытекает из теорем 14 и 15. При этом
вытекает из теорем 14 и 15. При этом  непрерывна на
непрерывна на  по теореме 16. Так как функция трех переменных
по теореме 16. Так как функция трех переменных  дифференцируема на открытом множестве
дифференцируема на открытом множестве  , то
, то
 (42)
(42)
где  при
при  .
.
Положим  , тогда для точки
, тогда для точки 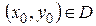 имеем
имеем  и
и
 ,
,  . (43)
. (43)
Из (42) и (43) получим
 .
.
Так как  , то
, то
 . (44)
. (44)
Поскольку  непрерывна, то
непрерывна, то  при
при  . Следовательно, так как
. Следовательно, так как  ,
,  и
и 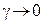 при
при  , то по теореме о пределе отношения двух функций получаем
, то по теореме о пределе отношения двух функций получаем
 ,
,  .
.
Отсюда следует, что

 , (45)
, (45)
где 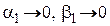 при
при  .
.
Из (44) и (45) следует
 .
.
Таким образом,  дифференцируемая функция в произвольной точке
дифференцируемая функция в произвольной точке  и
и
 ,
,  ,
,
где  . <
. <
Замечания.
1) Аналогичные теоремы имеют место для функционального уравнения
 . (46)
. (46)
Областью  здесь является интервал
здесь является интервал  , т.е.
, т.е. 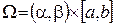 – прямоугольник на плоскости
– прямоугольник на плоскости 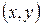 (рис. 8). Здесь неявная функция
(рис. 8). Здесь неявная функция  , а ее производные вычисляются по формуле
, а ее производные вычисляются по формуле
 . (47)
. (47)

|
2) Важным в теореме 17, а, следовательно, в формуле (41) и в формуле (47) является отличие от нуля производной стоящей в знаменателе. Например, если 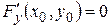 , то уравнение (46) может иметь не единственное решение относительно функции в точке
, то уравнение (46) может иметь не единственное решение относительно функции в точке  , а может не иметь ни одного, решения. Например, для уравнения
, а может не иметь ни одного, решения. Например, для уравнения  получаем
получаем  ,
,  , а
, а  . Очевидно, что в окрестности точки (1, 0) при
. Очевидно, что в окрестности точки (1, 0) при  , уравнение не имеет решения относительно
, уравнение не имеет решения относительно  , т.е. неявная функция не существует. А при
, т.е. неявная функция не существует. А при  , уравнение
, уравнение  имеет два решения
имеет два решения  и
и  , т.е. задает две неявные функции.
, т.е. задает две неявные функции.
Вместе с тем, надо отметить, что условия  (или
(или  ) являются лишь достаточными. Если они не выполняются, то неявная функция может существовать. Например, для уравнения
) являются лишь достаточными. Если они не выполняются, то неявная функция может существовать. Например, для уравнения  в точке (0, 0) они не выполняется, однако, в окрестности точки (0, 0) существует единичная неявная функция
в точке (0, 0) они не выполняется, однако, в окрестности точки (0, 0) существует единичная неявная функция  .
.
Пример. Доказать, что уравнение

определяет единственную неявную функцию  , и найти производные
, и найти производные  .
.
Решение. Обозначим  . Так как
. Так как 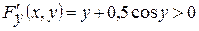 , то при любом фиксированном значении
, то при любом фиксированном значении  функция
функция  является возрастающей функцией переменной
является возрастающей функцией переменной  . Кроме того, для любого фиксированного значения
. Кроме того, для любого фиксированного значения  при достаточно больших значениях
при достаточно больших значениях  , очевидно, выполняются неравенства:
, очевидно, выполняются неравенства:  при
при  и
и  при
при  . Поскольку
. Поскольку  - непрерывная функция, то
- непрерывная функция, то  существует единственное
существует единственное  такое, что
такое, что 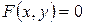 , следовательно,
, следовательно,  уравнение определяет единственную неявную функцию
уравнение определяет единственную неявную функцию  .
.
Теперь найдем производные. Так как  - дифференцируемая функция и
- дифференцируемая функция и  , то и функция
, то и функция  дифференцируема на всей числовой прямой. Для нахождения
дифференцируема на всей числовой прямой. Для нахождения 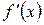 воспользуемся формулой (47):
воспользуемся формулой (47):
 =
= 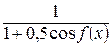 .
.
Дифференцируя  . Найдем
. Найдем
 .
.
Чтобы найти значения  в какой либо точке, нужно сначала вычислить соответствующее значение
в какой либо точке, нужно сначала вычислить соответствующее значение  в этой точке. Пусть
в этой точке. Пусть 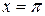 . Нетрудно проверить, что решением уравнения (49) при
. Нетрудно проверить, что решением уравнения (49) при 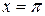 является
является 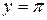 , т.е.
, т.е.  . Подставляя в полученные общие формулы, получаем
. Подставляя в полученные общие формулы, получаем  .
.
Неявные функции n переменных. Пусть задано уравнение
 (48)
(48)
или в векторном виде
 .
.
Функцию  будем предполагать заданной в цилиндре
будем предполагать заданной в цилиндре  :
:
 .
.
Если существует функция n переменных  , определенная на множестве
, определенная на множестве  , такая, что
, такая, что  , при
, при  , то говорят, что
, то говорят, что  неявная функция, заданная уравнением (48).
неявная функция, заданная уравнением (48).
Имеют место следующая теорема.
Теорема 18 (о неявной функции n переменных). Пусть выполняются следующие условия:
а)  ;
;
б)  дифференцируема в
дифференцируема в  ;
;
в) 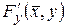 непрерывна в
непрерывна в  ;
;  .
.
Тогда найдутся  и
и  , что в некоторой окрестности точки
, что в некоторой окрестности точки 
 уравнение (48) имеет единственное решение
уравнение (48) имеет единственное решение  удовлетворяющее условию
удовлетворяющее условию  , причем
, причем  дифференцируемая и справедливы формулы:
дифференцируемая и справедливы формулы:
 . (49)
. (49)
Пример. Найти в точке  частные производные функции
частные производные функции  , заданной уравнением
, заданной уравнением  .
.
Решение. Из уравнения найдем значение функции  в данной точке
в данной точке  .
.
Функция  равна 0 в точке (1, 1, 2) и непрерывна в ее окрестности. Функции
равна 0 в точке (1, 1, 2) и непрерывна в ее окрестности. Функции

непрерывны, причем  . Следовательно, данное уравнение в окрестности точки (1, 1, 2)
. Следовательно, данное уравнение в окрестности точки (1, 1, 2)  определяет единственную непрерывно дифференцируемую функцию
определяет единственную непрерывно дифференцируемую функцию  , частные производные которой можно найти по формулам (48):
, частные производные которой можно найти по формулам (48):
 ,
,
 .
.
Теперь рассмотрим систему уравнений:

или в векторном виде:
 , (50)
, (50)
где  .
.
Пусть  – фиксированные точки.
– фиксированные точки.
Теорема 19 (о существовании решения системы неявных функций). Пусть выполняются условия:
а)  ;
;
б) функции  дифференцируемы в окрестности точки
дифференцируемы в окрестности точки  ;
;
в) частные производные  непрерывны в
непрерывны в  ;
;
г)  .
.
Тогда существуют  и
и  такие, что для
такие, что для  система уравнений
система уравнений 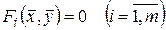 имеет единственное решение:
имеет единственное решение:
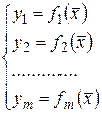 .
.
При этом 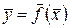 удовлетворяют условиям
удовлетворяют условиям  , и функции
, и функции  – дифференцируемы.
– дифференцируемы.
Векторные отображения
Пусть  точка множества
точка множества  и пусть на
и пусть на  заданы следующие функции n - переменных:
заданы следующие функции n - переменных:

Таким образом, для каждого фиксированного  можно рассматривать вектор
можно рассматривать вектор 
 . В этом случае говорят, что имеет место векторное отображение
. В этом случае говорят, что имеет место векторное отображение  или векторная функция
или векторная функция 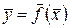 .
.
У векторной функции  , каждая координата
, каждая координата  является функцией n -переменных
является функцией n -переменных  . Функции
. Функции  называют координатными функциями отображения
называют координатными функциями отображения  , где
, где  записывают так
записывают так 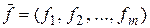 .
.
Если  , то пространства
, то пространства  и
и  можно считать совпадающими и функцию
можно считать совпадающими и функцию  можно интерпретировать как отображение
можно интерпретировать как отображение  в
в  . Такое отображение часто называют векторным полем,заданным на множестве
. Такое отображение часто называют векторным полем,заданным на множестве  . Важным классом векторных отображений
. Важным классом векторных отображений  являются линейные отображения или линейные векторные функции. Векторное отображение
являются линейные отображения или линейные векторные функции. Векторное отображение  называют линейным если
называют линейным если  и
и  , выполняется:
, выполняется:
 .
.
Из определения следует, что при линейном отображении любая линейная комбинация векторов  отображается в такую же линейную комбинацию образов этих векторов
отображается в такую же линейную комбинацию образов этих векторов
 .
.
Линейные отображения называют также линейными операторами.
В физических приложениях имеет место следующий частный случай векторных отображений. Пусть  , т.е.
, т.е. 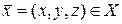 и
и 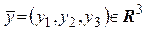 . Рассмотрим отображение
. Рассмотрим отображение  , т.е. векторное поле
, т.е. векторное поле
 ,
,
где  – три скалярных функции трех переменных или
– три скалярных функции трех переменных или  . Таким образом, каждой точке трехмерного геометрического пространства
. Таким образом, каждой точке трехмерного геометрического пространства  ставится в соответствие вектор этого же пространства. Примерами физических векторных полей являются:
ставится в соответствие вектор этого же пространства. Примерами физических векторных полей являются:
- поле гравитации;
- электрическое поле  ;
;
- магнитное поле 

- поле скорости жидкости  .
.
Пусть  и является предельной точкой множества
и является предельной точкой множества  , а
, а  . Отображение
. Отображение  задано функцией
задано функцией 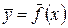 . Определим расстояние в пространстве
. Определим расстояние в пространстве  как
как
 .
.
Расстояние в пространстве  определяется следующим образом:
определяется следующим образом:

 .
.
Определение 25. Вектор  называют пределом отображения
называют пределом отображения  при
при  , если для любого положительного
, если для любого положительного  найдется такое неотрицательное число
найдется такое неотрицательное число  , что из выполнения условия
, что из выполнения условия  будет следовать выполнение неравенства
будет следовать выполнение неравенства  , т.е.
, т.е.  .
.
Предел отображения обозначается:
 .
.
Очевидно, что для любого 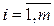 справедливы неравенства
справедливы неравенства
 .
.
Тогда ясно, что из условия (14) следует 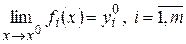 .
.
Определение 26. Пусть  и является его предельной точкой. Отображение
и является его предельной точкой. Отображение  называется непрерывным в точке
называется непрерывным в точке  , если оно определено в точке
, если оно определено в точке  и существует предел
и существует предел  при
при  равный
равный  , т.е.
, т.е.  .
.
Если  – изолированная точка множества
– изолированная точка множества  , то
, то  считается непрерывной в точке
считается непрерывной в точке  .
.
Ясно, что отображение  непрерывно в точке
непрерывно в точке  каждая функция
каждая функция  непрерывна в точке
непрерывна в точке  как функция n -переменных.
как функция n -переменных.
Определение 27. Отображение 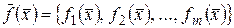 , определенное на открытом множестве
, определенное на открытом множестве  называется дифференцируемым в точке
называется дифференцируемым в точке  , если каждая функция
, если каждая функция  дифференцируема в точке
дифференцируема в точке  .
.
Так как каждая функция n - переменных 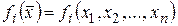 дифференцируемая в точке
дифференцируемая в точке  , то ее полное приращение в этой точке имеет вид
, то ее полное приращение в этой точке имеет вид
 ,
,
где  ;
;  .
.
Эти полные приращения  представляют собой m скалярных равенств, и их можно записать в векторном виде в пространстве
представляют собой m скалярных равенств, и их можно записать в векторном виде в пространстве 
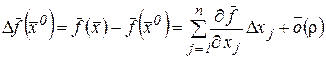 , (51)
, (51)
где
 , (52)
, (52)
 .
.
Более подробно (51) можно записать так:
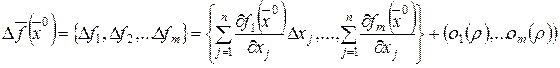 .
.
Определение 28. Векторы (52) называют частными производными отображения  в точке
в точке  по переменным
по переменным  .
.
Определение 29. Выражение  , линейное относительно переменных
, линейное относительно переменных  называют дифференциалом отображения
называют дифференциалом отображения  в точке
в точке  и обозначают
и обозначают
 . (53)
. (53)
Заметим, что  – дифференциал независимой переменной
– дифференциал независимой переменной  . Формулы (51) и (53) можно записать в матричной форме:
. Формулы (51) и (53) можно записать в матричной форме:
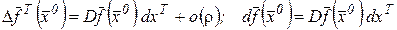 , (54)
, (54)
где матрица 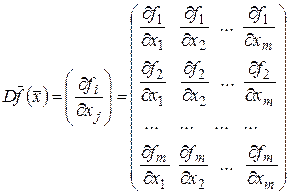
называется матрицей Якоби, а соответствующие векторы - столбцы имеют вид:
 ;
; 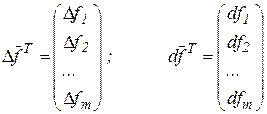 .
.
Матрица Якоби называется также производной вектор-функции  в точке
в точке  , и обозначается одним из способов:
, и обозначается одним из способов:
 .
.
Заметим, что градиент функции переменных  есть частный случай матрицы Якоби при
есть частный случай матрицы Якоби при  , и поэтому его также являют производной этой функции.
, и поэтому его также являют производной этой функции.
Определение 30. Отображение 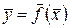 называется непрерывно дифференцируемым на открытом множестве
называется непрерывно дифференцируемым на открытом множестве  , если частные производные
, если частные производные  – непрерывны на множестве
– непрерывны на множестве  .
.
Если  , то матрица Якоби квадратная размерностью n:
, то матрица Якоби квадратная размерностью n:
 .
.
Определитель такой матрицы Якоби называется якобианом и обозначается
 .
.
Примеры. 1) Найти дифференциал отображения  в точке
в точке  , где
, где  .
.
Решение. Для функций  ,
, 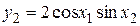 ,
,  найдем матрицу Якоби
найдем матрицу Якоби

в точке  . Получаем
. Получаем
 .
.
Тогда
 .
.
2) Найти якобиан  отображения
отображения 
Решение.
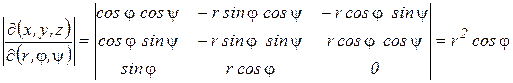 .
.
Снова рассмотрим случай, когда  . Здесь
. Здесь  – вектор-функция определенная на открытом множестве
– вектор-функция определенная на открытом множестве  . Будем интерпретировать
. Будем интерпретировать  как векторное поле на
как векторное поле на  .
.
Определение 31. Векторное поле  называется потенциальным на множестве X, если существует такая дифференцируемая функция n -переменных
называется потенциальным на множестве X, если существует такая дифференцируемая функция n -переменных  , что выполняются условия:
, что выполняются условия:
 .
.
Функция  называется потенциалом векторного поля
называется потенциалом векторного поля  . В силу дифференцируемости функции
. В силу дифференцируемости функции  следует:
следует:
 ,
,
или
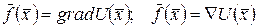 .
.
Таким образом, потенциал векторного поля есть функция  , градиентом некоторой является функции
, градиентом некоторой является функции  , т.е. само векторное поле.
, т.е. само векторное поле.
Из определения следует, что потенциал векторного поля  определяется с точностью до постоянного числа С. Если
определяется с точностью до постоянного числа С. Если  и
и  два потенциала векторного поля
два потенциала векторного поля  , то
, то  .
.
Теорема 20. Для того чтобы дифференцируемое векторное поле, определенное в  , было потенциальным, необходимо выполнение следующих условий:
, было потенциальным, необходимо выполнение следующих условий:
 .
.
‰ Пусть  – потенциал поля
– потенциал поля  , тогда
, тогда  . Из дифференцируемости векторного поля
. Из дифференцируемости векторного поля  следует, что
следует, что  дважды дифференцируема на
дважды дифференцируема на  . Тогда в силу теоремы о равенстве смешанных производных
. Тогда в силу теоремы о равенстве смешанных производных
 . ■
. ■
Замечание. Для векторного поля на плоскости 
 и необходимое условие имеет вид:
и необходимое условие имеет вид:
 .
.
Для векторного поля в прост