, 
, 
Уравнения движения есть также уравнения траектории точки в параметрической форме. Параметром является время t.
2) Скорость точки при векторном способе задания движения. Средней скоростью 
называется отношение изменения радиус-вектора 
к изменению времени 
.
Скорость точки равна первой производной по времени от ее радиус-вектора
Скорость точки равна первой производной по времени от ее радиус-вектора. Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.
3) Центростремительное или Нормальное ускорение 
— возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда 
итд). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен: 
Тангенциальное ускорение — 
направлено по касательной к траектории (обозначается иногда и т.д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
4) Поступательным движением твёрдого тела называется такое его движение, при котором любая прямая, жёстко скреплённая с телом, остаётся параллельной своему первоначальному положению в каждый момент времени
Теорема. При поступательном движении твёрдого тела траектории, скорости и ускорения всех точек твердого тела одинаковы
Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения.
5) 5).Передаточное число (
) находится как отношение числа зубьев колеса (
) к числу зубьев шестерни (
) в зубчатой передаче, числа зубьев червячного колеса к числу заходов червяка в червячной передаче, числа зубьев большой звёздочки к числу зубьев малой в цепной передаче, а также диаметра большого шкива (или катка) к диаметру меньшего в ремённой или фрикционной передаче. Передаточное число используется при расчётах геометрических параметров зубчатых передач.[1] [2]
6) 6).сложного движения — когда материальная точкадвижется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета
7) 7).Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Теорема. Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое — относительное.
В частности, движение плоской фигуры в ее плоскости относительно системы, расположенной в той же плоскости, можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат, начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат вращением вокруг подвижной оси, перпендикулярной плоской фигуре и проходящей через выбранный полюс.
Для доказательства этого достаточно показать, что плоскую фигуру в ее плоскости из одного положения в любое другое можно перевести двумя перемещениями — поступательным перемещением в плоскости фигуры вместе с каким —либо полюсом и поворотом в той же плоскости вокруг этого полюса.
9)Мгнове́нный центр скоросте́й — при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.
Поскольку при движении плоской фигуры в каждый момент времени существует точка (МЦС), жестко связанная с плоской фигурой, скорость которой в этот момент равна нулю, то при определении скоростей эту точку и следует выбирать в качестве полюса, играющего роль центра вращения в данный момент времени.
10)) если известны направления скоростей 
и 
точек А и В плоской фигуры, то МЦС (точку Р) определяют как точку пересечения перпендикуляров к скоростям и , проведенных из этих точек (рис. 3.3,а);
2) если скорости двух точек тела A и B известны по модулю, параллельны друг другу ( || ), и перпендикулярны прямой AB, то МЦС находят в точке пересечения прямой АВ с прямой, соединяющей концы векторов скоростей и (рис. 3.3,б,в);
3) при качении без скольжения одного тела по неподвижной поверхности МЦС находят в точке соприкосновения тел (рис. 3.3,г), так как при отсутствии скольжения скорость этой точки подвижного тела равна нулю;
4) если скорости точек A и B тела и параллельны друг другу ( || ) и не перпендикулярны прямой АВ, то перпендикуляры к ним также параллельны друг другу. В этом случае МЦС находится в бесконечном удалении от точек A и B, движение тела является мгновенно поступательным, следовательно, скорости всех точек тела равны, а его угловая скорость в данный момент времени равна нулю.
С помощью МЦС плоскопараллельное движение можно представить не только как сложное, состоящее из поступательного и вращательного движений, но и как простое движение, состоящее из серии элементарных последовательных поворотов вокруг МЦС. Необходимо отметить, что положение МЦС в пространстве во все время движения меняется. Геометрическое место точек МЦС подвижного тела называют подвижной центроидой, а неподвижного тела – неподвижной центроидой. Таким образом, плоскопараллельное движение представляет собой качение без скольжения подвижной центроиды по неподвижной центроиде.
11) Ускорение любой точки тела при плоском движении равно геометрической сумме ускорения полюса и ускорения во вращении точки относительно полюса.
Следствие 1. Проекции скоростей точек тела при его плоском движении на прямую, соединяющую точки, равны.
Следствие 2. Разность проекций скоростей точек прямолинейного отрезка АВ на перпендикуляр к АВ равна скорости во вращении одной точки относительно другой.
Следствие 3. Концы векторов скоростей точек прямолинейного отрезка лежат на одной прямой и делят отрезок между концами векторов скоростей крайних точек на части в том же отношении, в каком точки делят сам отрезок.
Следствие 4. В любой момент непоступательного движения плоской фигуры на плоскости, связанной с фигурой, существует точка, скорость которой равна нулю.
12) Мгнове́нный центр ускоре́ний — при непоступательном движении точка, находящаяся в плоскости движения тела, ускорение которой в данный момент времени равно нулю. Для того, чтобы определить положение мгновенного центра ускорений, необходимо к векторам ускорений двух различных точек тела провести прямые под равными углами μ. В точке пересечения проведённых прямых и будет находиться мгновенный центр ускорений. Угол μ должен удовлетворять равенству:
13) Кориолиса ускорение, поворотное ускорение, часть полного ускорения точки, появляющаяся при т. н. сложном движении когда переносное движение, т. е. движение подвижной системы отсчёта, не является поступательным. Кориолиса ускорение появляется вследствие изменения относительной скорости точки uотнпри переносном движении (движении подвижной системы отсчёта) и переносной скорости при относительном движении точки. Численно Кориолиса ускорение
vkop=2wпер uотн sin a,
14) Динамикой наз-ся раздем механики,в котором изучается движение материальных тел под действием сил.
1. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
2. Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точкесилой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
3. Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
15) Свободной называют точку, на которую не наложены связи. В противном случае точка является несвободной и тогда, согласно принципу освобождаемости от связей к точке прикладывают реакции отброшенных связей, кроме активных сил.
Если на свободную точку действует система активных сил, равнодействующая которой 
, то согласно 2-му закону Ньютона следует, что
.
Полученное выражение называют основным уравнением динамикисвободной материальной точки в векторной форме.
Если движение точки задано в векторной форме 
, то, как известно из раздела кинематики,
и формулу (1.1) можно записать следующим образом
.
Нужно отметить, что в общем случае сила 
может быть функцией времени, положения и скорости точки
.
Равенство (1.3) представляет собой векторное дифференциальное уравнение движения свободной материальной точки. В проекциях на оси инерциальной декартовой системы координат оно примет вид:
.
При движении точки в плоскости xOy, так как 
, систему уравнений можно записать так:
.
Если точка движется прямолинейно вдоль какой-либо оси, например Ox, так как 
, получим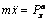 
.
В проекциях на оси (касательную, нормаль и бинормаль к траектории точки) естественной системы координат равенство (1.3) запишем следующим образом
.
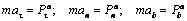Из кинематики известно, что
.
Поэтому рассматриваемые выражения примут вид:
,
где 
– уравнение движения точки по соответствующей траектории; ρ – радиус кривизны траектории; 
– проекции равнодействующей сил, приложенных к точке на оси естественной системы координат.
Если точка несвободна то на нее, кроме равнодействующей активных сил , будет действовать равнодействующая реакций связей 
. Тогда уравнение (1.1) запишем так:
.
Полученное выражение называют основным уравнением динамики несвободной материальной точки в векторной форме. Оно принимает такой вид:
– в проекциях на оси декартовой системы координат
;
– в проекциях на оси естественной системы координат
или
.
1. Первой или прямой называется задача, в которой заданы масса точки и закон ее движения в декартовых координатах или в естественной форме.
2. Второй или обратной называется задача, в которой по заданным силам и массе материальной точки определяется ее движение.
18). Система материальных точек или механическая система – Совокупность материальных точек или материальных тех, объединяемых общими законами взаимодействия (положение или движение каждой из точек или тела зависит от положения и движения всех остальных) Система свободных точек - движение которых не ограничивается никакими связями (например, планетная система, в которой планеты рассматриваются как материальные точки). Система несвободных точек или несвободная механическая система – движение материальных точек или тел ограничиваются наложенными на систему связями (например, механизм, машина и т.п .). Силы, действующие на систему. В дополнение к ранее существовавшей классификации сил (активные и реактивные силы) вводится новая классификация сил: 1. Внешние силы (e) – действующие на точки и тела системы со стороны точек или тел, не входящих в состав данной системы. 2. Внутренние силы (i) – силы взаимодействия между материальными точками или телами, входящими в данную систему. Одна и та же сила может являться как внешней, так и внутренней силой. Все зависит от того, какая механическая система рассматривается. Внутренние силы Fi – силы, вызванные взаимодействием точек, входящих в систему. Свойства внутренних сил: 1) Геометрическая сумма (главный вектор) всех внутренних сил = 0; 2) Геометрическая сумма моментов всех внутренних сил относительно произвольной точки = 0.
19) Центр масс — воображаемая точка С, положение которой характеризует распределение масс этой системы.
Закон движения центра масс — в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
; 
; 
Система центра масс — система отсчёта, относительно которой центр масс механической системы неподвижен. Следствие 1. Если главный вектор внешних сил, приложенных к механической системе, равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно. Так как ускорение центра масс равно нулю,.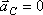 
Следствие 2. Если проекция главного вектора внешних сил на какую-нибудь ось равна нулю, то центр масс системы или не изменяет своего положения относительно данной оси, или движется относительно нее равномерно.
21) Количество движения механической системы равно произведению массы системы на скорость ее центра инерции.
Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количеств движения всех материальных точек этой системы.
Теорема: Для системы: производная от количества движения системы по времени равна главному вектору внешних сил системы (векторной сумме внешних сил, приложенных к системе):
или в координатной форме: 
22) Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
В случае непрерывного распределения масс эта сумма сводится к интегралу
Формулы:
23) Момент инерции тела зависит от выбора оси, относительно которой он определяется. Теорема Гюйгенса-Штейнера позволяет ограничиться вычислением моментов инерции тел, проходящих лишь через его центр инерции. Она гласит:
Момент инерции тела 
относительно какой-либо оси 
равен моменту инерции его относительно параллельной оси, 
проходящей через центр масс (
), сложенному с произведением массы тела на квадрат расстояния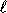 
между параллельными осями:
Теорема Гюйгецса-Штейнера.Эта теорема связывает моменты инерции относительно двух параллельных осей, одна из которых проходит через центр масс тела.
Ось 1 на рис. 2.18 проходит через центр масс О, ось 2 параллельна ей; расстояние между осями равно 
и 
- векторы, перпендикулярные осям 1 и 2. Они проведены от осей в ту точку, где расположена масса 
Момент инерции тела относительно оси 2
Последняя сумма равна нулю, поскольку ось 1 проходит через центр масс, и
Если, например, ось - касательная к поверхности шара, то можно, не проводя громоздких вычисление, записать: 
24) Теорема об изменении момента количества движения матер. точки. - момент количества движения матер. точки относительно центра О. – производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения: и т.д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, МО= 0, Þ =const. =const, где – секторная скорость. Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки описывает ("ометает") равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера.
25) Момент количества движения (или кинетический момент) механической системы относительно центра О или оси z равен соответственно геометрической или алгебраической сумме Момент количества движ, т. е. Ko = Skoi, Kz = Skzi. Вектор Ko может быть определён его проекциями Kx, Ky, Kz на координатные оси. Для тела, вращающегося вокруг неподвижной оси z с угловой скоростью w, Kx = — Ixzw, Ky = —Iyzw, Kz = Izw, где lz — осевой, а Ixz, lyz — центробежные моменты инерции. Если ось z является главной осью инерции для начала координат О, то Ko = Izw.ения всех точек системы относительно того же центра или оси.
30) Принцип Даламбера (метод кинетостатики)
В каждый момент движения сумма активных сил, реакций связей и сил инерции равна нулю 
— принцип Даламбера для материальной точки.
– внешняя сила, 
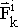– внутренняя сила. Сила инерции: 
, знак (–) показывает, что сила инерции направлена в противоположную сторону ускорению.
Для системы добавляется уравнение моментов:. 
Обозначают: 
– главный вектор сил инерции, 
– главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и сумма их моментов равна нулю, 
, 
получаем: 
, 
— уравнения кинетостатики. Принцип Даламбера для системы – если в любой момент времени к каждой точке системы приложить, кроме реально действующих сил, соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно применять уравнения статики. Это упрощает процесс решения задач.
Главный вектор сил инерции 
равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.
Главный момент сил инерции зависит от вида движения: при поступательном движении 
; при плоском 
, при вращении вокруг оси z, проходящей через центр масс тела, 
.
32) ОБОБЩЁННЫЕ КООРДИНАТЫ
независимые параметры qi (i=1, 2,..., s) любой размерности, число к-рых равно числу s степеней свободы механич. системы и к-рые однозначно определяют положение системы. Закон движения системы в О. к. даётся s ур-ниями вида qi=qi(t), где t — время. О. к. пользуются при решении мн. задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число ур-ний, описывающих движение системы, по сравнению, напр., с ур-ниями в декартовых координатах (см. ЛАГРАНЖА УРАВНЕНИЯ В МЕХАНИКЕ). В системах с бесконечно большим числом степеней свободы (сплошные среды, физ. поля) О. к. являются особые функции пространственных координат и времени, наз. потенциалами, волн. функциями и т. п.
ОБОБЩЁННЫЕ СИЛЫ
величины, играющие роль обычных сил, когда при изучении равновесия или движения механич. системы её положение определяется обобщёнными координатами. Число О. с. равно числу s степеней свободы системы; при этом каждой обобщённой координате qi соответствует своя О. с. Qi. Значение О. с. Q1, соответствующей координате q1, можно найти, вычислив элем. работу dA1 всех сил на возможном перемещении системы, при к-ром изменяется только координата q1:, получая приращение dq1. Тогда dA1=Q1dq1т. е. коэффициент при dqi в выражении dA1 и будет О. с. Q1. Аналогично вычисляются Q2, Q3,..., Qs.
Размерность О. с. зависит от размерности обобщённой координаты. Если qi имеет размерность длины, то Qi — размерность обычной силы; если qi — угол, то Qi имеет размерность момента силы, и т. д. При изучении движения механич. системы О. с, входят вместо обычных сил в Лагранжа уравнения механики, а при равновесии все О. с. равны нулю.