Метод поиска по симплексу

Численные методы многомерной оптимизации

 

Методы нулевого порядка.

 

3.1. Метод Хука-Дживса (метод конфигураций).

Требуется найти безусловный минимум функции, то есть найти такую точку , что .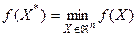

Стратегия поиска.

Метод использует информацию, полученную на текущем шаге для определения направления поиска на последующем шаге. Реализуется в два этапа [3-5].

I этап — исследующий поиск. На этом этапе осуществляется выбор перспективного направления уменьшения функции. Точка, из которой на k -ой итерации осуществляется поиск перспективного направления называется базовой: .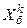

Задается величина шага , j =1, n, которая может быть различной для разных координатных направлений. Вычисляются значения функции и , и по каждой из переменных определяется направление уменьшения функции. В результате исследующего поиска определяют точку X^{k ,} которая вместе с точкой 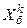задет прямую — направление поиска (рисунок 3).

II этап – поиск по образцу. На этом этапе осуществляется движение вдоль выбранного направления в соответствии с выражением

, (3.1)

где λ представляет собой ускоряющий множитель, при λ =1 выражение (3.1) примет вид . Движение вдоль прямой осуществляется до тех пор, пока выполняется условие (2.2). Если в точке X^{k +1} получено значение функции большее, чем в предыдущей точке X^k, движение вдоль выбранного направления прекращают и точку объявляют текущей базовой ткой. Одна итерация завершается. Далее этапы поиска повторяются.

В ситуации, когда исследующий поиск по всем координатам не приводит к результату, изменяют длину шага, уменьшая в несколько раз, например, 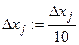. Графическая интерпретация метода Хука-Дживса представлена на рисунке 3.

 

 

Рисунок 3 — Приближение к минимуму функции на основе алгоритма Хука-Дживса

 

Алгоритм

Шаг 1. Задать начальную точку X ⁰; число для завершения алгоритма; начальные величины шагов по координатным направлениям , i= 1 ,n; ускоряющий множитель α >0; коэффициент уменьшения шага λ >1. Положить Y ¹= X ⁰, i =1, k =0.

Введем вектор-столбец направления d_i. Все компоненты вектора равны нулю, кроме i-й компоненты.

Шаг 2. Осуществить исследующий поиск по выбранному координатному направлению:

а) если , то есть

, шаг считается удачным. В этом случае положить и перейти к шагу 3;

б) если в п. «а» шаг неудачен, то делается шаг в противоположном направлении. Если , то и перейти к шагу 3.

в) если шаги в п. «а» и «б» неудачны, то .

Шаг 3. Проверить условия:

а) если i < n, то положить i = i +1 и перейти к шагу 2 (продолжить исследующий поиск по направлениям);

б) если i = n, проверить успешность исследующего поиска:

- если ,перейти к шагу 4;

- если , перейти к шагу 5.

Шаг 4. Провести поиск по образцу. Положить

Двигаться вдоль выбранного направления

, l = l +1,

пока значения функции будут уменьшаться f (Z^{l +2})< f (Z^{l +1}).

Как только неравенство нарушится, положить k = k +1, i =1, 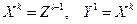и перейти к шагу 2.

Шаг 5. Проверить условие окончания:

а) если все поиск закончить и считать ;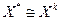

б) для тех i, для которых , уменьшить величину шага Положить Y ¹= X^k, X^{k +1}= X^k, k = k +1, i =1 и перейти к шагу 2.

Пример 3. Выполнить приближение к локальному минимуму функции f (X)=2 x ₁²+ x ₁ x ₂+ x ₂² на основе двух итераций в соответствии с методом Хука-Дживса.

1 ⁰. Начальная точка поиска X ⁰=(0,5;1) ^Т; число для завершения алгоритма; начальные величины шагов по координатным направлениям 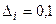, i= 1, 2; ускоряющий множитель α =1; коэффициент уменьшения шага λ =0,1. Положить Y ¹= X ⁰=(0,5;1) ^Т, i =1, k =0. При этом значение функции в базовой точке равно f (Y ¹)= f (X ⁰)= f (0,5;1) ^Т =2.

2 ⁰¹. Осуществить исследующий поиск по выбранному координатному направлению x_i, i =1:

f (0,5+0,1;1)= f (0,6; 1)=2,32 — шаг неудачен;

f (0,5-0,1;1)= f (0,4; 1)=1,72 — лучшее направление для переменной x ₁, Y ²=(0,4; 1).

3 ⁰¹. Проверить условие: i <2, i = i +1=2, перейти к шагу 2 и продолжить поиск по координатным направлениям.

2 ⁰². Осуществить исследующий поиск по выбранному координатному направлению x_i, i =2:

f (0,4; 1+0,1)= f (0,4; 1,1)=1,97 — шаг неудачен;

f (0,4; 1-0,1)= f (0,4; 0,9)=1,49 — лучшее направление для переменной x ₂.

3 ⁰². Проверить условие: i =2, проверить успешность исследующего поиска: f (Y^{n+ 1})= f (Y ³)=1,49< f (X ⁰)= f (0,5;1)=2, Y ³=(0,5;1), перейти к шагу 4.

4 ¹. Выполнить поиск по образцу, положить l =0, , тогда 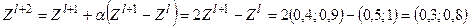f (Z^{l +2})= f (Z ²)=1,06< f (Z^{l +1})= f (Z ¹)=1,49, l = l +1=1. Поскольку поиск по образцу успешен, двигаемся дальше вдоль выбранного направления, увеличивая l.

f (Z ³)= f (0,2; 0,7)=0,71 < f (Z ¹)=1,06, l = l +1=2.

f (Z ⁴)= f (0,1; 0,6)=0,44 < f (Z ²)=0,71, l = l +1=3.

f (Z ⁵)= f (0,0; 0,5)=0,25 < f (Z ³)=0,44, l = l +1=4.

f (Z ⁶)= f (-0,1; 0,4)=0,14 < f (Z ⁴)=0,25, l = l +1=5.

f (Z ⁷)= f (-0,2; 0,3)=0,11 < f (Z ⁵)=0,14, l = l +1=6.

f (Z ⁸)= f (-0,3; 0,2)=0,16 > f (Z ²)=0,14, поиск по образцу прекращается, k = k +1=1, i =1, 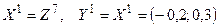и перейти к шагу 2.

2 ¹¹. Осуществить исследующий поиск по выбранному координатному направлению x_i, i =1:

f (-0,2+0,1;0,3)= f (-0,1; 0,3)=0,08 — шаг удачный, Y ²=(-0,1; 0,3).

3 ¹¹. Проверить условие: i <2, i = i +1=2, перейти к шагу 2.

2 ¹². Осуществить исследующий поиск по выбранному координатному направлению x_i, i =2:

f (-0,1; 0,3+0,1)= f (-0,1; 0,4)=0,14 — шаг неудачен;

f (-0,1; 0,3-0,1)= f (-0,1; 0,2)=0,04— лучшее направление для переменной x ₂.

3 ¹². Проверить условие: i =2, проверить успешность исследующего поиска: f (Y ³)=0,04< f (X ¹)= f (-0,2;0,3)=0,11, Y ³=(-0,1; 0,2), перейти к шагу 4.

4 ¹. Выполнить поиск по образцу, положить l =0, 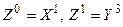, тогда

f (Z^{l +2})= f (Z ²)=0,01 < f (Z^{l +1})= f (Z ¹)=0,04, l = l +1=1. Поскольку поиск по образцу успешен, двигаемся дальше вдоль выбранного направления, увеличивая l.

f (Z ³)= f (0,1; 0)=0,02 > f (Z ¹)=0,01, поиск по образцу прекращается, k = k +1=2, i =1, и перейти к шагу 2.

На следующей итерации исследующий поиск может не привести к успеху. В такой ситуации необходимо уменьшить величину шага по координатным направлениям и продолжить вычисления согласно алгоритму.

В результате выполнения двух итераций получили следующий результат: X ^*= X ²=(0; 0,1), f (X ^*)=0,01.

 

 

Метод поиска по симплексу

Требуется найти безусловный минимум функции, то есть найти такую точку , что .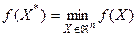

Стратегия метода.

В основу метода поиска по симплексу положено построение последовательности систем n +1 точек Xⁱ (k), i =1,… n +1, которые являются вершинами регулярного симплекса, то есть выпуклого многогранника, образованного n +1 вершиной [4,5]. Например, если n =2, то регулярный симплекс представляет собой равносторонний треугольник. Точки системы Xⁱ (k +1), i =1,… n +1 совпадают с точками системы Xⁱ (k), i =1,… n +1, кроме i=j, где точка X^j (k) — наихудшая в системе Xⁱ (k), i =1,… n +1, то есть 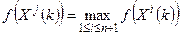. Точка X^j (k) заменяется на другую по следующим правилам. Худшая, с точки зрения значений функции вершина, отражается относительно центра тяжести X^C (k) остальных точек симплекса (рисунок 4а). Системе точек k принадлежат точки X ¹, X ² и X ³. Если точка X ¹ является наихудшей в системе k, то она отражается через центр тяжести вершин X ² и X ³. Строится k +1-я система точек. В нее входят точки X ² и X ³ и новая точка X ⁴, построенная в результате отражения точки X ¹ (рисунок 4б).

а) б)

Рисунок 4 — Отражение точек в регулярном симплексе: а) положение центра тяжести; б) построение отраженной точки.

 

Построение регулярных симплексов завершается, когда разность между минимальными значениями функции в системах k и k +1 достаточно малы, то есть

, i =1,… n +1. (3.2)

Реализация алгоритма основана на вычислениях двух типов: построении регулярного симплекса при заданных базовой точке и масштабном множителе и расчете координат отраженной точки.

1. Построение симплекса. Пусть X⁰ – начальная (базовая) точка поиска; α – масштабный множитель, определяющий размер симплекса. Координаты остальных n вершин определяются по формуле:

, (3.3)

где . (3.4)

Верхний индекс – номер вершины, нижний – номер компоненты в векторе X.

2. Отражение вершины относительно центра тяжести. Пусть X^j – вершина, подлежащая отражению. Центр тяжести остальных n вершин расположен в точке

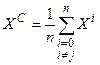(3.5)

Все точки прямой, проходящей через X^j и X^C задаются выражением

. (3.6)

Регулярный симплекс можно построить, если выбрать λ =2,тогда выражение (3.6) примет вид

,

где — точка k +1-го симплекса, 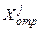— точка k -го симплекса, подлежащая отражению.

Рисунок 5 — Приближение к точке минимума функции на основе метода поиска по симплексу.

Замечания

1. Если вершина, которой соответствует наибольшее значение целевой функции построена на предыдущей итерации, то вместо нее берется вершина, которой соответствует следующее по величине значение функции.

2. Если некоторая вершина симплекса повторяется на протяжении более, чем М итераций, то необходимо уменьшить размеры симплекса и построить новый, выбрав в качестве базовой точку ту, которой соответствует минимальное значение целевой функции. Предложено принимать M =1,65 N +0,5 N ², где N – размерность задачи, а М необходимо округлить до ближайшего целого.

 

 

Алгоритм

Шаг 1. Задаются параметры задачи: базовая точка X⁰, масштабный множитель α, точность вычислений ε, предельное число итераций M, коэффициент уменьшения симплекса γ >1. Положить k =0. Определить первоначальный симплекс в соответствии с (3.3) и (3.4).

Шаг 2. Среди вершин симплекса выбирается та, в которой функция принимает наибольшее значение. .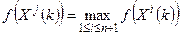

Шаг 3. Строится новый симплекс в соответствии с (3.5) и (3.6)..

Шаг 4. Проверяются условия замечаний 1 и 2. Если вершина симплекса не принадлежала ранее построенным симплексам, то k = k +1 и перейти к шагу 2;

иначе перейти к шагу 5.

Шаг 5. Проверяется условия завершения:

- замечание 3 выполнено, ;

- иначе – перейти к шагу 2.

 

Пример 3. Выполнить приближение к локальному минимуму функции f (X)=2 x ₁²+ x ₁ x ₂+ x ₂² на основе двух итераций в соответствии с методом поиска по симплексу.

1 ⁰. Начальная точка поиска X ⁰(0)=(0,5;1) ^Т; масштабный множитель α= 0,5. Положить k =0. Определим первоначальный симплекс в соответствии с (10) и (11) и вычислим значения функции в вершинах k -го симплекса:

;

 

 

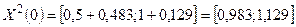
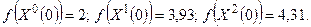
2 ⁰. Среди вершин симплекса выбирается та, в которой функция принимает наибольшее значение. Это вершина с координатами .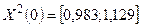

Значение функции в этой вершине симплекса: Она подлежит отражению.

3 ⁰. Для отражения вершины вычисляем координату центра тяжести остальных вершин симплекса в соответствии с (13):

.

Вычисляем координаты отраженной вершины:

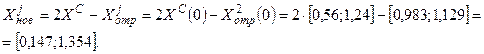4 ⁰. Вновь построенная вершина не принадлежит ранее построенным симплексам; k = k +1=1. Новый симплекс представляется следующими вершинами:

;

;

;

2 ¹. Среди вершин симплекса выбирается та, в которой функция принимает наибольшее значение. Это вершина с координатами .

Значение функции в этой вершине симплекса: Она подлежит отражению.

3 ¹. Для отражения вершины вычисляем координату центра тяжести остальных вершин симплекса в соответствии с (13):

.

Вычисляем координаты отраженной вершины:

4 ¹. Вновь построенная вершина не принадлежит ранее построенным симплексам; k = k +1=1. Новый симплекс представляется следующими вершинами:

;

;

;

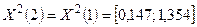На этом две итерации завершены. В новой точке, полученной на второй итерации, значение функции уменьшилось по сравнению с начальным значением.

 

4. методы первого порядка (градиентные методы).

 

Методы первого порядка, позволяющие решать задачу безусловной минимизации функций нескольких переменных основаны на использовании свойств производной функции:

- первая производная функции обращается в нуль в стационарных точках;

- направление поиска выбирается в соответствии с градиентом.

Предполагается, что функция f (X) и ее первая производная существуют и непрерывны. Компоненты градиента должны быть представлены в аналитической форме или вычислены с достаточной точностью на основе численных методов.

Все градиентные методы основаны на итерационной процедуре, реализуемой в соответствии с соотношением:

, (4.1)

где X^k — текущее приближение к решению X ^*; S (X^k)= S^k — направление поиска в n -мерном пространстве переменных x_i, i =1, …, n; α^k – длина шага вдоль выбранного направления.

Способы определения направления поиска S^k и длины шага вдоль этого направления α^k связаны с особенностями реализации того или иного метода.