Понятия функции двух переменных.

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

Лекция 1

Понятия функции двух переменных.

В большинстве случаев соотношения, с которыми приходится сталкиваться в экономике и бизнесе, связывают не две, как это предполагалось до сих пор, а сразу несколько величин. Например, ранее мы считали, что спрос на какой-либо товар определяется только одним фактором — ценой. В действительности это верно только частично.

На спрос могут также влиять: доходы потребителя Y, цена взаимозаменяемых 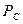и взаимодополняющих товаров, расходы на рекламу А, вкусы потребителя Т.

Взаимозаменяемыми товарами и услугами называются те, которые служат одним и тем же целям, когда покупателю безразлично, какие из товаров и услуг выбрать. Примерами могут служить автобусы и троллейбусы, куры и индейки и т.д. Взаимозаменяемость почти никогда не бывает абсолютной. Здесь важна связь между ценой на один товар и спросом на другой, взаимозаменяемый; если снизится цена на один товар, спрос на другой уменьшится, и наоборот,

Взаимодополняющими товарами называются те, которые в совокупности удовлетворяют одну и ту же потребность. Например, видеомагнитофоны и кассеты, автомобили и покрышки и т.д. Снижение цен на первые названные в паре товары приводит к расширению их продажи, что повышает спрос на дополняющие их товары.

Зависимость спроса от всех перечисленных выше факторов можно изобразить графически.

Если каждой упорядоченной паре (х, у) чисел из некоторого множества М по определенному правилу ставится в соответствие единственное число z, принадлежащее множеству N, то говорят, что задана функция двух переменных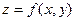

При этом множество M называется областью определения, а N — множеством значений функции.

Чтобы получить значения функции 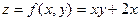нужно вместо х и у поставить данные значения, например, х = 2, у = 3 или (х,у) = (2,3),

Вычисляя, получим

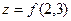= 2∙3 + 2∙2= 10.

Если же эту функцию вычислить при х = 3, у = 2 или (х,у) = (3,2),

то

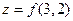= 3∙2 + 2∙3= 12.

Этот пример наглядно показывает важность слов "упорядоченная пара чисел (х, у)". Следует заметить, что для обозначения независимых переменных и функций можно использовать самые разные символы. Рассмотренную выше функцию, например, можно представить, изменив обозначения переменных, как

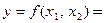
Последнее обозначение особенно удобно. Когда имеется функция п переменных, она обычно обозначается

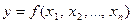
Отличие функции п переменных от функции двух переменных состоит в том, что вместо упорядоченной пары чисел берется упорядоченный набор , которому по определенному правилу ставится в соответствие; единственное число - значение функции.

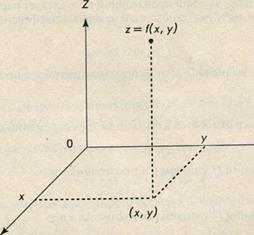
Как известно, функцию одной переменной можно наглядно изобразить в виде графика. В общем случае график функции - это некоторая линия на плоскости. Также существует способ наглядного геометрического представления функции двух переменных. Для этого достаточно две координатные оси Х и У дополнить третьей осью Z, перпендикулярной первым двум (рис. 1). Совокупность точек, построенных для всевозможных значений независимых переменных, представляет собой график функции двух переменных. Обычно это некоторая поверхность в пространстве. К сожалению, для функций более чем двух переменных график наглядно изобразить невозможно.

Рис. 1.

Определение. Функция 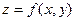называется непрерывной в точке (х 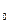, у₀), если она:

1) определена в точке (х₀, у₀);

2) имеет конечный предел пр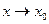и и ;

3) этот предел равен значению функции в точке (х₀, у₀), т.е. .

Геометрический смысл непрерывности очевиден: график в точке (х₀, у₀) представляет собой сплошную, нерасслаивающуюся поверхность.

Частные производные.

Для функции нескольких переменных вводится понятие частной производной по соответствующей переменной. В случае функции двух переменных

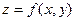
понятие частной производной определяется следующим образом:

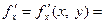
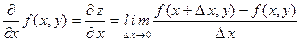
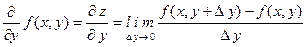
Первая формула определяет частную производную по х, а вторая - частную производную по у.

Вычисление производных от функций нескольких переменных выполняется по обычным правилам дифференцирования функций одной переменной, при этом значения всех переменных. кроме одной, по которой вычисляется производная, считаются постоянными.

Для примера вычислим частные производные функции

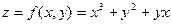
При вычислении частной производной по х следует переменную у считать постоянной, поэтому по обычным правилам дифференцирования имеем::

Аналогично, вычисляя частную производную по у, считаем постоянной переменную х:

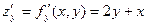
Второй пример относится к функциям трех переменных. Пусть

При вычислении 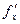считаем у и z постоянными:

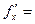
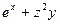
При вычислении 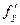считаем постоянными x и z:

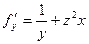
Наконец, считая постоянными х и y, находим :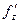

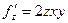
Оба примера наглядно показывают, что частные производные сами являются функциями тех же переменных, от которых эти производные вычислялись. Естественно, как и в случае функции одной переменной, можно определить производные от производных, или производные высших порядков. Мы ограничимся частными производными второго порядка функции двух переменных.

Если частную производную 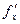продифференцировать по х, а частную производную 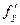продифференцировать по у, получим частные производные второго порядка по х и у:

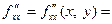
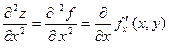
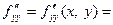
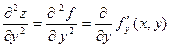
Выше приведены часто употребляющиеся обозначения этих функций.

Если же частную производную 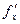продифференцировать по у, а частную производную 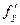продифференцировать по х, получим еще одну пару частных производных второго порядка:

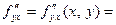
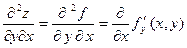
Следует обратить внимание на порядок написания нижних индексов — он соответствует порядку вычисления производных по различным переменным