Неформально предикат можно определить как некоторое высказывание, значение которого зависит от значений предметных переменных из множества M, на котором определен предикат.
Примеры:
a) P(x): “ x есть простое число”;
(Здесь и всюду в дальнейшем для задания предиката будем использовать краткую форму записи, которая подробно расписывается следующим образом: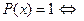 
“ x есть простое число”.)
b) D(x,y): “ x нацело делится на y ”;
c) R(x,y): “ x > y ”.
В качестве предметного множества для этих примеров можно рассматривать любые числовые множества, в частности, в примерах a), b) – M = Í, а в c) – M = Ñ.
Более строго предикат можно определить как отображение n -ной степени множества M, называемой местностью или арностью предиката в двухэлементное множество B = {1, 0}
.
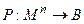При подстановке в предикат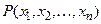 
вместо предметных переменных набора значений 
получим логическое высказывание (так 
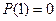, а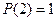 
). Таким образом, предикат представляет собой переменное высказывание (или систему высказываний), истинность которого определяется подстановкой различных значений предметных переменных.
Так как предикаты принимают значения из множества B, то для них определены логические операции 
~. Кроме того, для предикатов вводятся операции утверждения всеобщности и утверждения существования.
Операция утверждение всеобщности ставит в соответствие высказывательной форме P(x) высказывание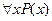 
(читается как, P(x) истинно для всех x из множества M, на котором определен предикат). Высказывание 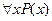истинно тогда и только тогда, когда высказывание P(a) истинно для любого элемента 
.
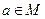Операция утверждение существования ставит в соответствие высказывательной форме P(x) высказывание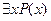 
(читается как, существует такой x из множества M, для которого высказывание P(x) истинно). Высказывание 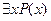истинно тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного элемента .
|
|
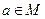Знаки " и $ называются кванторами всеобщности и существование (квантор в переводе с латинского – определение количества). Переход от высказывательной формы P(x) к высказываниям 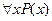или 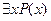называется навешиванием квантора или связыванием переменной x (иногда – квантификацией переменной x). Переменная, на которую навешен квантор, называется связанной, несвязанная переменная называется свободной. Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная – это обычная переменная, которая может принимать различные значения из M, а выражение P(x) – переменное высказывание, зависящее от значения x. 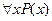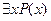Выражения и не зависят от переменной x и при фиксированных P и M имеют вполне определенное значение. Переменные, являющиеся по существу связанными, встречаются не только в математической логике. Например, в выражениях 
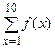или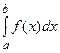 
переменная x связана, при фиксированной f первое выражение равно определенному числу, а второе является функцией от a и b.
Таким образом, в высказываниях 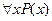и 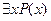говорится не о свойствах отдельных элементов множества M, а о свойствах самого множества M. Истинность или ложность этих высказываний не зависит от того, как обозначена предметная переменная, входящая в них, и ее можно заменить любой другой предметной переменной, например y, и получить высказывания 
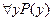и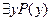 
, имеющие тот же самый смысл и те же самые значения истинности, что и исходные высказывания.
|
|
В общем случае для n -арного предиката, если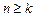 
, операции утверждения всеобщности или существования можно выполнять k раз (порядок выбора переменных, по которым происходит навешивание квантора, может быть любым, исключая их повторение) и получить выражение
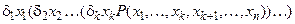, (1)
где 
обозначает квантор всеобщности или существования. Переменные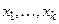 
в высказывательной форме (1) являются связанными, а 
– свободными.
Высказывательная форма (1) при замене переменных элементами множества M обращается в истинное или ложное высказывание. При k = n высказывательная форма (1) становится высказыванием. Изменение порядка следования различных кванторов изменяет смысл высказывания, что может изменить его истинностное значение.
Например, для предиката делимости D(x,y):
высказывание 
читается, как “для любого x существует y, такое, что x делится на y ”, и является истинным высказыванием, так как любое натуральное x делится на себя и на 1, т.е. y = x или y =1;
высказывание 
читается, как “существует y, на который делится любой x ”, и также является истинным высказыванием, так как на значение y =1 делится любое натуральное x.
2. Модель. Формула алгебры предикатов сигнатуры z
Ряд важнейших понятий алгебры предикатов основывается на понятии модели.
Моделью M называется любое множество M с заданными на нем предикатами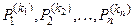 
:
M = < M; >.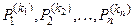
Множество M называется основным множеством модели M, предикаты 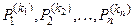– основными предикатами модели M, и их набор z = < 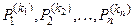> называется сигнатурой модели M. Натуральные числа k 1, ¼, kn обозначают арности соответствующих предикатов, а их набор t = < k 1, ¼, kn > называется типом модели.
|
|
Пример.
N – множество натуральных чисел, E, S, P – определенные на множестве N предикаты равенства, сложения и умножения, т.е.
.
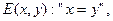
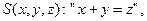
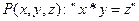Модель M а = < N; E, S, P > является арифметикой натуральных чисел. Ее синатура z = < E, S, P > и тип t = < 2, 3, 3 >.
Любое множество моделей с одной и той же сигнатурой z называется классом Kz моделей сигнатуры z.
Определим формулу алгебры предикатов сигнатуры z. Так же как и в алгебре высказываний, такое определение является индуктивным.
1. Если 
и 
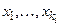– предметные переменные, то выражение 
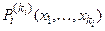есть формула. Такая формула называется атомарной, в ней все вхождения предметных переменных называются свободными.
2. Если U есть формула, в которой имеются свободные вхождения переменной xi, то выражения " xi (U) и $ xi (U) – формулы, в которых все вхождения xi являются связанными, а все вхождения остальных предметных переменных такие же, какими они были в формуле U. При этом формула U называется областью действия соответствующего квантора всеобщности или существования.
3. Если U есть формула, то Ø U – также формула, и все свободные и связанные вхождения предметных переменных в формулу U являются соответственно свободными и связанными вхождениями в формуле Ø U.
4. Если U и V есть формулы, то выражения (U) Ù (V), (U) Ú (V), (U) ® (V), (U) ~ (V) также являются формулами, причем все вхождения предметных переменных в этих формулах такие же, как и в формулах U и V.
5. Формулы могут быть образованы только с помощью правил 1 – 4.
Число скобок в формуле можно уменьшить, если условиться:
не заключать в скобки атомарные формулы и формулы, над которыми записан знак отрицания;
вместо записи 
, где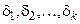 
– некоторые кванторы, допускать запись 
;
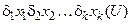не использовать скобки, если порядок выполнения операций соответствует приоритету операций, причем приоритет операций утверждения всеобщности и существования наивысший, для остальных операций такой же, как и в алгебре высказываний;
не заключать в скобки подформулы, обозначенные буквами;
не указывать явно с помощью верхнего индекса местность предиката.
Если формула U не содержит свободных вхождений предметных переменных, то, используя определения операций, можно вычислить ее логическое значение. Если в формуле U есть свободные вхождения предметных переменных, то она является предикатом, называемым формульным, зависящим от значений этих переменных. Но при каждой замене в этой формуле всех свободных вхождений предметных переменных элементами множества M она становится высказыванием, значение которого вычисляется так же, как и в первом случае. Например, формула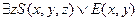 
на модели арифметики натуральных чисел является формульным предикатом от переменных x и y, т.е.
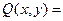
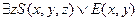(1)
и определяет отношение 
. Легко проверить, что 
, 
, 
.
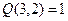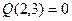Формула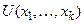 
называется выполнимой на модели M, если для некоторой системы элементов 
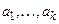модели M сигнатуры z значение формулы 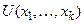сигнатуры z, т.е. высказывание 
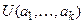, является истинным.
Формула U сигнатуры z называется выполнимой, если существует модель сигнатуры z, на которой выполнима формула U.
Если высказывание 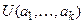является истинным для любой системы значений 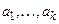Î M, то формула U называется истинной на модели M.
Если формула не выполнима на модели M, то она называется ложной на модели M.
Так формула (1) является выполнимой на модели N, но она не будет ни истинной, ни ложной на ней. Формула
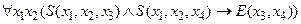
выражает однозначность операции сложения и является истинной на этой модели, а формула 
– ложной.
Если формула U истинна на любой модели класса Kz, то она называется истинной на классеKz.