Транспортная задача
Финансово–экономическая мотивировка
Начнем рассмотрения со следующей финансовой задачи.
Задача об инвестициях. Две компании, реализующие некий инвестиционный проект, должны разместить средства в 40 и 60 (млрд. руб.) в трех банках в размерах 20, 30 и 50 (млрд. руб.) соответственно. При переводе денежных средств компанией 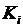 через банк
через банк  уплачивается комиссионный сбор в размере
уплачивается комиссионный сбор в размере  от суммы перевода. Считая известной матрицу комиссии
от суммы перевода. Считая известной матрицу комиссии 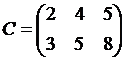 , найти план перевода инвестиций, при котором величина комиссионного сбора будет минимальной. Указать величину комиссии.
, найти план перевода инвестиций, при котором величина комиссионного сбора будет минимальной. Указать величину комиссии.
Всю информацию можно представить в виде таблицы.
| Инвесторы | Банки | Размеры инвестиций | ||
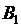
| 
| 
| ||

|

|

|

| |

|

|

|

| |
| Банковские ограничения |
Опишем математическую модель задачи об инвестициях. Пусть переменные  обозначают размер средств, которые переводит
обозначают размер средств, которые переводит  –ый инвестор
–ый инвестор  –му банку. Ясно, что
–му банку. Ясно, что  Нетривиальные ограничения – это система линейных уравнений
Нетривиальные ограничения – это система линейных уравнений
 и
и 
Целевая функция: 
При решении указанной задачи ЛП важную роль играет матрица системы нетривиальных ограничений:
 .
.
Общая постановка задачи
Транспортная задача – задача ЛП, в которой требуется найти оптимальный план транспортировки (однородного) продукта из конечного числа пунктов поставки с заданными объемами производства в конечное число пунктов потребления с известными объемами потребностей при заданной стоимости перевозки единицы транспортируемого продукта между каждой парой пунктов поставки и потребления. Таким образом, оптимальный план должен определять минимальную суммарную стоимость транспортировки, не превышая объем производства каждого из поставщиков и полностью покрывая потребности каждого из потребителей.
Транспортная задача была впервые сформулирована Хитчкоком и с тех пор применяется для решения практических задач доставки и распределения однородных продуктов.
Математическая модель может быть описана следующим образом.
Пусть имеются  поставщиков
поставщиков  и
и  потребителей
потребителей 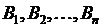 некоторого однородного продукта. Для
некоторого однородного продукта. Для  –го поставщика задан объем производства
–го поставщика задан объем производства  (
( ), а для
), а для  –го потребителя – объем потребления
–го потребителя – объем потребления  (
( ) и известна стоимость доставки единицы продукта
) и известна стоимость доставки единицы продукта  из пункта производства
из пункта производства  в пункт потребления
в пункт потребления  . Переменные
. Переменные  характеризуют объем перевозки между
характеризуют объем перевозки между  –м поставщиком и
–м поставщиком и  –м потребителем. Оптимальный план транспортировки соответствует минимуму линейной целевой функции:
–м потребителем. Оптимальный план транспортировки соответствует минимуму линейной целевой функции:

при ограничениях на потребление и поставку:
 ,
,  .
.
Число базисных переменных в системе ограничений равно 
При целочисленных объемах производства и потребления транспортная задача обладает целочисленным оптимальным планом – это было впервые экспериментально подмечено Данцигом при применении симплекс–метода для решения данной задачи, что позволяет включить транспортную задачу в класс задач целочисленного линейного программирования. Специальные методы, разработанные для решения транспортной задачи, как и симплекс–метод позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Данные обычно представляют в виде транспортной таблицы:
| Поставщики | Потребители | Запасы | |||||
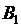
| 
| … | 
| … | 
| ||
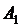
| 
| 
| … | 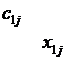
| … | 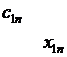
| 
|

| 
| 
| … | 
| … | 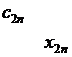
| 
|
| … | … | … | … | … | … | … | … |

| 
| 
| … | 
| … | 
| 
|
| … | … | … | … | … | … | … | … |

| 
| 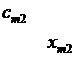
| … | 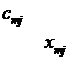
| … | 
| 
|
| Потребности | 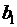
| 
| … | 
| … | 
|
Общее количество товара у поставщиков равно  , а общая потребность в товаре в пунктах назначения есть
, а общая потребность в товаре в пунктах назначения есть  . Если
. Если  , т.е. суммарные запасы поставщиков равны суммарным запросам потребителей, то такая задача называется задачей с правильным балансом, а ее модель – закрытой.
, т.е. суммарные запасы поставщиков равны суммарным запросам потребителей, то такая задача называется задачей с правильным балансом, а ее модель – закрытой.
Критерий разрешимости транспортной задачи. Транспортная задача разрешима только, если она имеет правильный баланс.
В дальнейшем предполагается, если не оговорено противное, что рассматриваемая транспортная задача имеет правильный баланс.
5. Поиск начального опорного плана
В основе решения транспортной задачи с правильным балансом лежит модифицированный симплекс–метод, состоящий из трех основных этапов: а) построение начального опорного плана, б) оценка плана, в) улучшение плана.
Начальным опорным планом называется план перевозок  , который удовлетворяет всем ограничениям транспортной задачи.
, который удовлетворяет всем ограничениям транспортной задачи.
Рассмотрим только один метод построения начального опорного плана – метод минимального тарифа, суть которого состоит в следующем. Начальный опорный план находят, заполняя не более, чем  клеток (по числу базисных переменных). Любое допустимое решение транспортной задачи можно записать в транспортную таблицу. Клетки транспортной таблицы, в которых находятся отличные от нуля (или базисные нулевые) перевозки, называются занятыми, остальные – свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку
клеток (по числу базисных переменных). Любое допустимое решение транспортной задачи можно записать в транспортную таблицу. Клетки транспортной таблицы, в которых находятся отличные от нуля (или базисные нулевые) перевозки, называются занятыми, остальные – свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку  , т.е. стоящая в
, т.е. стоящая в  –ой строке и
–ой строке и  –ом столбце, имеет номер
–ом столбце, имеет номер  . Каждой клетке с номером
. Каждой клетке с номером  соответствует переменная
соответствует переменная  . Выбор заполняемых клеток производят, ориентируясь на тарифы перевозок, а именно: на каждом шаге выбирают какую–нибудь клетку
. Выбор заполняемых клеток производят, ориентируясь на тарифы перевозок, а именно: на каждом шаге выбирают какую–нибудь клетку  , отвечающую минимальному тарифу и помещают в нее максимально возможную перевозку
, отвечающую минимальному тарифу и помещают в нее максимально возможную перевозку  . После этого удаляют либо столбец, либо строку в зависимости от соотношения
. После этого удаляют либо столбец, либо строку в зависимости от соотношения 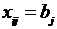 или
или  .
.
Пример 1. Для задачи об инвестициях построить начальный опорный план методом минимального тарифа.
Решение. Транспортная таблица имеет вид
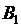
| 
| 
| 
| |
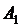
| ||||

| ||||

|
10. Находим наименьший тариф (1,1) и записываем всю потребность  в клетку (1,1), новый запас
в клетку (1,1), новый запас  . В правом нижнем углу стоит контрольное число – общий запас или общая потребность (они равны)
. В правом нижнем углу стоит контрольное число – общий запас или общая потребность (они равны)
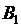
| 
| 
| 
| |
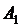
| ||||

| ||||

| – |
20. Полагаем  удаляем столбец
удаляем столбец 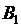 :
:

| 
| 
| |
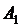
| |||

| |||

|
30. Теперь наименьший тариф находится в клетке (1,2). Записываем весь запас  , т.е. полагаем
, т.е. полагаем  вычисляем новую потребность
вычисляем новую потребность  удаляем строку
удаляем строку 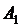 :
:

| 
| 
| |

| |||

|
40. Теперь наименьший тариф находится в клетке (2,2). Записываем потребность  в клетку (2,2), т.е.
в клетку (2,2), т.е.  вычисляем новый запас
вычисляем новый запас  удаляем столбец
удаляем столбец  :
:

| 
| |

| ||

|
50. Осталось заполнить одну клетку; полагаем естественно  Тем самым, опорное решение найдено и может быть можно записано в виде матрицы:
Тем самым, опорное решение найдено и может быть можно записано в виде матрицы:
 .
.
Замечание. В общем случае опорный план транспортной задачи состоит из  занятых клеток (число базисных переменных). Такой план называется невырожденным. Может оказаться, что число занятых клеток опорного плана меньше, чем
занятых клеток (число базисных переменных). Такой план называется невырожденным. Может оказаться, что число занятых клеток опорного плана меньше, чем  (некоторые базисные переменные равны 0) – вырожденный опорный план. В этом случае выбирается одна (или несколько) свободных клеток с наименьшим тарифом, которая в дальнейшем считается занятой с нулевой перевозкой.
(некоторые базисные переменные равны 0) – вырожденный опорный план. В этом случае выбирается одна (или несколько) свободных клеток с наименьшим тарифом, которая в дальнейшем считается занятой с нулевой перевозкой.
Метод потенциалов
Метод потенциалов используется для оценки плана, он основан на следующей теореме.
Теорема. Если допустимое решение  транспортной задачи является оптимальным, то существуют потенциалы поставщиков
транспортной задачи является оптимальным, то существуют потенциалы поставщиков  и потребителей
и потребителей  , удовлетворяющие условиям:
, удовлетворяющие условиям:
 если
если 
 если
если 
Равенства  при
при  используются для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных
используются для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных  и
и  . Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n –1. Так как число неизвестных системы на единицу больше числа уравнений, то одно из них можно задать произвольно (как правило, его берут нулевым), а остальные найти из системы.
. Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n –1. Так как число неизвестных системы на единицу больше числа уравнений, то одно из них можно задать произвольно (как правило, его берут нулевым), а остальные найти из системы.
Неравенства  при
при  используется для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде
используется для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде
 при
при  .
.
Числа 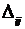 по–прежнему будем называть оценками свободных клеток таблицы, не входящих в базис опорного решения. В этом случае признак оптимальности можно сформулировать так же, как в симплекс–методе (для задачи на минимум): опорное решение является оптимальным, если для всех клеток таблицы оценки неположительные.
по–прежнему будем называть оценками свободных клеток таблицы, не входящих в базис опорного решения. В этом случае признак оптимальности можно сформулировать так же, как в симплекс–методе (для задачи на минимум): опорное решение является оптимальным, если для всех клеток таблицы оценки неположительные.
Пример 2. Является ли оптимальным опорный план, найденный в предыдущем примере?
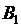
| 
| 
| 
| |
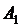
| ||||

| ||||

|
Решение. Определим систему потенциалов, соответствующих опорному решению. Для этого решим систему уравнений  при
при  , считая, что
, считая, что  Находим последовательно
Находим последовательно 

| 
| 
| 
| |

| ||||

| ||||

|
Теперь вычислим оценки всех свободных клеток по формулам  при
при  :
:
 ,
, 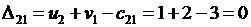
Поскольку  то опорное решение не является оптимальным.
то опорное решение не является оптимальным.
Алгоритм решения транспортной задачи
Оценки для свободных клеток транспортной таблицы используются для улучшения опорного решения. С этой целью находят клетку (l, k) таблицы, соответствующую  . Если
. Если  , то решение оптимальное. Если же
, то решение оптимальное. Если же  , то для соответствующей клетки (l, k) строят цикл и улучшают решение, перераспределяя груз
, то для соответствующей клетки (l, k) строят цикл и улучшают решение, перераспределяя груз  по этому циклу.
по этому циклу.
Определение. Циклом называется такая последовательность клеток транспортной таблицы  , в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце.
, в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце.
Цикл изображают в транспортной таблице в виде замкнутой ломаной линии. В любой клетке цикла происходит поворот звена ломаной линии на 90°.
Простейшие циклы изображены на рис. 1, где кружком отмечены клетки таблицы, включенные в состав цикла. Цикл называется означенным, если его угловые клетки пронумерованы по порядку и нечетным клеткам приписан знак “+”, а четным – знак “–“(рис.2).

 Сдвигом по циклу на величину t называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком “+”, на t и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком “-“, на t.
Сдвигом по циклу на величину t называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком “+”, на t и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком “-“, на t.
Сформулируем теперь алгоритм решения задачи методом потенциалов.
1. Построить начальное опорное решение методом минимального тарифа и проверить правильность его построения (количество занятых клеток должно быть m+n –1). Если количество занятых клеток меньше, то некоторым свободным клеткам необходимо присвоить нулевые перевозки.
2. Записать систему потенциалов, соответствующих опорному решению. Для этого решить систему уравнений  при
при  .
.
Чтобы найти частное решение этой системы, одному из потенциалов (обычно тому, для которого больше занятых клеток) придадим произвольно некоторое значение (как правило, нуль). Остальные потенциалы однозначно определяются по формулам:
 при
при  , если известен потенциал
, если известен потенциал  , и
, и
 при
при  , если известен потенциал
, если известен потенциал  .
.
3. Проверить, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычислить оценки свободных клеток по формулам:
 при
при  ,
,
и те оценки, которые больше нуля, записать в левые нижние углы клеток. Если для всех свободных клеток  , то вычислить значение целевой функции и прервать процесс, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, то перейти к следующему пункту, поскольку опорное решение не является оптимальным.
, то вычислить значение целевой функции и прервать процесс, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, то перейти к следующему пункту, поскольку опорное решение не является оптимальным.
4. Перейти к новому опорному решению, для которого значение целевой функции будет меньше. Для этого найти клетку таблицы, которой соответствует наибольшая положительная оценка  .
.
Построить цикл, включающий данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставить поочередно знаки “+” и “–“, начиная с “+” в клетке с наибольшей положительной оценкой. Выполнить сдвиг по циклу на величину  . Клетка со знаком “–“, в которой достигается
. Клетка со знаком “–“, в которой достигается  , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных записываются базисные нули, чтобы число занятых клеток оставалось равным m+n –1. Затем перейти к п.3
, остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных записываются базисные нули, чтобы число занятых клеток оставалось равным m+n –1. Затем перейти к п.3
Пример 3. Найти методом потенциалов оптимальное решение задачи об инвестициях.
Решение. Начинаем с таблицы, полученной при решении предыдущей задачи:

| 
| 
| 
| |

|

| |||

| ||||

|
10. Рассмотрим цикл  . Вершинам цикла отвечают знаки +,-,+,-. Значит,
. Вершинам цикла отвечают знаки +,-,+,-. Значит, 
Переходим к новому опорному решению:
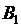
| 
| 
| 
| |
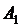
| ||||

| ||||

|
Вычисляем потенциалы 
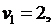


 и оценки свободных клеток:
и оценки свободных клеток:  ,
,  :
:

| 
| 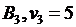
| 
| |

| ||||

|

| |||

|
Поскольку  то опорное решение не является оптимальным.
то опорное решение не является оптимальным.
20. Рассмотрим цикл  . Вершинам цикла отвечают знаки +,-,+,-. Значит,
. Вершинам цикла отвечают знаки +,-,+,-. Значит, 
Переходим к новому опорному решению:
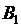
| 
| 
| 
| |
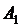
| ||||

| ||||

|
Вычисляем потенциалы: 





| 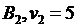
| 
| 
| |

| ||||
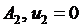
| ||||

|
Теперь вычислим оценки всех свободных клеток:
 ,
, 
Поскольку оценки свободных клеток неположительны, то опорное решение является оптимальным. Оптимальное значение целевой функции равно
 млн. руб.
млн. руб.
Размещение указанных средств происходит с комиссией 
Упражнения
61. Для транспортной таблицы постройте опорное решение методом наименьшего тарифа:
| а) | 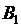
| 
| 
| 
|
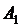
| ||||

| ||||

| ||||

|
| б) | 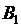
| 
| 
| 
|
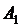
| ||||

| ||||

| ||||

|
| в) | 
| 
| 
| 
| 
|
| |||||

| |||||

| |||||

|
62. Используя метод потенциалов, проверьте оптимальность указанного опорного решения:
| а) | 
| 
| 
| 
| 
|
| |||||

| |||||

| |||||

|
| б) | 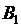
| 
| 
| 
| 
|
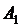
| |||||

| |||||

| |||||

|
63. Для транспортной таблицы:
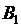
| 
| 
| 
| 
| |
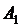
| |||||

| |||||

| |||||

|
найдите оптимальное решение методом потенциалов, используя указанное начальное опорное решение.
64. Найдите оптимальное решение транспортной задачи:
| а) | 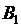
| 
| 
| 
| 
|
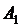
| |||||

| |||||

| |||||

|
| б) | 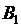
| 
| 
| 
| 
|
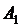
| |||||

| |||||

| |||||

|
| в) | 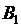
| 
| 
| 
| 
|
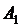
| |||||

| |||||

| |||||

|
| г) | 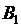
| 
| 
| 
| 
|
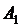
| |||||

| |||||

| |||||

|
65. Найдите а) ранг матрицы системы ограничений; б) число базисных переменных в системе ограниченийтранспортной задачи с параметрами  ,
,  .
.
66. Постройте нецелое опорное решение транспортной задачи с параметрами 
67. Докажите, что если 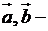 двумерные векторы с целыми координатами, то оптимальное решение транспортной задачи с правильным балансом также является целым.
двумерные векторы с целыми координатами, то оптимальное решение транспортной задачи с правильным балансом также является целым.