Задачи 11-20
Даны координаты вершин пирамиды:

Требуется найти:
1) Вектор 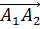 (его длину и направление);
(его длину и направление);
2) Угол между векторами 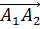 и
и  ;
;
3) Уравнение грани 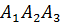 ;
;
4) Площадь грани 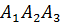 ;
;
5) Угол между ребром  и гранью
и гранью 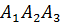 ;
;
6) Уравнение прямой  ;
;
7) Объем пирамиды.
 Сделать чертеж.
Сделать чертеж.
Пример решения задачи, аналогичной задачам №1-10.
При 
1.1 Изображаем чертеж пирамиды по заданным точкам  с указанием векторов
с указанием векторов 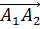 ,
,  ,
, 
1.2 Находим координаты векторов 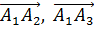 ,
,  , которые равны проекциям этих векторов на координатные оси:
, которые равны проекциям этих векторов на координатные оси:

Аналогично:


1.3 Определяем длины векторов  ,
, 


1.4 Вычисляем направляющие косинусы углов между вектором 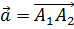 и ортами осей координат. Указанные углы определяют направление вектора
и ортами осей координат. Указанные углы определяют направление вектора 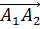 в аналитической форме.
в аналитической форме.
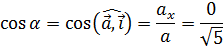

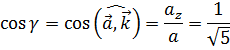
Замечание! На чертеже углы α, β, γ показаны относительно осей  ,
,  ,
, 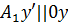 , так как при параллельном переносе осей указанные углы не изменяются
, так как при параллельном переносе осей указанные углы не изменяются
2. Находим угол между векторами  и
и  , используя скалярное произведение векторов.
, используя скалярное произведение векторов.
В общем случае 
В данном примере:


3. Определяем уравнение грани 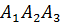 . Грань
. Грань 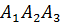 (на чертеже заштрихована) является частью плоскости, проходящей через заданную точку
(на чертеже заштрихована) является частью плоскости, проходящей через заданную точку  .
.
Тогда уравнение плоскости в общем виде можно представить так:

Векторы  и
и 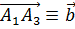 лежат в указанной плоскости. Вектор нормали к плоскости
лежат в указанной плоскости. Вектор нормали к плоскости  ортогонален плоскости и векторам
ортогонален плоскости и векторам  и
и  , лежащим в этой плоскости. Поэтому
, лежащим в этой плоскости. Поэтому  .
.
В данном примере:
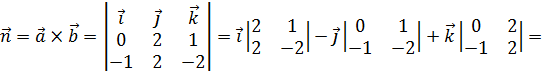


Тогда уравнение грани  , как плоскости, проходящей через точку
, как плоскости, проходящей через точку  с нормалью
с нормалью  , будет иметь вид:
, будет иметь вид:

 .
.
Примечание. Для проверки рекомендуется определить уравнение грани
как плоскости, проходящей через три заданные точки А  ,А
,А  ,А
,А  .
.
4. Находим площадь грани  , используя векторное произведение векторов
, используя векторное произведение векторов  и
и  .
.  Это произведение по модулю равно площади параллелограмма, построенного на этих векторах. Площадь грани А
Это произведение по модулю равно площади параллелограмма, построенного на этих векторах. Площадь грани А  А
А  А
А  составляет половину этой площади
составляет половину этой площади  .
.


5. Находим угол между ребром  и гранью
и гранью  ,поэтому, искомый угол находят по формуле:
,поэтому, искомый угол находят по формуле:


Ребро  перпендикулярно грани
перпендикулярно грани  .
.
6. Определяем уравнение прямой  . Прямая проходит через точку
. Прямая проходит через точку  и совпадает с линией действия вектора
и совпадает с линией действия вектора  . Тогда, принимая вектор
. Тогда, принимая вектор  за направляющий вектор прямой, можно записать каноническое уравнение прямой
за направляющий вектор прямой, можно записать каноническое уравнение прямой  :
:

В данном примере 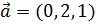 , точка
, точка 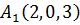 . Тогда каноническое уравнение прямой
. Тогда каноническое уравнение прямой  имеет вид:
имеет вид:

Общее уравнение прямой в пространстве имеет вид: 
7. Находим объем пирамиды  .
.
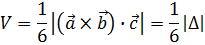



Задачи № 21-30
Эти задачи на составление уравнений прямых на плоскости, удовлетворяющих заданным условиям, не имеют общего алгоритма решения.
При их решении необходимо использовать основные расчетные формулы и комбинации известных решений основных задач для прямых на плоскости. (см., например, Вылегжанин И.А., Пожидаев А.В., Остроменский П.И. и др. Практикум по высшей математике для технических специальностей. Часть 1 – Новосибирск: Изд-во СГУПСа, 2011. – 228с. – с. 146-153.)
Рассмотрим решения некоторых задач, аналогичных задачам №11-20 КР-1.
Задача 1. Составить уравнение прямой, проходящей через точку пересечения прямых  перпендикулярно прямой
перпендикулярно прямой  .
.
Решение. Находим координаты точки пересечения прямых из решения системы линейных уравнений (СЛАУ):

Решаем СЛАУ по формулам Крамера: 


Точка пересечения прямых – т.  принадлежит прямой, уравнение которой необходимо найти. Поэтому уравнение искомой прямой будем искать в виде
принадлежит прямой, уравнение которой необходимо найти. Поэтому уравнение искомой прямой будем искать в виде 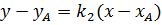 .
.
Прямые ортогональны по условию, поэтому, угловой коэффициент  , где
, где  - угловой коэффициент прямой
- угловой коэффициент прямой  . При этом
. При этом  . Тогда
. Тогда  и уравнение искомой прямой будет иметь вид:
и уравнение искомой прямой будет иметь вид:

Задача 2. Дан треугольник с вершинами:  .
.
Необходимо составить уравнения стороны 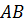 , высоты
, высоты  и медианы
и медианы  . Показать чертеж.
. Показать чертеж.
Решение. Строим чертеж треугольника 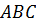 .
.
 Коэффициенты точек
Коэффициенты точек  известны. Уравнение прямой
известны. Уравнение прямой 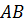 найдем как уравнение прямой, проходящей через две точки.
найдем как уравнение прямой, проходящей через две точки.

 - уравнение стороны
- уравнение стороны 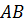 .
.
Высоту  как прямую, проходящую через точку
как прямую, проходящую через точку 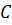 , можно представить уравнением
, можно представить уравнением  .
.
Уравнение прямой 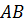
 известно, поэтому угловой коэффициент этой прямой
известно, поэтому угловой коэффициент этой прямой  . Прямые
. Прямые 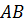 и
и  перпендикулярны
перпендикулярны  , поэтому
, поэтому  . Таким образом, уравнение высоты
. Таким образом, уравнение высоты  будет иметь вид:
будет иметь вид:
 .
.
Точка  делит сторону
делит сторону 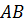 пополам. Координаты точки
пополам. Координаты точки  равны:
равны:
 .
.
Уравнение медианы:

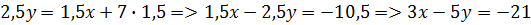
Задача 3. Даны две смежные вершины параллелограмма  пересечения диагоналей. Найти две другие вершины параллелограмма. Построить параллелограмм.
пересечения диагоналей. Найти две другие вершины параллелограмма. Построить параллелограмм.
Решение. Точка пересечения диагоналей  делит диагонали пополам.
делит диагонали пополам.




Аналогично 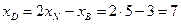

Уравнения диагоналей  можно представить так:
можно представить так:



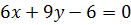
 - уравнение диагонали
- уравнение диагонали 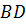
Аналогично найдем уравнение диагонали 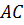 .
.
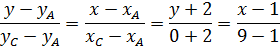
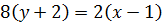

Окончательно уравнение диагонали 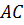 будет иметь вид:
будет иметь вид:
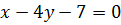
Задачи № 31-40
В указанных задачах необходимо составить уравнения линий на плоскости (прямых или кривых второго порядка), соответствующих заданным условиям.
В силу большого разнообразия условий, которым должны удовлетворять искомые линии, единый алгоритм решения таких задач отсутствует.
Уравнения линий можно получить из соотношений для расстояний, связывающих заданные фиксированные точки и текущую точку линии.
Рассмотрим решения задач, аналогичных задачам, заданным в КР-1.
Задача 1. Составить уравнение линии, равноудаленной от двух данных точек 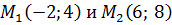 .
.
Решение. Пусть точка  текущая точка искомой линии. Определяем расстояния
текущая точка искомой линии. Определяем расстояния  и приравниваем их:
и приравниваем их:




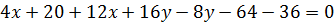


Таким образом, множество текущих точек  , удовлетворяющих условиям задачи, является прямой линией.
, удовлетворяющих условиям задачи, является прямой линией.
Задача 2. Составить уравнение линии, каждая точка из которой удалена от точки 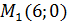 втрое дальше, чем от точки
втрое дальше, чем от точки  .
.
Решение. Пусть точка  - текущая точка искомой линии. По условию
- текущая точка искомой линии. По условию  .
.


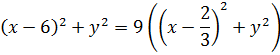

После упрощения полученного равенства получим уравнение окружности  с центром в начале координат.
с центром в начале координат.
Задачи № 41-50
Задача. Дано алгебраическое уравнение линии

Это уравнение необходимо привести к каноническому виду. Затем в старой (исходной) системе координат построить каноническую систему координат и кривую линию по каноническому уравнению.
Решение. Используя способ дополнения до полного квадрата, преобразуем заданное уравнение к почти - каноническому виду.
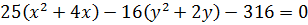




Полученно почти – каноническое уравнение гиперболы в «старой» (исходной) системе координат. Центр симметрии гиперболы в этой системе координат смещен и находится в точке  .
.
Если принять  , то в новой (канонической) системе координат XOY каноническое уравнение гиперболы будет иметь вид
, то в новой (канонической) системе координат XOY каноническое уравнение гиперболы будет иметь вид

Построение гиперболы начинаем с изображения двух систем координат: исходной («старой») Cxy и параллельно-смещенной «новой» (канонической) системы координат OXY.
В новых осях OXY строим прямоугольник со сторонами  , где a и b – длины полуосей гиперболы.
, где a и b – длины полуосей гиперболы.  .
.
Диагонали параллелограмма являются асимптотами для ветвей гиперболы. При  ветви гиперболы неограниченно приближаются к асимптотам.
ветви гиперболы неограниченно приближаются к асимптотам.
Вершины ветвей гиперболы (точки  ) лежат в точках пересечения оси OX вертикальными сторонами прямоугольника.
) лежат в точках пересечения оси OX вертикальными сторонами прямоугольника.
Учитывая, что гипербола имеет центр симметрии, находим координаты промежуточных точек:
При 
В результате имеем точки  и
и 
При 
Тогда получим точки  и
и 
По найденным точкам строим ветви гиперболы, плавно приближая их к наклонным асимптотам после точек 

Тема 3. Пределы и производные функций
Примеры решения задач, аналогичных задачам 51-60
Необходимо найти пределы нижеследующих функций одной переменной (без правила Лопиталя).
а) 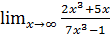
б) 
в) 
г) 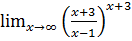
Пример а) 
Решение. Определяем вид неопределенности. При формальных операциях с бесконечностями обращаемся с ними как с бесконечно большими функциями.


Бесконечно малыми функциями  пренебрегаем, так их пределы всегда равны нулю. При формальных операциях с нулями обращаемся с ними как с бесконечно малыми.
пренебрегаем, так их пределы всегда равны нулю. При формальных операциях с нулями обращаемся с ними как с бесконечно малыми.
Пример б)


Пример в)


Пример г)
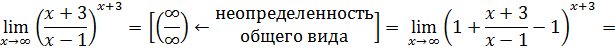



Проверка с помощью правила Лопиталя двух пределов (производится после выполнения нижеследующих задач №11-20 (КР-2).
Правило Лопиталя применяют для раскрытия неопределенностей  с использованием дифференцирования функций.
с использованием дифференцирования функций.
Пример а)


Пример в) 

Задачи №61-70
Необходимо найти производные первого порядка функций одной переменной, используя правила дифференцирования и формулы дифференцирования основных элементарных функций (табличных производных).
Примеры решения конкретных задач, аналогичных задачам №11-20 (КР-2):
а) 
б) 
в) 
г) 
д) 
Пример а) 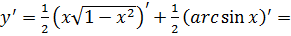


Пример б) 
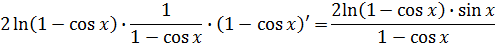
Пример в) 
Пример г) 
Решение. Дана функция одной переменной в неявной форме. В этом случае при дифференцировании переменной y по x, эту переменную рассматривают как сложную функцию аргумента x (например,  .
.
В нашем примере получим:
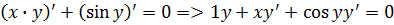

Пример д) 
При дифференцировании функций, содержащих несколько сомножителей в числителе и знаменателе или показательно-степенных функций вида y=f(x)φ(x), функции сначала логарифмируют, а затем дифференцируют.





Задачи №71-80
Найти производные  для заданных функций. Часть функций задана в параметрической форме x=x(t), y=y(t).
для заданных функций. Часть функций задана в параметрической форме x=x(t), y=y(t).
Производные первого и второго порядков для таких функций определяются по формулам
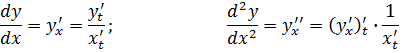
Примеры решения конкретных задач аналогичных задачам №21-30 (КР-2).
а)  б)
б) 
Найти производные  и
и 
Решение.
Пример а) 
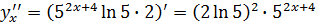
Пример б) 


Задачи 81-90
Необходимо построить график функции y=f(x), используя общую схему исследования функции, включающую следующие пункты:
1. Найти область существования (естественного определения функции).
2. Проверить является ли функция симметричной относительно оси Oy (четной) или относительно начала координат (нечетной), или периодической.
3. Найти точки разрыва функции, точки пересечения графиком функции осей координат и определить интервалы знакопостоянства функции способом пробных точек.
4. Найти асимптоты графика функции (вертикальные, наклонные, горизонтальные); при наличии асимптот определить асимптотическое поведение функции с помощью односторонних пределов; при отсутствии указанных асимптот исследовать поведение функции в граничных точках области существования, включая  .
.
Замечание. Пункты (П) 1-4 выполняются без использования производных.
5. Находим критические точки первого и второго рода и определяем значения функции в этих точках.
6. Разбить область существования на частичные интервалы, разделенные точками разрыва, нулями функции, критическими точками первого и второго рода.
7. Исследовать монотонность (убывание – возрастание) и выпуклость функции в выделенных интервалах. Определить наличие экстремумов в критических точках первого рода двумя способами. Найти точки перегиба среди критических точек второго рода.
8. Результаты исследования представить в табличной форме и в виде графика.
Дана функция  . Необходимо построить график функции, используя общую схему ее исследования.
. Необходимо построить график функции, используя общую схему ее исследования.
П-1. Функция не имеет точек разрыва, так как существует при всех значениях аргумента  . Поэтому область существования – вся числовая ось
. Поэтому область существования – вся числовая ось  .
.
П-2. Функция не удовлетворяет условиям четности  , нечетности
, нечетности  и периодичности
и периодичности  . Она является функцией общего вида и ее необходимо исследовать при всех значениях аргумента.
. Она является функцией общего вида и ее необходимо исследовать при всех значениях аргумента.
П-3. Определяем, имеет ли функция асимптоты. Вертикальные асимптоты отсутствуют, так как функция не имеет точек разрыва. Определяем наклонную асимптоту y=kx+b. Если хотя бы один из коэффициентов (k, b) равен  , то наклонная асимптота отсутствует. В нашем примере
, то наклонная асимптота отсутствует. В нашем примере

Так как угловой коэффициент  , то наклонная и горизонтальные асимптоты отсутствуют.
, то наклонная и горизонтальные асимптоты отсутствуют.
Исследуем поведение функции при  .
.

Аналогично исследуется поведение функции при  .
.
Из проведенных исследований следует, что значения функции при  неограничены.
неограничены.
П-4. Находим нули функции из уравнения  . Из алгебры многочленов известно, что, если многочлен с целыми коэффициентами и единичным коэффициентом при
. Из алгебры многочленов известно, что, если многочлен с целыми коэффициентами и единичным коэффициентом при  имеет целые корни, то они являются делителями его свободного члена.
имеет целые корни, то они являются делителями его свободного члена.
В нашем примере многочлен  содержит целые коэффициенты при неизвестных; свободный член равен 6 и имеет следующие делители
содержит целые коэффициенты при неизвестных; свободный член равен 6 и имеет следующие делители  . Некоторые из этих делителей будут корнями многочлена.
. Некоторые из этих делителей будут корнями многочлена.
Методом пробных точек находим один корень.
При 
При 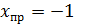

Таким образом, находим первый корень многочлена  . Тогда, разделив исходный многочлен на одночлен
. Тогда, разделив исходный многочлен на одночлен  , получим
, получим

Находим еще два корня многочлена  и
и  из решения квадратного уравнения
из решения квадратного уравнения 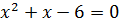 .
.
Таким образом, график функции пересекает ось Ox в трех точках  ,
,  ,
,  . Ось Oy график функции пересекает в одной точке (при
. Ось Oy график функции пересекает в одной точке (при  .
.
Область существования функции  разделяется на интервалы знакопостоянства нулями функции. При этом знаки функции в указанных интервалах определяем методом пробных точек.
разделяется на интервалы знакопостоянства нулями функции. При этом знаки функции в указанных интервалах определяем методом пробных точек.
Интервал 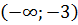 . В пробной точке
. В пробной точке  значения функции
значения функции

Таким образом, во всех точках интервала 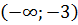 функция отрицательна.
функция отрицательна.
Аналогично определяем, что во втором интервале  функция положительна; в интервале
функция положительна; в интервале  функция отрицательна, в интервале
функция отрицательна, в интервале  - положительна. Полученные результаты рекомендуется отразить в графической форме на числовой оси Ох.
- положительна. Полученные результаты рекомендуется отразить в графической форме на числовой оси Ох.
П-5. Вычисляем производные функции

При  получаем из
получаем из  координаты критических точек первого рода (точек стационарности).
координаты критических точек первого рода (точек стационарности).

Аналогично из уравнения 
 получаем критическую точку второго рода
получаем критическую точку второго рода

Находим значение функции в критических точках.





П-6. Разбиваем область существования функции на отдельные непересекающиеся интервалы характерными точками: нулями функции  критическими точками первого рода
критическими точками первого рода
 и второго рода
и второго рода  .
.
В результате получаем следующие интервалы: 
 .
.
П-7. Определяем свойства функции в интервалах (П-6.)
Первый интервал 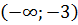 . Функция отрицательна (см. П-4.). Выбираем пробную точку внутри интервала
. Функция отрицательна (см. П-4.). Выбираем пробную точку внутри интервала  и определяем знак первой производной
и определяем знак первой производной

Отсюда следует, что функция в данном интервале возрастает.

Таким образом, в первом интервале функция отрицательна, возрастает и имеет выпуклость вверх.
Второй интервал  . Функция положительна (см. П-4.). Выбираем пробную точку
. Функция положительна (см. П-4.). Выбираем пробную точку  и определяем знак первой производной
и определяем знак первой производной
 функция возрастает.
функция возрастает.
 функция выпукла вверх.
функция выпукла вверх.
В правой окрестности второго интервала лежит критическая точка  . Исследуем ее на наличие экстремума первым и вторым способом.
. Исследуем ее на наличие экстремума первым и вторым способом.
Первый способ. Слева от критической точки 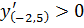 , справа в пробной точке
, справа в пробной точке 

Первая производная функции имеет разные знаки слева и справа от критической точки  . Значит в этой точке экстремум – максимум, потому что слева
. Значит в этой точке экстремум – максимум, потому что слева 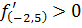 , а справа
, а справа  .
.
Проверяем наличие экстремума вторым способом с помощью второй производной  - в критической точке имеем максимум.
- в критической точке имеем максимум.
Для остальных интервалов и критических точек проводятся аналогичные исследования. Результаты исследований сводятся в таблицу.
Таблица
| Характерные точки и интервалы | Знак и числовые значения функции | Знак первой производной | Знак второй производной | Краткая характеристика поведения функции |
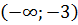
| <0 | >0 | <0 | Отрицательная, возрастает, выпуклость вверх |
| x=-3 | - | - | Нуль функции | |

| + | >0 | <0 | Положительная, возрастает, выпуклость вверх |
| x=-2,118 | +4,06 | <0 | Критическая точка первого рода – точка максимума | |

| >0 | <0 | <0 | Положительная, убывает, выпуклость вверх |
| x=-1 | - | - | Нуль функции | |
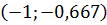
| <0 | <0 | <0 | Отрицательная, убывает, выпуклость вверх |
| x=-0,667 | -2,071 | - | - | Критическая точка второго рода – точка перегиба |

| <0 | <0 | >0 | Отрицательная, убывает, вогнутость |
| x=0,786 | -8,06 | - | Критическая точка первого рода – точка минимума | |

| <0 | >0 | >0 | Отрицательная, возрастает, вогнутость |
| x=2 | - | - | Нуль функции | |
 . .
| >0 | >0 | >0 | Положительная, возрастает, вогнутость |
П-8. Строим график функции, используя табличные данные
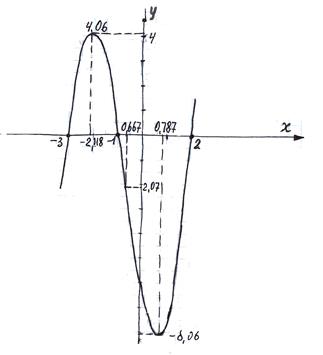
Проверяем соответствие графика функции её свойствам, приведенным в таблице