В.В. Михайлов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям
по курсу
«Основы теории подобия и размерностей»
Методические указания рассмотрены и утверждены на заседании кафедры,
«_ 20 _» __ 11 ___ 2009 г. протокол №_ 4 __
РЫБИНСК 2009
УДК 536.7:536.24
Основы теории подобия и размерностей: Программа учебной дисциплины и методические указания к выполнению контрольной работы / сост. В.В. Михайлов; РГАТА. – Рыбинск, 2009. – 24 с. (Заочная форма обучения / РГАТА).
Данные методические указания предназначены для выполнения контрольных работ студентами специальности 140106, 160301,140106.
СОСТАВИТЕЛЬ
кандидат технических наук, доцент В.В. Михайлов
ОБСУЖДЕНО
на заседании кафедры «Авиационные двигатели»
РЕКОМЕНДОВАНО
Методическим Советом РГАТА
ВВЕДЕНИЕ
Настоящие методические указания по учебной дисциплине «Основы теории подобия и размерностей» предназначены для студентов по специальности 140106 «Энергообеспечение предприятий», 160301 «Авиационные двигатели и энергетические установки». Программа курса составлена в соответствии с учебным планом и Государственным общеобразовательным стандартом высшего профессионального образования.
Целью преподавания дисциплины является более углубленное изучение основ теории подобия и размерностей, как дисциплины о характерных для каждого данного физического процесса обобщенных переменных. Изучение методов построения и применения этих переменных в практике экспериментальных исследований.
В процессе изучения дисциплины должны быть решены следующие задачи:
– формирование логически обоснованного массива теоретических знаний с учетом фактора единства теории и практики;
– изучение фактора взаимосвязи с другими специальными учебными дисциплинами;
– применение полученных знаний и навыков студентами при решении практических задач.
Изучение дисциплины "Основы теории подобия и размерностей" базируется как на фундаментальных дисциплинах: «Высшая математика», «Физика», так и на общетехнических: «Механика жидкостей и газов», «Термодинамика» и других дисциплинах. Рассмотрение ряда вопросов невозможно без применения, достаточных знаний и по информатике. Таким образом, необходимы сведения почти из всех дисциплин, предусмотренных учебным планом.
Учебный материал дисциплины «Основы теории подобия и размерности» достаточно полно изложен в учебниках списка основной литературы. Дополнительная литература рекомендуется для более глубокой проработки отдельных разделов программы и лучшего освоения материала.
Изучение дисциплины рекомендуется проводить последовательно в порядке перечисления разделов рабочей программы.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
1.Элементы теории размерности.
1.1. Единицы измерения
Измерить какую-либо величину Q – это значит сравнить ее с другой величиной q той же физической природы, т. е. определить, во сколько раз Q больше q. Для единообразия устанавливают (в масштабе страны, континента, всего мира) определенное значение величины q и называют ее единицей измерения. Так, за единицу длины (метр) принимается длина 1650763,33 волн излучения атома криптона, за единицу времени (секунда) принимается определенная часть года и т. д.
Единицы измерения различных физических величин, объединенные на основе их непротиворечивости друг другу, образуют систему единиц. Наиболее распространенной и имеющей предпочтительное применение является Международная система единиц (СИ) (System International).
В СИ произвольно, т. е. независимо одна от другой, выбраны единицы измерения так называемых первичных величин — массы (килограмм, кг), длины (метр, м), времени (секунда, сек), силы тока (ампер, А),температуры (Кельвин, К) и силы света (Канделла). Они получили название основных единиц.
Единицы измерения остальных, вторичных, величин выражаются через основные. Формула, указывающая зависимость единицы измерения вторичной величины от основных единиц измерения, называется размерностью этой величины. Размерность вторичной величины находится при помощи определительного уравнения, служащего определением этой величины в математической форме. Например, определительным уравнением для скорости является
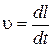
Будем указывать размерность величины при помощи взятого в квадратные скобки символа этой величины, тогда
[ u ]=[ L ][ T ]-1,
где [ L ], [ Т ]– соответственно размерности длины и времени;
Определительным уравнением для силы можно считать второй закон Ньютона F = mа.
Тогда [ F ] = [ M ][L][ T ]-2.
Определительное уравнение работы A=Fs;
[ A ] = [ M ][ L ]2[ T ]-2.
Необходимо отметить одно существенное обстоятельство: размерность любой физической величины представляет собой произведение возведенных в степень размерностей первичных величин.
Так в случае трех основных единиц измерения [ Q ] = [ M ] m [ L ] l [ T ] τ.
1.2. Переход от одних единиц измерения к другим
При решении какой-либо задачи очень редко бывает так, что имеются шесть основных единиц измерения. Например, если изучается поведение чисто механической системы, то такие единицы, как ампер, Кельвин, свеча, не входят в размерность ни одной величины, размерность любой вторичной величины выражается через метр, килограмм, секунду. Электрическая система, в которой отсутствует механическое перемещение тел, определяется размерностями тока, длины, времени (ампер, метр, секунда).
Будем иметь в виду только механические системы с их тремя основными единицами измерения. Легко заметить, что общность получаемых ниже выводов от этого не теряется. Как известно, этими тремя основными единицами являются единицы измерения длины [ L ], массы [ М ] и времени [ Т ].
Можно ли выбрать в качестве первичных величин какие-либо три иные: u 1; u 2; u 3?
Очевидно, это можно сделать в том случае, если:
1) размерности [ u 1], [ u 2], [ u 3]являются независимыми функциями [ М ], [ L ],[ T ], т. е. [ u 1] ¹ [ u 3]a [ u 2]b,при любых a и b;
2) возможно однозначное обратное преобразование, т. е. [ М ], [ L ], [ Т ]единственным образом можно выразить через [ u 1], [ u 2], [ u 3].
Выясним, при каком условии оба эти требования удовлетворяются.
Пусть размерности u 1, u 2, u 3таковы:
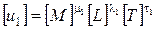 ,
, 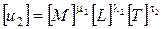 ,
, 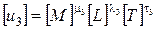 .
.
Прологарифмируем эти выражения
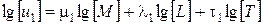 ;
;
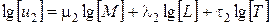 ;
;
 .
.
Как известно из курса алгебры, такая система уравнений имеет решение, и притом единственное, если составленный из коэффициентов уравнения определитель отличен от нуля:
 .
.
Тем самым удовлетворяется второе требование, т. е. при выполнении условия 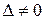 [ М ], [ L ], [ Т ]единственным образом выражается через [ u 1], [ u 2], [ u 3].
[ М ], [ L ], [ Т ]единственным образом выражается через [ u 1], [ u 2], [ u 3].
В то же время условие 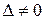 указывает на независимость функций через [ u 1], [ u 2], [ u 3]. Действительно, если бы имелось равенство
указывает на независимость функций через [ u 1], [ u 2], [ u 3]. Действительно, если бы имелось равенство
[ u 1] = [ u 2]a [ u 3]b.
откуда
lg [ u 1] = a lg [ u 2] + b lg [ u 3],
то тогда
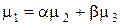 ,
, 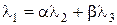 ,
, 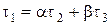 ,
,
т.е. первая строка определителя являлась бы линейной комбинацией второй и третьей, и определитель равнялся бы нулю, что противоречит условию (1).
Итак, условием возможности выбора в качестве основных единиц через [ u 1], [ u 2], [ u 3]является условие 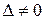 .
.
Полученное правило, очевидно, характерно и для более общего случая при любом числе основных единиц. При этом, если число основных единиц равно 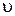 , то количество величин ui также равно
, то количество величин ui также равно 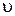 , порядок определителя
, порядок определителя  будет
будет 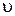 .
.
Например, первичными величинами могут быть сила, время, длина (система МКГСС):
u l = F, u 2 = T, u 3 = L;
действительно, соответствующий определитель
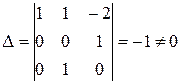
Первичными величинами могут быть и сила, плотность, время, поскольку соответствующий определитель D= – 4. Но для силы, скорости и мощности D=0, эти величины не являются независимыми (что можно усмотреть и из связывающего их уравнения N = F 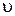 ),и их размерности не могут быть использованы в качестве основных единиц измерения.
),и их размерности не могут быть использованы в качестве основных единиц измерения.
2. Основные теоремы теории подобия.
2.1. Понятие подобия
Обозначим словом система совокупность физических объектов (элементов системы), объединенных на основе некоторого признака, индивидуализирующего набор данных элементов и сообщающего системе определенные качества. Будем иметь в виду такие системы, состояние которых является однозначной функцией состояний отдельных элементов.
Параметрами системы назовем величины, характеризующие ее элементы и воздействующие на нее внешние объекты, т.е. величины, выделяющие каждый объект из множества других той же физической природы; обобщенные координаты системы — величины, описывающие поведение системы — их количество равно числу степеней свободы системы.
Обобщенные координаты могут изменяться с течением времени, или от точки к точке. Например, для системы: груз массой m,колеблющийся на пружине жесткости с при ускорении свободного падения g,обобщенной координатой, является отсчитываемое от некоторого начального положения вертикальное смещение груза х,параметры m, g, с. Измножества параметров данной системы выделим минимально возможное количество параметров, достаточное для однозначного определения состояния системы; эти параметры между собой независимы, назовем их основными, или определяющими.
Пусть имеются две системы одинаковой физической природы, состоящие из одинакового числа аналогичных элементов, которые играют в обеих системах одинаковую роль. Одну систему назовем модель, другую систему — натура, относящиеся к ним величины обозначим соответственно индексами м, н.
Система определяется s независимыми (основными) параметрами pk и имеет п независимых обобщенных координат 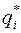 . Время и начальные условия включим в число параметров и условимся, что индекс i имеет значения 1, 2, ..., п,а индекс k — значения п+ 1,..., n + s.
. Время и начальные условия включим в число параметров и условимся, что индекс i имеет значения 1, 2, ..., п,а индекс k — значения п+ 1,..., n + s.
Обобщенные координаты этих систем являются одинаковыми функциями параметров:
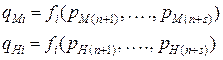 .
.
Вообще 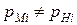 ;
;  .
.
Две системы называют подобными, если их любые две соответствующие обобщенные координаты для любых сходственных моментов времени (сходственных точек пространства) пропорциональны, т. е. две системы подобны, если
 ,
,
где qсi = const, tн = tctМ, tc = const, tн, tM – сходственные моменты времени.
Таким образом, если известно, что две системы подобны и можно найти коэффициенты подобия qсi, то, зная поведение одной системы (модели), можно знать и то, как будет вести себя другая система (натура).
Примером подобия систем может служить один из наиболее простых, но часто встречающихся на практике случаев. Две механические системы, для любых двух соответствующих точек которых справедливы равенства
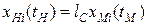 ,
,  ,
, 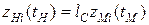 ,
,
очевидно, будут подобными (такие системы называют еще кинематически подобными). В данном случае обобщенными координатами являются, декартовы, коэффициенты подобия для всех координат одинаковы.
Если между точками систем существует еще материальное подобие, т.е. 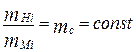 , то системы называют динамически подобными. При наличии динамического подобия легко устанавливается связь между всеми кинематическими и динамическими характеристиками систем. Так, для скоростей характерна связь
, то системы называют динамически подобными. При наличии динамического подобия легко устанавливается связь между всеми кинематическими и динамическими характеристиками систем. Так, для скоростей характерна связь
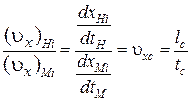 ;
;
аналогично
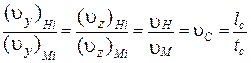 ;
;
для ускорений
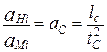 ;
;
для сил
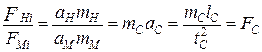 ;
;
и так далее.
При динамическом подобии систем коэффициенты подобия различных величин выражаются через исходные коэффициенты подобия тС, l с, tc – при помощи формул размерности этих величин:
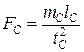 ;
; 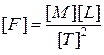 ;
;
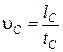 ;
; 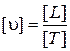 .
.
Часто коэффициенты подобия одних вторичных величин удобно выражать через коэффициенты подобия других вторичных величин. Например,
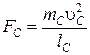 .
.
Если же плотность соответствующих частей обеих систем одинакова, т.е.
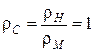 ,
,
то  и
и  .
.
2.2. Необходимые и достаточные условия подобия
Теорема: достаточным условием подобия двух систем является равенство любых двух соответствующих критериев подобия этих систем, составленных из их основных параметров и начальных (граничных) условий.
Теорема указывает, каковы должны быть системы, чтобы между ними существовало подобие.
Чтобы создаваемая машина или имитируемое явление были подобны модели, нужно:
1) выбрать s определяющих параметров, включая в них начальные (граничные) условия и, если необходимо, время, и составить из них s – r независимых критериев подобия;
2) выбрать параметры натуры так, чтобы ее критерии были такие же, как у модели:  ,
, 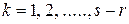 .
.
Причем условие  принято выражать так:
принято выражать так:
Пk = idem
(idem означает такой же, одно и то же).
Выполненным выше операциям можно дать следующее толкование: примем некоторую систему за модель и выберем ее параметры М, L, Т в качестве первичных величин, благодаря чему получим основные единицы [ М ],[ L ], [ Т ].
Тогда числовое значение относящихся к натуре величин можно получить, измерив все соответствующие величины модели в системе единиц [ mM ], [ lL ], [ tT ];в таком случае модель и натура подобны. Действительно,
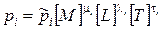 ,
, 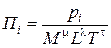 ,
,
 .
.
Отсюда видно, что при выборе на основе модели значений для величин натуры произвольные значения можно придать лишь стольким величинам натуры, сколько имеется основных единиц измерения (точнее – каков ранг матрицы).
Предположим теперь, что подобие между системами имеется заведомо. Каковы в таком случае необходимые условия подобия?
Здесь возможны два случая.
1. Рассмотрим теперь системы, в которых, каждому значению qi соответствует только один набор параметров рк,т. е. связь между обобщенными координатами и параметрами взаимно однозначная.
Поскольку подобие между моделью и натурой заведомо имеет место, для сходственных моментов времени (для сходственных точек пространства) справедливо соотношение
 ,
,  .
.
Теперь поставим такую задачу: выполнить еще одну модель, подобную натуре, с тем же коэффициентом подобия
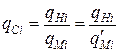 ,
, 
(штрихом помечаем величины, относящиеся ко второй модели). В таком случае все соответствующие критерии подобия второй модели и натуры будут равны (обеспечиваем при создании второй модели достаточные условия их подобия).
Кроме того, имеем:
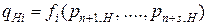 ,
,
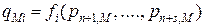 ,
, 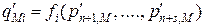 .
.
Но поскольку 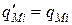 то, ввиду отмеченной однозначности,
то, ввиду отмеченной однозначности,
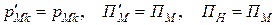 ,
,
т. е. в нашем случае, при подобии модели и натуры соответствующие критерии модели и натуры равны.
2. Если одному и тому же значению qi могут соответствовать различные наборы параметров pк, то в общем случае при подобии не все критерии модели и натуры равны. Например, если П 1 = sin П 2, то равенство П 1 М = П 1 Н возможно при
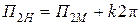 ,
, 
Отметим, что рассмотренный случай встречается сравнительно редко, но его все же следует иметь в виду.
Таким образом: Необходимым условием подобия двух систем является равенство соответствующих критериев подобия этих систем, составленных из обобщенных координат и параметров систем.
Если достаточные условия накладывают определенные ограничения на параметры систем, обусловливая этим их подобие, то необходимые условия позволяют установить связь между координатами и параметрами систем.
2.3. П – теорема
Теорема теории подобия, известная под названием П -теоремы, формулируется следующим образом: функциональная зависимость между характеризующими процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия.
Использование теоремы дает известные преимущества при экспериментальном исследовании. Применяя безразмерные комплексы величин, полученные результаты можно распространить на все подобные процессы и уменьшить число величин, которые следует связать функциональной зависимостью. Действительно, в этом случае вместо n+s величин имеем n+s– 3 безразмерных комплексов, и нахождение зависимости между ними упрощается. Особенно легко находится эта зависимость, если критериев всего два; тогда для определения вида функции П 1= f (П 2) достаточно сравнительно небольшого числа измерений.
Пусть, например, требуется исследовать движение математического маятника. Характеризующие маятник величины: период Т,длина нити l,ускорение свободного падения g,максимальный угол отклонения нити от вертикали j (в радианах). Из этих величин можно составить два безразмерных комплекса: j и 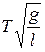 .
.
Следовательно  (j), откуда
(j), откуда 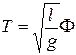 (j),
(j),
где Ф – некоторая функция максимального угла отклонения j.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Пример выполнения задания №1.
Задача 1. Груз массой т (рис. 1, а)колеблется на пружине жесткости С в вязкой среде, сила сопротивления Fk = – кu. На груз действует возмущающая сила F 0 sinwt. Перемещение груза х является функцией этих величин и времени:
x = f (m, k, w, F 0, с, t). (1)
 а)
а)
|  б)
б)
|  в)
в)
|
| Рис. 1 Колебания: а) колебания с демпфированием подвешенного к пружине груза; б) амплитудно-частотная характеристика в безразмерных координатах; в) электрический колебательный контур |
Решение 1:
Имеющиеся п величин р 1, р 2, р 3, …, рп,характеризующих процесс, дают п – r критериев подобия
П = с  …
… 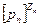 , (2)
, (2)
где r – ранг матрицы (3 – 4), 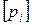 – размерность величины рi:
– размерность величины рi:
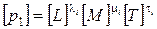 .
.
Числа z 1, z 2,..., zn таковы, что размерность П равна нулю. Величины z 1, z 2,..., zn находятся путем решения системы уравнений:
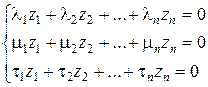 (3)
(3)
Система имеет п – r линейно независимых решений. Каждое решение, состоящее из п значений zi, дает один критерий подобия. Таким образом, необходимо решить систему (3). Степени размерностей  ,
, 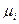 ,
,  для каждой величины указаны в таблице 1 (в данном случае p 1 = m, р 2 = с, p 3 = x, p 4 = t, p 5 =F 0, p6 = w, p 7 = k).
для каждой величины указаны в таблице 1 (в данном случае p 1 = m, р 2 = с, p 3 = x, p 4 = t, p 5 =F 0, p6 = w, p 7 = k).
Ранг матрицы, составленной на основе таблицы 1 равен трем.
Таблица 1.
| Величина | Степени | |||
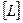
| 
| 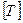
| ||
| p 1 р 2 p 3 p 4 p 5 p6 p 7 | m с x t F 0 w k | l 1 = 0 l 2 = 0 l 3 = 0 l 4 = 0 l 5 = 0 l 6 = 0 l 7 = 0 | m 1 = 1 m 2 = 1 m 3 = 0 m 4 = 0 m 5 = 1 m 6 = 0 m 7 = 1 | t 1 = 0 t 2 = – 2 t 3 = 0 t 4 = 1 t 5 = – 2 t 6 = – 1 t 7 = – 1 |
Система уравнений (3) примет вид
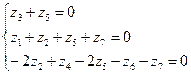 (4)
(4)
Число величин, характеризующих процесс, п = 7,ранг матрицы r = 3, поэтому система (4) имеет п – r = 4 линейно независимых решений. При нахождении этих решений; четыре величины zi (4 независимых решения!) имеют произвольные значения, остальные три величины находятся из (4). Это означает, что в (2) четыре значения zi выбираются произвольно, а остальные три такие, что критерий П является безразмерной величиной, т. е. остальные три значения «компенсируют» размерность, обусловленную выбором первых четырех величин. Произвол в выборе некоторых чисел z не имеет никакого значения, важно лишь одно – чтобы величина П была безразмерной. Поэтому выбираем наиболее простые значения, причем для тех z, для которых это возможно по уравнениям (4) – например, дать произвольные значения для z 1, z2, z 3, z 7 нельзя, поскольку в таком случае первое и второе уравнения системы (4) противоречат друг другу.
1. Принимаем
z 1 = 1, z 2 = z 6 = z 7 = 0
Тогда
z 3 + z 5 = 0, 1 + z 5 = 0, z 4 – 2 z 5 = 0
откуда
z 5 = – 1, z 3 = 1, z 4 = – 2
Итак, первое решение:
z 1 = 1, z 2 = 0, z 3 = 1, z 4 = – 2, z 5 = – 1, z 6 = 0, z 7 = 0.
2. Принимаем
z 1 = 0, z 2 = 1, z 6 = z 7 = 0.
Тогда из (4)
z 3 + z 5 = 0, 1 + z 5 = 0, – 2 + z 4 – 2 z 5 = 0,
откуда
z 5 = – 1, z 3 = 1, z 4 = 0.
Итак, второе решение:
z 1 = z 2 = 0, z 3 = 1, z 4 = 0, z 5 = – 1, z 6 = z 7 = 0.
3. Принимаем
z 1 = z 2 = 0, z 6 = 1, z 7 = 0.
Тогда из (4)
z 3 + z 5 = 0, z 5 = 0, z 4 – 2 z 5 – 1= 0,
откуда
z 5 = 0, z 3 = 0, z 4 = 1.
Следовательно, третье решение:
z 1 = z 2 = z 3 = 0, z 4 = 1, z 5 = 0, z 6 = 1, z 7 = 0.
4. Принимаем
z 1 = z 2 = z 6 = 0, z 7 = 1.
Тогда из (4)
z 3 + z 5 = 0, z 5 + 1 = 0, z 4 – 2 z 5 – 1 = 0,
откуда
z 5 = – 1, z 3 = 1, z 4 = – 1.
Поэтому четвертое решение:
z 1 = z 2 = 0, z 3 = 1, z 4 = – 1, z 5 = 1, z 6 = 0, z 7 = 1.
Таким образом, получено четыре решения, которым соответствуют четыре независимых критерия подобия.
Из первого решения получаем критерий
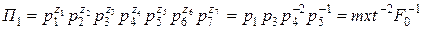 ,
,
 .
.
Из второго решения
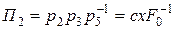 ,
, 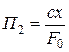
Из третьего решения
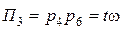 .
.
Из четвертого решения
 ,
, 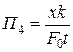 .
.
Решение 2:
Критерии подобия можно получить и несколько иным способом, используя ту же последовательность, которая применена для доказательства достаточного условия подобия (метод нулевых размерностей). Так, выбрав какие-либо три параметра (по числу первоначальных основных единиц – метр, килограмм, секунда), для которых определитель  , можно в соотношении (1) перейти к безразмерным величинам. Такими параметрами могут быть т, w, F 0,
, можно в соотношении (1) перейти к безразмерным величинам. Такими параметрами могут быть т, w, F 0,
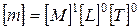 ,
, 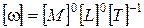 ,
,  .
.
Для них
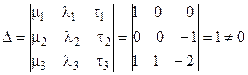 .
.
Уравнение (1) можно выразить так:
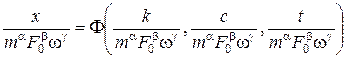 . (5)
. (5)
Значения 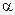 ,
, 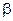 ,
, 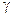 определяем из условия, что входящие в (5) комплексы – безразмерные величины:
определяем из условия, что входящие в (5) комплексы – безразмерные величины:
1) 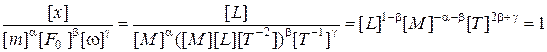
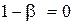 , откуда
, откуда  ;
;
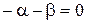 , откуда
, откуда 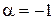
 , откуда
, откуда 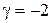 ,
,
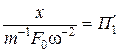 ,
, 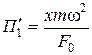 .
.
2) 
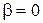 ;
; 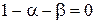 , откуда
, откуда 
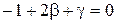 , откуда
, откуда 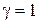 ,
,
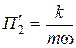 .
.
3) 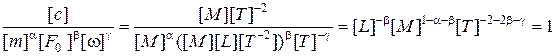
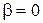 ;
;  ,
, 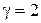 ,
, 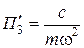 .
.
4) 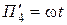 .
.
Из полученных результатов видно, что четыре критерия  соответствуют четырем критериям
соответствуют четырем критериям 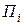 .
.
ЗАДАНИЕ №1
0. Найти критерии подобия и установить их взаимосвязь для случая истечения сыпучего материала из отверстия. Рассмотрим идеализированный случай, считая, что слипание частиц и внутреннее трение отсутствуют. Тогда параметрами процесса являются: Q – расход сыпучего материала, кг/сек; D – диаметр отверстия, м; d – средний размер зерна, м; r – плотность, кг/м3; g – ускорение свободного падения. Расход материала Q является функцией остальных параметров.
1. Найти критерии подобия и установить их взаимосвязь при определении силы сопротивления, действующую на тело заданной формы, движущееся с некоторой скоростью в вязкой тяжелой жидкости, имеющей свободную поверхность. Величину силы определяют следующие величины: v – скорость тела, м/сек; r – плотность жидкости, кг/м3; ν – кинематическая вязкость, м2/сек; l – некоторый характерный размер, м; g – ускорение свободного падения, м/сек2.
2. Найти критерии подобия и установить их взаимосвязь при определении силы сопротивления, действующую на тело заданной формы, движущееся с некоторой скоростью в вязкой тяжелой жидкости, имеющей свободную поверхность. Величину силы определяют следующие величины: v – скорость тела, м/сек; r – плотность жидкости, кг/м3; v – кинематическая вязкость, м2/сек; l – некоторый характерный размер, м; g – ускорение свободного падения, м/сек2:
3. Рабочий процесс вентилятора определяют следующие величины: плотность среды r, кг/м3, число оборотов в единицу времени п, 1/сек; диаметр винта D, м; расход воздуха Q, мг/сек; напор Н, н/м2 и мощность N, вт. Определить критерии подобия.
4. Рабочий процесс поршневой машины определяется следующими величинами: мощность, N, Вт, среднее давление газа, pср, МПа; l – длина хода; D, м – диаметр; n – число оборотов вала кривошипа в минуту. Определить критерии подобия.
5. Жидкость, которую можно считать несжимаемой, истекает из круглого отверстия радиусом r, м в среду с давлением P, МПа. Коэффициент расхода μ. Давление полного торможения в среде, из которой истекает жидкость равно P*, МПа. Определить критерии подобия.
6. Определить напряжения во вращающемся диске постоянной толщины. Наружный радиус диска, r1, м; радиус отверстия, r2, м; коэффициент Пуассона, μ; удельный вес, g; ускорение свободного падения, g; число оборотов, n; расстояние от центра до точки, где определяется напряжение, l; компоненты напряжений σr и σt.
7. Определить силу сопротивления действующую на тело заданной формы, движущееся с некоторой скоростью в вязкой тяжелой жидкости, имеющей свободную поверхность. При движении происходит обмен теплом между телом и жидкостью. Скорость тела u, м/с; плотность жидкости r, кг/м3; кинематическая вязкость n, м2/с; характерный размер l, м; ускорение свободного падения g, м/сек2; количество теплоты Q, Дж; теплоемкость жидкости с, Дж/ кг×К; температура жидкости T, К.
8. Рабочий процесс вентилятора авиационного двигателя определяют следующие величины: плотность среды r, кг/м3, число оборотов в единицу времени п, 1/сек; диаметр миделевого сечения D, м; расход воздуха G, мг/сек; давление за вентилятором p, н/м2; мощность N, Вт; высота полета H, м; скорость полета u, м/с; температура окружающей среды на заданной высоте T, К.Определить критерии подобия.
9. Рабочий процесс свободной турбины ГТУ определяют следующие величины: плотность среды r, кг/м3, число оборотов в единицу времени п, 1/сек; диаметр D, м; расход продуктов сгорания G, мг/сек; давление за свободной турбиной p, н/м2; мощность N, Вт; температура продуктов сгорания на входе в турбину T, К; сила тока на генераторе I, А. Определить критерии подобия.
Пример выполнения задания №2.
Задача 1. Необходимо опытным путем определить распределение температур в длинном стальном вале диаметром d = 400 мм через τ = 2,5 ч после загрузки его в печь.
Для стали коэффициенты теплопроводности и температуропроводности равны соответственно λ =42 Вт/(м°С), a =1,18× 10-5 м2/с. Коэффициент теплоотдачи к валу в печи α = 116 Вт/(м2×°С).
Исследование решено проводить в небольшой печи на геометрически подобной модели вала, выполненной из легированной стали. Для модели λ м = 16 Вт/(м°С); ам = 0,53×10-5 м2/с;α м = 150 Вт/(м2×°С);
Определять диаметр dм модели вала и промежуток времени, через который после загрузки модели в печь необходимо измерить распределение температур в модели,
Решение:
Подобие температурных полей вала и модели будет иметь место при равенстве критериев для образца и модели:
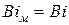 и
и  .
.
Критерии Био и Фурье для вала
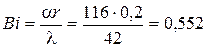 ;
;
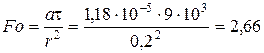 .
.
Из условия 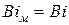 находим диаметр модели вала:
находим диаметр модели вала:
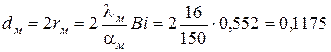 м.
м.
Из условия  находим искомый промежуток времени:
находим искомый промежуток времени:
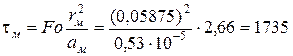 с.
с.
Задача 2. На паропроводе перегретого пара диаметром d =400 мм установлена измерительная диафрагма, которая должна быть специально протарирована, т. е. должна быть найдена зависимость Δ р =f (G),где Δ р – перепад статических давлений в диафрагме, Па; G – расход пара, кг/с.
Так как по производственным причинам тарировка не могла быть произведена непосредственно на образце, то для этой цели была изготовлена модель в 1/5 натуральной величины.
В результате испытаний модели на воде, температура которой t ж м = 20°С, были получены значения перепадов давлений на диафрагме при различных расходах воды. Результаты измерений приведены ниже:
| Δ р, Па | 18 050 | 72 200 | |||
| G, кг/с | 2,22 | 4,44 | 8,88 | 17,76 | 35,52 |
Найти зависимость Δ р =f (G) для образца при течении пара в автомодельной области и указать границы ее применения. Давление пара р =98 кПа. Температура пара t ж=250°С.
Решение:
Произведем обработку опытных данных в критериях подобия и построим зависимость Eu =f (Re). Эта зависимость будет действительна и для пара. Поэтому по полученной для модели зависимости Eu =f (Re) можно найти зависимость Δ р =f (G)для случая течения пара в образце.
Для определения зависимости Eu =f (Re) подсчит