ЛАБОРАТОРНАЯ РАБОТА № 1.
В начале рассмотрим идею метода Монте – Карло. Пусть у нас есть какая – нибудь фигура на плоскости, площадь которой (Sfig ) нам необходимо найти. Ограничим ее другой фигурой, площадь которой (Stotal) мы можем легко вычислить. Например, прямоугольником АСDB со сторонами, параллельными координатным осям (см. рис. 1). И пусть про любую точку прямоугольника мы можем быстро узнать, попадает эта точка внутрь фигуры, площадь которой мы ищем, или нет.

А теперь начнем опыт – будем бросать на бумагу зерна случайным образом (вообще – то это нелегко сделать, чтобы обеспечить случайность). Когда нам покажется, что зерна почти полностью покрыли бумагу, посчитаем, сколько всего зерен на прямоугольнике (пусть их число Ntotal) и сколько из них на фигуре (Nfig). Ясно, что число зерен, попавших внутрь фигуры, пропорционально ее площади: больше площадь – больше зерен, меньше площадь – меньше зерен. Поэтому, поделив количество зерен, попавших внутрь фигуры, на количество всех зерен в прямоугольнике, мы сможем найти, какую часть площади прямоугольника занимает фигура:
Nfig / Ntotal  Sfig / Stotal, отсюда Sfig
Sfig / Stotal, отсюда Sfig  Nfig / Ntotal * Stotal
Nfig / Ntotal * Stotal
Промоделируем этот опыт на ЭВМ. Предположим, нам надо найти площадь фигуры ограниченной сверху кривой Y = F(X), а снизу – осью абсцисс. Пусть Y = cos(X), а Х I [– p /2, p /2] (см. рис. 2). Ограничим нашу фигуру прямоугольником АСDB, его площадь равна p.
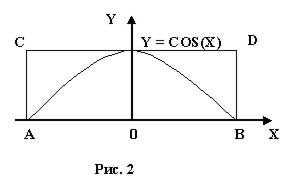
Из чего должен состоять алгоритм:
1. Бросание зерна – бросание случайной точки, координаты X и Y которой случайны, причем Х должна меняться от – p /2 до p /2, а Y – от 0 до 1. И в этих интервалах X и Y должны появляться с одинаковой вероятностью в любой точке этих отрезков, т.е. X и Y должны быть равномерно распределены по осям. Тут надо напомнить ребятам, как получить равномерно распределенное случайное вещественное число на интервале [А, В]:
Х = random* (B – A) + A
2. Надо определить, куда попала точка – под кривую или выше нее. И вести подсчет Nfig. Условие попадания точки под кривую: Y? sin (X).
3. Повторить пп.1 и 2 столько раз, чтобы получить желаемую точность результатов.
Дети без труда напишут программу по данному алгоритму (на практическом занятии). И после этого наступает момент разочарования. Сухие цифры...
Предложение учителя: давайте создадим проект в Delphi, который наглядно демонстрировал бы работу метода Монте – Карло. Разработаем интерфейс программы. Тут ребята сами предлагают несколько вариантов оформления проекта, один из которых представлен на рис. 3.
Разместим на форме следующие компоненты:
Edit – окно редактирования для ввода общего количества испытаний (бросков зерен) – Ntotal;
Button – кнопка для запуска работы метода Монте – Карло;
Panel – панель для вывода посчитанной площади фигуры;
(все вышеперечисленные компоненты расположены на вкладке Standart Палитры компонентов)
Image – для вывода точек, попавших в искомую область (компонент расположен на вкладке Additional Палитры компонентов).
Если необходимо, надо напомнить ребятам некоторые свойства и методы выбранных компонентов (это может быть и домашним заданием предыдущего урока, чтобы не терять время на “воспоминания”).
Компонент Edit:
Свойство Text – содержит текст, который пользователь набирает в окне Edit. Этот текст надо преобразовать в число Ntotal. Для этого в Delphi есть необходимая функция StrToInt:
Ntotal = StrToInt (Edit1.Text).
Компонент Panel:
Свойство Caption – содержит текст, который выводится на панель. Чтобы вывести полученное число Sfig на панель, мы должны преобразовать его в строку S с помощью процедуры Str:
Str(Sfig:10:4, S),
а потом вывести эту строку на панель следующим образом:
Panel1.Caption:= ‘Площадь фигуры = ‘ + S
Компонент Image:
Свойства Height и Width – соответственно высота и ширина компонента;
Свойство Canvas – отводит канву (место) для рисования на компоненте Image;
Методы Canvas:
FillRect(ClientRect) – закрашивает область клиента компонента Image каким – либо цветом
(по – умолчанию – белым), т.е. стирает предыдущую картинку;
MoveTo(X, Y) – перемещает перо в точку с координатами X, Y без проведения линии (координаты задаются в пикселях);
LineTo(X, Y) – проводит линию из текущей точки в точку с координатами X, Y;
Pixels[I, J] – содержит цвет точки с координатами I, J.
У кнопки (компонент Button) мы будем обрабатывать событие onClick (событие нажатие кнопки). Т.е. вышеописанный алгоритм мы программируем в процедуре Button1Click.
Тут учитель задает вопрос классу: “ Какая проблема возникает при выводе точки на экран (на компонент Image)?” Ответ: расчетные координаты очень малы (0? Y? 1,меньше пикселя, -p /2? X? p /2); а если взять другую кривую Y = F(X), они могут оказаться слишком большими (больше размера компонента Image). Поэтому, при выводе значений функций (графиков) на экран монитора, необходимо преобразовывать расчетные координаты в графические с учетом дискретности растровой сетки монитора, а также предусмотреть возможность автоматического масштабирования функции (графика) по осям координат. Для этого желательно создать отдельную подпрограмму.
Для полного размещения функции (графика) в расчетной области (это область компонента Image) необходимо определить X_min, X_max, Y_min, Y_max – минимальные и максимальные значения по X и по Y соответственно. X_min =А, X_max = В. Как найти Y_min, Y_max.
Коллективно обсуждается следующий алгоритм:
1. Разобьем интервал [А, В] по Х на N равных частей и определим массивы значений аргумента и функции X[i] и Y[i] = F(X[i]), где I = 1..N;
2. Определяем наибольшее Y_max и наименьшее Y_min значения функции в заданном интервале изменения аргумента;
3. Находим коэффициенты масштабирования Kx, Ky при построении графика в заданной области;
4. Т.к. коэффициенты масштабирования Kx, Ky могут отличаться, то выводимый график может искажаться. Устраняем искажения графика;
5. Преобразуем расчетные координаты точки X, Y в графические Xg, Yg. С учетом того, необходимости “переворота” оси Y, которая в координатах монитора направлена сверху вниз.
Листинг программы, реализующей данные алгоритмы представлен в конце статьи. Результат работы программы при разном количестве испытаний представлен на рис. 3, 4.


Задания для самостоятельной работы:
1. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, p ];
2. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = cos (X), при Х I [ -p, 0 ];
3. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, 2p ];
4. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = cos (X), при Х I [ -p, p ];
5. Доработать проект:
а) организавать проверку правильности ввода информации в поле Edit (чтобы вводились только целые числа);
б) разметить оси и подписать числовые значения.
На последующих уроках, на которых предполагается изучение тем “Вычисление площадей (интегралов) методом трапеций и методом прямоугольников”, можно предложить ребятам доработать проект, поместив на форму дополнительные компоненты Image, Button, Edit, Panel (для каждого численного метода – свои). В окно компонента Edit пользователь будет вводить количество разбиений интервала [А, В] по Х. Таким образом, ребята смогут сравнить и наглядно увидеть работу всех трех численных методов.
Листинг программы
unit Monte;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, Buttons;
type
TForm1 = class(TForm)
Panel1: TPanel;
BitBtn1: TBitBtn;
Edit1: TEdit;
Label1: TLabel;
Image1: TImage;
procedure BitBtn1Click(Sender: TObject);
private
{Private declarations }
public
{Public declarations}
end;
const A = -Pi/2.0; B = pi/2.0; n = 1000;
var
Form1: TForm1;
N_total:longint;
implementation
{$R *.dfm}
Function FUNC(x:real):real;
begin
Func:=Cos(x);
end;
Procedure Graphic(var right, down: integer;
var X_min, X_max, Y_min, Y_max, Kx, Ky: real);
type arr=array[1..n] of real;
var
X, Y: arr; dx: real;
i: integer;
begin
dx:=(B-A)/(n-1);
for i:=1 to n do begin X[i]:=A+dx*(i-1);
Y[i]:=FUNC(X[i]);
end;
{Нахождение максимального и минимального значений функции и аргумента}
X_max:=B; X_min:=A;
Y_max:=Y[1]; Y_min:=Y[1];
for i:=2 to n do begin
if Y_max < Y[i] then Y_max:=Y[i];
if Y_min > Y[i] then Y_min:=Y[i];
end;
{Нахождение коэффициентов сжатия}
Kx:=right/(X_max-X_min);
Ky:=down/(Y_max-Y_min);
{Устранение искажения графика}
if Kx < Ky then begin
Ky:=Kx;
down:=round((Y_max-Y_min)*Ky);
end
else begin
Kx:=Ky;
right:=round((X_max-X_min)*Kx);
end;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var N_total, N_fig, i:longint;
S_total,S_fig,X,Y:real;
Xg, Yg: integer;
X_min, X_max, Y_min, Y_max, Kx, Ky: real;
Right, Down: integer;
S:string;
begin
randomize;
With Image1, Canvas do
begin
FillRect(ClientRect);
Right:= Width;
Down:= Height;
Graphic(Right, Down, X_min, X_max, Y_min, Y_max, Kx, Ky);
Width:= Right;
Height:= Down;
{Рисование осей}
Xg:=round(-X_min*Kx);
Yg:=Down-round(-Y_min*Ky);
{Ось Y}
MoveTo(Xg,Down);
LineTo(Xg, 0);
moveto(Xg, 0);
lineto(Xg+4, 10);
moveto(Xg, 0);
lineto(Xg-4, 10);
{Ось Х}
MoveTo(0, Yg-1);
lineTo(Right, Yg-1);
moveto(Right, Yg);
lineto(Right-10, Yg+5);
moveto(Right, Yg);
lineto(Right-10, Yg-5);
N_fig:=0;
N_total:=StrToInt(Edit1.Text);
{Розыгрыш координат точек}
for i:=1 to N_total do
begin
X:=random*(B-A)+A;
Y:=random*(Y_max-Y_min)+Y_min;
if Y <= FUNC(X)then
begin
Xg:=round((X-X_min)*Kx);
Yg:=Down-round((Y-Y_min)*Ky);
Pixels[Xg, Yg]:=clBlack;
Application.ProcessMessages;
N_fig:=N_fig+1;
end;
end;
end;
S_fig:=(Y_max-Y_min)*(B-A)*N_fig/N_total;
Str(S_fig:10:4,S);
Panel1.Caption:='Площадь фигуры = '+S;
end;
end.
Литература
1. Флеонов М.Е. Библия Delphi. – 3-е изд., перераб. и доп. – СПб.: БХВ-Петербург, 2011. – 688 с.
2. Солодовников А.С. Теория вероятностей: Учеб. Пособие для студентов пед. ин-тов по матем. спец. – М.: Просвещение, 1983. – 207 с.
3. Андрухаев Х.М. Сборник задач по теории вероятностей: Учеб. Пособие для студентов пед. ин-тов по спец. 2104 «Математика», «Математика с доп. спец. физика» и 2105 «Физика с доп. спец. математика» / Под ред. А.С. Солодовникова.—М.: Просвещение, 1985. – 160 с.
4. Виленкин Н.Я., Потапов В.Г. Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистики. – М.: Просвещение, 1979. – 112 с.
5. В.Е. Гмурман Теория вероятностей и математическая статистика. Изд. 7, - М. «Высшая школа» 2002.