ИЗУЧЕНИЕ РЕЗОНАНСА НАПРЯЖЕНИЯ И ТОКА В

ПОСЛЕДОВАТЕЛЬНОМ И ПАРАЛЛЕЛЬНОМ

КОЛЕБАТЕЛЬНЫХ КОНТУРАХ

1.Цель работы: теоретически изучить методы расчёта электрической цепей при периодических (синусоидальных) токах и напряжениях.

Экспериментально исследовать вынужденные колебания в последовательном и параллельном электрических контурах.

 

2. Теоретическая часть

Переменным током называется ток, меняющийся как по амплитуде (величине) так и направлению.

При расчёте электрических цепей для квазистационарных токов справедливы законы Ома и Кирхгофа. Но в случае берутся мгновенные значения изменяющихся токов и напряжений. Квазистационарными называются токи, для которых их мгновенные значения во всех сечениях цепи одинаковы. Математически условие квазистационарности имеет вид:

<< Т,

где τ – время необходимое для передачи электрического возмущения в самую отдаленную точку цепи;ℓ – длина цепи; с – скорость света; Т – период колебания.

В расчётах электрических цепей при решении практических задач для переменного тока всё сводится к нахождению амплитудных и мгновенных значений тока и напряжения, сдвига фаз между током и напряжением, и полного и реактивного сопротивления цепи.

Рассмотрим простейшие электрические цепи.

1. Цепь, состоящая из активного сопротивления

К активному сопротивлению приложено напряжение, изменяющееся по закону U =U_m cos ωt

 

Рис.1

Для мгновенных значений тока и напряжения справедлив закон Ома, то

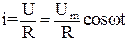
Соотношение 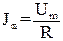представляет собой закон Ома для амплитудных значений. Соотношение между переменными токами и напряжениями делаются особенно наглядными, если изображать их с помощью векторов.

Выберем произвольное направление, которое назовем осью токов (Рис.1). Отложим вдоль этого направления вектор напряжения. Поскольку напряжение и ток в рассматриваемом случае изменяются синфазно, вектор напряжения также будет направлен вдоль оси токов: длина его равна RJ. Совокупность векторов напряжений или токов образует векторную диаграмму данной цепи.

Рис.2

2. Цепь, состоящая из индуктивности

Подадим переменное напряжение на концы индуктивности L, тогда в ней начнет течь ток, вследствие чего возникает ЭДС самоиндукции. По закону самоиндукции . При условии равенства нулю активного сопротивления индуктивности, чтобы ток в цепи не был бесконечно большим, должно выполняться условие ε_u = - U. Поэтому 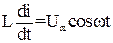. Перепишем уравнение в виде di = 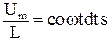Интегрирование этого уравнения дает:

i = 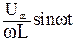или i = ,

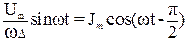где J_m = - закон Ома для амплитудных значений тока и напряжения.

Сопоставляя соотношения закона Ома, мы видим, что роль сопротивления в данном случае играет величина x_L= ω L, которую называют реактивным сопротивлением L. Из сравнения выражений тока и напряжения следует, что падение напряжения из индуктивности опережает, а по фазе ток, текущий по ней на 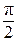. Если направить ось токов по горизонтали, то получится векторная диаграмма (рис.2).

3. Цепь, состоящая из ёмкости

Пусть напряжение подано на ёмкость С (рис.3). Ёмкость непрерывно перезаряжается, вследствие чего в цепи течёт переменный ток.

Поскольку сопротивление подводящих проводов пренебрежимо мало, напряжение на конденсаторе U_c = можно считать равным внешнему напряжению U U_c = = U_m cos ωt

Производная от q до t даст силу тока в цепи i. Умножим выражение напряжения на С и, продифференцировав по t, заменив q на I, получим

i = -ωCU_msinωt = J_m cos(ωt + 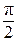), где J_m = ωCU_m = . Величина x_c = называется реактивным ёмкостным сопротивлением. Падение напряжения на ёмкости U_c = 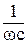cos ωt. Сравнивая это напряжение с выражением для тока находим, что падение напряжения на ёмкости отстает по фазе от текущего через ёмкость тока на 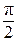. (рис.4). Причина отставания заключена в том, что до тех пор, пока ток течёт в одном и том же направлении, заряд на обкладках конденсатора растёт. Сила тока проходит через макcимум и начинает убывать, а заряд(а следовательно и U_c) всё ещё продолжает расти, достигая макcимума в тот момент, когда i обращается в нуль.

Рис.3 Рис.4

4. Цепь, состоящая из последовательно соединенных сопротивлений,

индуктивности и ёмкости. Резонанс напряжения

а) Рассмотрим цепь, составленную из включённых последовательно элементов R, L,C. Подадим на концы этой цепи напряжение U =U_m cos ωt. В цепи возникает переменный ток амплитуда и фаза которого, очевидно, определяются параметрами цепи R, L, C (рис.5).

В цепях постоянного тока напряжение на концах цепи амплитуды напряжений на отдельных, последовательно соединенных участках поля

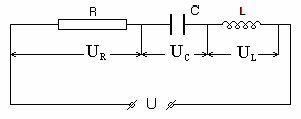
Рис.5

Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.

Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга. Действительно, ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с ёмкостным, индуктивным и активным сопротивлениями. Однако только на активном сопротивлении колебания напряжения и тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний тока на 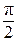, а на катушке индуктивности колебания напряжения опережают колебания тока на .

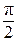Проще всего выполнить сложение нескольких гармонических колебаний с помощью метода векторных диаграмм. Идея метода основана на двух довольно простых положениях.

Во-первых, как известно, проекция вектора с модулем х_м,1, вращающегося с постоянной угловой скоростью, совершает гармонические колебания:

х₁=х_м,1соs ωt х₁ = х₁соs ωt

Во-вторых, при сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.

Пусть складываются два гармонических колебания одинаковой частоты, но различающиеся по амплитуде и фазе. Второе колебание сдвинуто по фазе относительно первого на φ₀ и определяется формулой:

х₂ = х_м,2 соs (ωt + φ₀) х₂= х₂ соs (ωt + φ₀)

Каждое из этих колебаний можно рассматривать как проекцию соответствующего вектора, вращающегося со скоростью ω, причем второй вектор образует с первым угол φ (рис.6). Суммарное смешение х, равное сумме смещений

х₁ и х₂: х =х_м,1соs ωt + х_м,2 соs (ωt + φ₀),

согласно второму положению, представляет собой проекцию суммарного вектора, вращающегося со скоростью ω х = х_м соs (ωt + φ), где х_м -модуль суммарного вектора, а φ -угол между этим вектором и вектором, проекция которого равна х₁. Этот угол определяет сдвиг фазы результирующего колебания относительно колебания х₁.

Итак, графическое изображение гармонических колебаний и соотношений между гармонически колеблющимися величинами с помощью векторов называется векторной диаграммой.

В последовательном колебательном контуре падение напряжения на активном сопротивлении U_R, амплитуда которого равна RJ_м, а фаза совпадают с фазой тока. Поэтому на векторной диаграмме вектор, изображающий U_R, нужно отложить по оси токов. Падение напряжения на индуктивности U_L с амплитудой ωLJ_m опережает ток по фазе на 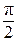, поэтому вектор, изображающий U_L, должен быть повернут относительности токов на угол 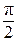против часовой стрелки. Наконец, падение напряжения на ёмкости U_C, имеющее амплитуду 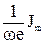отстает от тока по фазе на 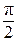, следовательно, вектор, изображающий U_c, должен быть повернут относительно оси токов на угол 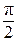по часовой стрелке.

 

Рис.6

Падение напряжений U_R,U_L, U_c в сумме должны быть равны приложенному к цепи напряжению U. Поэтому, отложив векторы, изображающие U_R,U_L, U_c, мы получим вектор, изображающий U. Его длина равна Uм. Этот вектор образует с осью токов угол φ, который, как видно из рис.6, равен .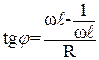

Угол φ дает разность фаз между напряжением U и прямоугольного треугольника, гипотенуза которого U_m. По теореме Пифагора, следует,

что (RJ_m)² + [(ωL – 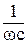) J_m]² =U_m.

Откуда J_m = .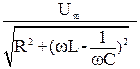

(Закон Ома для амплитудных значений переменного тока)

Величина Z =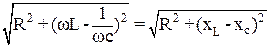

называется полным сопротивлением цепи. А величина Х = Х∆ -Х_с =ωL – 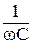называется реактивным сопротивлением. Таким образом 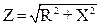. Ток отстает от напряжения (φ > 0) или опережает его (φ < 0) в зависимости от соотношения между x_L x_e. При ωL> 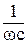ток отстает от напряжения. Если ωL = 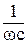изменение тока и напряжения происходит синфазно (φ=o). При удовлетворяющей этому условию частоте 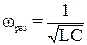полное сопротивление имеет наименьшее значение, равное К. Соответственно сила тока достигает наибольшего значения. При этом падение напряжения при активном сопротивлении равно внешнему напряжению, приложенному к цепи. Падения напряжения на ёмкости U_c и индуктивности U_L одинаковы по амплитуде и противоположны по фазе. Это называется резонансом напряжений. 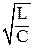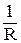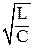Значение резонансной частоты мoжет быть получено из условия U_L =U_c,раз = J_м = U_м.

Если > R, напряжение на индуктивности и на ёмкости превышает напряжение, приложенное к цепи.

Явление резонанса напряжений характерно тем, что полное сопротивление цепи оказывается чисто активным (т.е и напряжение изменяются синфазно) и имеет наименьшую возможную при данных параметрах цепи величину.

Расчёты цепей переменного тока значительно упрощаются, если применять так называемый символический метод. Он основывается на том, что, как известно из курса математики, каждому вектору A, расположенному в координальной плоскости, можно сопоставить комплексное число Â = а =вj =Aℓ^jα, где a и в -проекция вектора на А-модель комплексного числа λ- аргумент комплексного числа j - мнимая единица ()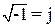

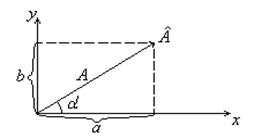
Рис.7

Применение символического метода для расчёта электрических цепей переменного тока предполагает знание основ свойств комплексных числах (проработать данные приложения).

Так как комплексные числа геометрически представляются векторами на плоскости, то все векторные физические величины могут быть охарактеризованы при помощи комплексных чисел. Представление векторных физических величин комплексными числами облегчает выполнение расчётов этих величин, так как действия над векторами, которые выполняются графически, заменяются соответствующими действиями над комплексными числами, которые выполняются аналитически, что значительно проще. При этом комплексные числа могут быть взяты в алгебраической, тригонометрической или показательной формах в зависимости от конкретного случая, а + jв = (соs φ +j sin φ) z = Aℓ^jφ

В частности, переменное напряжение дается уравнением

U = U_м cosωt

При стандартной частоте 50 Гц угловая частота ω является постоянным числом = 314рад/с, следовательно, в этом случае уравнение напряжения полностью определяется двум параметрами – амплитудой U_м и φ и начальной фазой. Аналогичная ситуации имеет место для уравнений тока и электродвижущей силы:

i = J_м Sin (ωt + φ), е = ε_мsin (ωt + φ)

Тот факт, что при фиксированной частоте уравнение напряжения определяется двумя параметрами U и φ, позволяет сопоставить каждому такому уравнению комплексное число U_м (соs φ + sin φ), модуль

Û= U_м(соs φ + sin φ)

При этом комплексное число Û называется комплексным напряжением. Сумма двух и более гармонических колебаний с одной и той же угловой частотой ω является также гармоническим колебанием с той же угловой частотой ω, которому соответствует комплексное число Û, равное сумме комплексных чисел Û₁ Û ₂ (соответствующих величинам U₁ U₂).

Между величинами а и в, A и α имеются следующие соотношения:

A =

При сложении комплексных чисел складывается отдельно их вещественные и мнимые части:

 =∑Â_к =∑а_к + ј∑в_к

Легко видеть, что соответствует сумме векторов, изображаемых комплексными числами Â_к (рис.8).

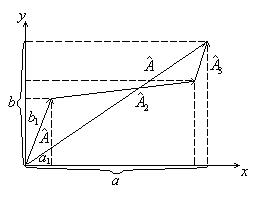
Рис.8

Из правила перемножения двух комплексных чисел А·е^јα·Ве^јβ=АВе^јωt вытекает, что умножение комплексной величины Â= Ае^јα, изображающей вектор А, на комплексное число е^јφ равнозначно повороту вектора А на угол φ против часовой стрелки. Если φ= 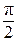, то е^јφ =соs 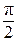+ sin 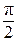=ј. Таким образом, умножение на ј равнозначно повороту вектора на угол 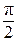по часовой стрелке. Аналогично умножение на = - ј равнозначно повороту вектора на угол 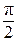по часовой стрелке.

Произведем с помощью символического метода вычисление падения напряжений на индуктивности и ёмкости Û_L =L 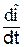. Если через индуктивность течет ток î = J_ме^јωt, то

Û_L = L 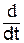(J_м е^јωt) = јωL J_ме^јωt =јωL î.

Таким образом, для того чтобы получить вектор напряжения U_L, нужно вектор силы тока умножить на ωL и повернуть против часовой стрелки на угол 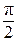. Этот результат полностью совпадает с результатом нахождения U_L выше. U_С = 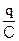. Заряд на конденсаторе q =Sidt. Подставляя это выражение в формулу для U_С и перейдя на символическую запись, получим

Û_с = 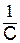Sîdt.

После подстановки значения тока Û_с= 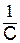SJ_ме^јωt·dt = 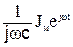= - î.

Падение напряжения на активном сопротивлении, очевидно, равно Û_R=Rî.

Для последовательного колебательного контура, то есть последовательно включенных R,C,L U = UR + Û_L + Û_с,, внешнее напряжение принимает вид

Rî+jωLî - î =Û, вынеся î за скобку, получим Û=î

(т.к. 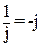) - величина 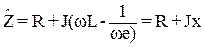называется комплексным сопротивлением. Его модуль равен полному сопротивлению, а аргумент φ равен сдвигу фаз между напряжением и током. Следовательно,

.

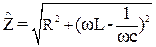
Используя комплексную форму записи закона Ома, можно получить Û=î =îZe^јα. Таким образом вектор напряжения Û можно получить, умножив вектор силы тока î на Z и повернув против часовой стрелки на угол φ (рис.8) Отдельные участки последовательной цепи, характеризуются комплексными сопротивлениями _k.

Сумма всех Û_k должна быть равна напряжению Û, приложенному к цепи

Û =Û_R + Û_c + Û_L Û= Σî _k = îΣ _k =î .

Таким образом, комплексное сопротивление последовательной цепи равно сумме комплексных сопротивлений её участков: = Σ _k

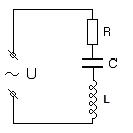
Рис.9

При параллельном соединении элементов цепи (параллельный колебательный контур) î = 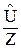, а ток равен сумме токов î_k, текущих по отдельным элементам цепи и определяемых выражением î_k = 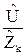. Поэтому î = .

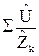Отсюда , или

5. Цепь, состоящая из параллельно соединенных индуктивности и ёмкости

(Резонанс токов).

Рассмотрим цепь, образованную включенными параллельно индуктивностью и ёмкостью (рис.10) В этом случае ì = јωÛ ì = 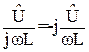(Û_с= Û_∆ = Û)

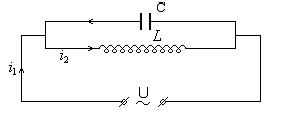
Рис.10

Из этих выражений можно видеть, что токи i₁ и i₂ находятся в противофазе. Ток в проводящих проводах i равен сумме токов i₁ и i₂ î = î₁+ î₂ =j(ωc- 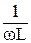)Û.

При условии, что ωc - 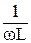= 0. Ток в проходящих проводах будет отсутствовать, хотя токи î₁ и î₂ в отдельных цепях могут быть очень велики. Это явление называется резонансом токов. Для резонансной частоты условие ωc - 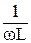=0 получается такое же значение как и при резонансе напряжений.

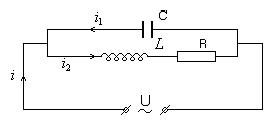
Соотношение между токами î₁ и î₂ можно изобразить с помощью векторной диаграммы. Но при построении диаграммы токов вектора î₁ нужно откладывать относительно оси напряжений, а не токов. Выберем в качестве этой оси – ось Х (рис.11)

Х

Рис.11 Рис.12

При резонансе длины векторов обоих токов одинаковы, результирующий ток равен нулю.

Практически индуктивность всегда обладает сопротивлением R. Это активное сопротивление и самоиндуктивность изображают раздельно (рис.12). Следовательно, отставание тока от напряжения будет меньше 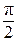. Оно определяется формулой tgφ= . В этом случае векторы î₁ и î₂ не коллиниадно исум-ма их не может быть равной нулю.

Комплексные сопротивления обоих ветвей равны .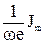

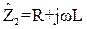Сопротивление всей цепи будем вычислять по формуле

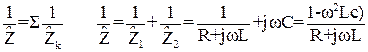
откуда

Умножив числитель и знаменатель на величину, комплексно сопряженную знаменателю, получим (т.е (1-ω²Lc) - jωcR

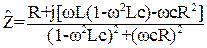
Модуль даст полное сопротивление параллельной цепи, а отношение реактивной и активной составляющих - тангенс угла φ, определяющего сдвиг фаз между напряжением и током (рис. 12).Можно показать, что максимум полного сопротивления (т.е. резонанс токов) достигается при условии, что реактивная составляющая обращается в нуль, и следовательно, полное сопротивление становится чисто активным (рис.12). Резонансную частоту можно найти, приравняв нулю мнимую часть выражения

ωL(1 – ω²Lc) –ωcR² = 0,

отсюда ω_раз = ,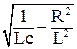

tgφ= .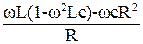

Зависимость тока от частоты и параллельном колебательном контуре может быть изображена графически (рис.).

Расчёт ω_раз можно представить так:

ωL-ω³L²C –ωCR² =0 L –ω² L² C –CR² =0 ω²L²C = L –CR²

Добротность колебательного контура

При резонансной частоте 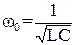индуктивное и ёмкостное сопротивление равны ω₀L =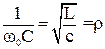

Величина ρ называется характеристическим сопротивлением контура. Отношение напряжения на индуктивности или ёмкости к напряжению, приложенному к цепи при резонансе, называется добротностью колебательного контура.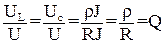

Добротность контура указывает, во сколько раз напряжение на индуктивности или ёмкости больше напряжения, приложенного к цепи.

При малом активном сопротивлении контура добротность можно вычислить по формуле Q = ∆ω берется на уровне 0,5 от U_max

3. Экспериментальная часть

ОПИСАНИЕ УСТАНОВКИ

Блок- схема установки Рис.13

1– генератор звуковой частоты; (ГЗ-3)

2– колебательный контур (последовательный или параллельный):

3– ламповый вольтметр (В7-15) или осциллограф

Порядок проведения эксперимента

При изменении частоты колебаний, подаваемых со звукового генератора, произвести измерения напряжений на элементах электрической цепи.

Предварительно выбрать диапазон изменения частоты генератора таким образом, чтобы напряжение на элементах колебательного контура U_L, U_C, U_LC, U_K. изменялось от максимума (~10В) до 0,5 В. Затем снять кривые зависимости напряжения от частоты в найденном диапазоне. Число измерений должно быть порядка 7—10 для U_L,U_c, и 12-15 для U_L,C и U_k-.

ЗАДАНИЕ 1. Исследование вынужденных колебаний в последовательном контуре (R,L,C) (резонанс напряжения).

ПРИНЦИПИАЛЬНАЯ ЭЛЕКТРИЧЕСКАЯ СХЕМА

1. Снять зависимость U_L f(ω), U_c = f(ω), U_∆,c = f(ω)

2. Построить экспериментальные и теоретические(расчётные) графики зависимости U_L, U_c, U_L,c, от частоты. Частоту колебаний звукового генератора следует изменить от 0 до 200 кГц,

Результаты измерений занести в таблицу1

Таблица 1

f,Гц
UL В
UC В
ULC В

 

ЗАДАНИЕ 2.Исследование вынужденных колебаний в параллельном колебательном контуре (резонанс токов.)

ПРИНЦИПИАЛЬНАЯ ЭЛЕКТРИЧЕСКАЯ СХЕМА

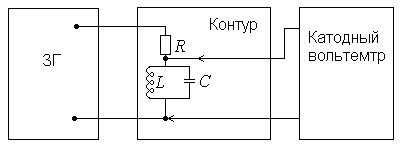
1.Снять зависимость U_k = f (ω)

Построить экспериментальные и теоретические (расчётные) графики зависимости напряжения на колебательном контуре от частоты. Изменение частоты генератора звуковых колебаний изменить от 0 до 200кГц с интервалом….

Результаты занести в таблицу 2

Таблица 2

f,Гц
UК В

 

2. По графику, построенному на основании данных эксперимента, найти добротность контура пол формуле Q =

∆ω - берется на высоте 0,5 амплитудного значения U_k

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Цель и производство работы

2. Резонанс напряжения и тока в последовательном и параллельном колебательном контурах.

3. Вывод формул для полного сопротивления, тока и сдвига фаз между током и напряжением в цепях содержащим R,C, L элементы при переменном токе

 

Работа № 13