МАТЕМАТИЧЕСКИЙ АНАЛИЗ
РЯДЫ
Учебно-методическое пособие
Краснодар
УДК 517
ББК 22.12
С13
В учебно-методическом пособии использованы материалы, разработанные доцентом кафедры «Информатика и ЭММ» Миселимян Т.Л.
Рецензенты:
Доктор технических наук, профессор, факультет педагогики, психологии и коммуникативистики Куб ГУ, г. Краснодар,
Ю.И. Дударев
Кандидат педагогических наук, профессор кафедры «Информатика и ЭММ» Южного института менеджмента, г. Краснодар,
Б.А. Бурняшов
Савчук С.Б.
С13 Ряды. Учебно-методическое пособие. – Краснодар: ЮИМ, 2012. –32с.
В учебно-методическом пособии разработаны обучающий и контролирующий блоки, содержащие материал, соответствующий содержанию 6-го раздела «Ряды» учебной дисциплины «Математический анализ». Предложены тезисы-лекции, решения типовых упражнений, задания для самостоятельной работы студентов, а также варианты тестов.
Пособие предназначено для подготовки студентов направлений 080100 Экономика, 080200 Менеджмент,100400 Туризм. Оно также может быть использовано преподавателями «Математического анализа» и «Математики» в учебном процессе при систематизации учебного материала и для контроля уровня усвоения данной темы.
Рекомендовано к изданию научно-методическим советом
(протокол № 10 от 14. 06. 2012 г.)
Ó Издательство ЮИМ
Содержание
Пояснительная записка. 4
Обучающий блок. 5
Содержание лекций (тезисы) 5
Практические занятия. 14
Контролирующий блок. 25
Литература. 31
Пояснительная записка
Структура учебно-методического пособия содержит обучающий блок и контролирующий блок.
В обучающем блоке структурирован учебный материал по нескольким ведущим темам раздела «Ряды». Это позволяет систематизировать большой объем учебного материала в единую логически связанную систему. Каждая тема разбита на отдельные вопросы, определенная часть которых изучается, как правило, в течение одной лекции. Материал этого блока представлен в форме тезисов. Для выработки навыков на практических (семинарских) занятиях предлагаются решения типовых упражнений.
Контролирующий блок состоит из контрольного тестирования.
Разработанные блоки носят как учебно-методический, так и чисто практический характер. Не претендуя на полноту и окончательность теоретического и практического содержания дисциплины, пособие, по мнению авторов, должно способствовать более четкому и содержательному представлению курса Математического анализа, повысить качество формирования у студентов общекультурных и профессиональных компетенций, системы математических знаний и умений, являющихся составными компонентами экономических знаний и умений, а также способствовать повышению методической компетентности преподавателей.
Обучающий блок
Содержание лекций (тезисы)
Лекция 6.1 «Ряды»
Вопросы:
1.Числовые ряды.
2.Основные понятия.
3.Сходимость ряда.
4.Ряды с членами произвольного знака
Определение. Числовым рядом называется бесконечная последовательность чисел u1, u2, …, un, …, соединенных знаком сложения: 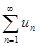 , где un, – n-й член ряда.
, где un, – n-й член ряда.
Числовой ряд задан, если задан его общий член как функция натурального аргумента  , или, если выписано несколько первых членов этого ряда.
, или, если выписано несколько первых членов этого ряда.
Сумма первых n членов  называется частичной суммой ряда.
называется частичной суммой ряда.
Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, то есть  ,
,  – сумма ряда. Тогда
– сумма ряда. Тогда  , в противном случае – расходящимся.
, в противном случае – расходящимся.
Свойства сходящихся рядов:
1. Если ряд  (упрощенная запись) сходится и его сумма равна S, то сходится и ряд
(упрощенная запись) сходится и его сумма равна S, то сходится и ряд  и его сумма равна λS.
и его сумма равна λS.
2. Пусть ряды 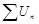 и
и  сходятся. Их суммы
сходятся. Их суммы  и
и  . Тогда сходится и ряд
. Тогда сходится и ряд  .
.
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
4. Пусть  (n-й остаток ряда), тогда сумму ряда можно записать
(n-й остаток ряда), тогда сумму ряда можно записать  . Для того, чтобы ряд
. Для того, чтобы ряд  сходился, необходимо и достаточно, чтобы при
сходился, необходимо и достаточно, чтобы при 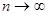 остаток ряда стремился к нулю, то есть
остаток ряда стремился к нулю, то есть  .
.
Необходимый признак сходимости ряда.
Теорема. Если ряд  сходится, то
сходится, то  .
.
Следствие. Если  , то ряд
, то ряд  расходится.
расходится.
Достаточные признаки сходимости положительных рядов ( ).
).
1. Признаки сравнения положительных рядов. Рассмотрим ряды  и
и  , удовлетворяющие условиям
, удовлетворяющие условиям  ,
,  ,
,  для любых n.
для любых n.
1.1. Тогда из сходимости ряда  следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда  .
.
1.2. Если существует 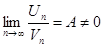 , то ряды
, то ряды  и
и  сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
1.3. Если  для любых n, то из сходимости ряда
для любых n, то из сходимости ряда 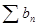 следует сходимость ряда
следует сходимость ряда  , а из расходимости
, а из расходимости  следует расходимость
следует расходимость 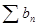 .
.
2. Признак Коши. Пусть  , тогда:
, тогда:
1) если  , то ряд
, то ряд  сходится;
сходится;
2) если  , то ряд
, то ряд  расходится;
расходится;
3) при  признак не работает.
признак не работает.
3. Признак Даламбера. Пусть  , тогда:
, тогда:
1) если  , то ряд
, то ряд  сходится;
сходится;
2) если  , то ряд
, то ряд  расходится;
расходится;
3) если  , то признак не работает.
, то признак не работает.
4. Интегральный признак Коши. Пусть члены ряда  удовлетворяют условию
удовлетворяют условию  и пусть
и пусть  - непрерывная, невозрастающая функция и такая, что
- непрерывная, невозрастающая функция и такая, что  ,
,  …
…  . Тогда несобственный интеграл
. Тогда несобственный интеграл  и ряд
и ряд  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Определение. Ряд называется знакопеременным, если он имеет бесконечное число как положительных, так и отрицательных членов.
Знакочередующийся ряд:  ,
,
где  .
.
Теорема. (Признак Лейбница). Если члены ряда удовлетворяют условию  и
и  , то ряд
, то ряд  сходится, а его сумма
сходится, а его сумма  .
.
Теорема (достаточный признак сходимости знакопеременного ряда). Если  сходится, то сходится и
сходится, то сходится и  .
.
Определение. Ряд  называется абсолютно сходящимся, если ряды
называется абсолютно сходящимся, если ряды  и
и  сходятся. Ряд
сходятся. Ряд  называется условно сходящимся, если ряд
называется условно сходящимся, если ряд  сходится, а ряд
сходится, а ряд  расходится.
расходится.
Ряд  называется функциональным рядом. Функции
называется функциональным рядом. Функции  определены на множестве А. Множество значений x, при которых ряд
определены на множестве А. Множество значений x, при которых ряд  сходится, называется областью сходимости B функционального ряда, и сумма ряда в области B является функций от x,
сходится, называется областью сходимости B функционального ряда, и сумма ряда в области B является функций от x,  .
.
 – частичные суммы ряда. Если предел последовательности частичных сумм существует для любых x из множества B
– частичные суммы ряда. Если предел последовательности частичных сумм существует для любых x из множества B  , то ряд называется сходящимся.
, то ряд называется сходящимся.
На языке кванторов это определение запишется так:
 .
.
Это означает, что для разных значений 
 при одном и том же
при одном и том же  найдутся разные значения номера N, т. е.
найдутся разные значения номера N, т. е.  .
.
Определение. Говорят, что последовательность  сходится равномерно к функции
сходится равномерно к функции  на множестве Е, если для любого сколь угодно малого положительного
на множестве Е, если для любого сколь угодно малого положительного  существует такой номер N, зависящий от
существует такой номер N, зависящий от  , что при любом n больше N (
, что при любом n больше N ( ) и любом x из множества B выполняется неравенство
) и любом x из множества B выполняется неравенство  . Это определение можно записать на языке кванторов так:
. Это определение можно записать на языке кванторов так:

 .
.
Определение. Ряд  сходится равномерно на множестве Е к сумме
сходится равномерно на множестве Е к сумме  , если последовательность его частичных сумм
, если последовательность его частичных сумм  сходится равномерно на множестве Е к сумме
сходится равномерно на множестве Е к сумме  .
.
Теорема (критерий Коши равномерной сходимости). Для того чтобы ряд  сходился равномерно на множестве Е, необходимо и достаточно, чтобы для любого
сходился равномерно на множестве Е, необходимо и достаточно, чтобы для любого  существовал такой номер N (
существовал такой номер N ( ), что при соблюдении условий
), что при соблюдении условий  ,
,  и
и  выполняется неравенство
выполняется неравенство
 .
.
Теорема (признак Вейерштрасса; достаточный признак равномерной сходимости рядов). Если члены ряда  удовлетворяют неравенствам
удовлетворяют неравенствам  , где
, где  ,
,  – числа, не зависящие от x, и если ряд
– числа, не зависящие от x, и если ряд  сходится, то ряд
сходится, то ряд  сходится на множестве Е равномерно.
сходится на множестве Е равномерно.
Свойства равномерно сходящихся рядов:
Теорема 1. Если функции  определены и непрерывны на множестве Е и ряд
определены и непрерывны на множестве Е и ряд  сходится равномерно к сумме
сходится равномерно к сумме  множестве Е, то функция
множестве Е, то функция  непрерывна на Е.
непрерывна на Е.
Теорема 2. Если функции  непрерывны на множестве
непрерывны на множестве 
 n и ряд
n и ряд  на множестве
на множестве  сходится равномерно к сумме
сходится равномерно к сумме  , то его можно почленно интегрировать, то есть
, то его можно почленно интегрировать, то есть  .
.
Теорема 3. Пусть функции 
 n определены на отрезке
n определены на отрезке  и на интервале
и на интервале  существуют непрерывные производные
существуют непрерывные производные  . Если на множестве
. Если на множестве  ряд
ряд  сходится и ряд
сходится и ряд  сходится равномерно, то и сумма ряда
сходится равномерно, то и сумма ряда  имеет на
имеет на  производную, причем
производную, причем  .
.
Лекция 6.2 «Ряды»
Вопросы:
1.Степенные ряды.
2.Область сходимости степенного ряда.
3.Ряд Маклорена
Определение:  - степенной ряд, где
- степенной ряд, где  – числа. Совокупность тех значений х, при которых степенной ряд сходится, называется областью сходимости степенного ряда.
– числа. Совокупность тех значений х, при которых степенной ряд сходится, называется областью сходимости степенного ряда.
Область сходимости степенного ряда устанавливается теоремой Абеля:
1. Если степенной ряд сходится при значении  , то он сходится и притом абсолютно, при всех значениях х таких, что
, то он сходится и притом абсолютно, при всех значениях х таких, что  .
.
2. Если степенной ряд расходится при значении  , то он расходится при всех значениях х таких, что
, то он расходится при всех значениях х таких, что  .
.
Из теоремы Абеля следует, что существует число  , что при
, что при  ряд сходится, а при
ряд сходится, а при  расходится. Величину R называют радиусом сходимости. (-R, R) – интервал сходимости степенного ряда.
расходится. Величину R называют радиусом сходимости. (-R, R) – интервал сходимости степенного ряда.
При значениях  и
и  ряд может, как сходиться, так и расходиться.
ряд может, как сходиться, так и расходиться.
 .
.
Свойства степенных рядов:
Пусть на любом множестве  функция
функция  является непрерывной, тогда
является непрерывной, тогда
1) степенной ряд можно почленно интегрировать на этом отрезке,  ;
;
2) в интервале сходимости степенной ряд можно почленно дифференцировать,
 .
.
После интегрирования и дифференцирования, полученные ряды имеют тот же радиус сходимости R.
Ряд Маклорена. Пусть функция f(x) является суммой степенного ряда  .
.
При х=0  .Найдем коэффициенты Cn. Для этого вычислим производные функции в нуле.
.Найдем коэффициенты Cn. Для этого вычислим производные функции в нуле.
Тогда  .
.
Данный ряд называется рядом Маклорена. Не любая  может быть разложена в ряд Маклорена.
может быть разложена в ряд Маклорена.
Теорема. Для того, чтобы ряд Маклорена сходился к функции  , необходимо и достаточно, чтобы при
, необходимо и достаточно, чтобы при 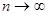 остаток ряда стремился к 0,
остаток ряда стремился к 0,  для всех значений х из интервала сходимости.
для всех значений х из интервала сходимости.
Замечание. Ряд Маклорена – частный случай ряда Тейлора.
 .
.
Ряд Тейлора тесно связан с формулой Тейлора:
 ,
,
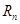 - остаточный член формулы Тейлора
- остаточный член формулы Тейлора
 ,
,  .
.
Остаток ряда Тейлора  равен остаточному члену
равен остаточному члену  формулы Тейлора.
формулы Тейлора.
Лекция 6.3 «Ряды»
Вопросы:
1.Применение рядов в приближенных вычислениях
Вычисление с заданной точностью значения функций.
Пример. Вычислить приближенно  с точностью до 0,0001.
с точностью до 0,0001.
Решение. Применим разложение функции в ряд Маклорена  .
.
При  получим
получим 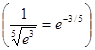 и знакочередующийся ряд
и знакочередующийся ряд  .
.
По признаку Лейбница 1)  ,
,
2)  .
.
Значит, ряд сходится, его сумма  .
.
 =1-0,60000+0,80000-0,03600+0,00540-0,000648-0,0000648-…
=1-0,60000+0,80000-0,03600+0,00540-0,000648-0,0000648-…
Поскольку остаток ряда rn есть знакочередующийся и сходящийся ряд, то по признаку Лейбница его величина (сумма ряда) будет по абсолютной величине не больше (n+1)-го члена ряда. Тогда
 0,0000648<0,0001,.
0,0000648<0,0001,.
 = 0,548752 ≈ 0,5488.
= 0,548752 ≈ 0,5488.
Приближенное вычисление интегралов «неберущиеся» в квадратурах.
Вычислить интеграл  с точностью до 0,0001.
с точностью до 0,0001.
Решение. В разложении  заменим х на –х. Получим
заменим х на –х. Получим
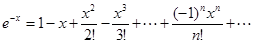 .
.
Тогда
 .
.
Перейдем к сумме интегралов, получим

=  =
=
= 0,66667 - 0,40000 + 0,14286 - 0,03704 + 0,00758 - 0,00128 + 0,00018 - …≈ 0,37897.
Для выполнения точности вычисления оставляем пять знаков после запятой. Результат округляем согласно правилу округления чисел, получим  =0,3790.
=0,3790.
Интегрирование линейных дифференциальных уравнений с переменными коэффициентами (выше первого порядка)  , вообще говоря, не приводится к квадратурам, а их решения не выражаются через элементарные функции.
, вообще говоря, не приводится к квадратурам, а их решения не выражаются через элементарные функции.
Одним из методов интегрирования таких уравнений, важных для приложений, является представление искомого решения в виде степенного ряда.
Теоремы об аналитических решениях.
Теорема 1. Если все коэффициенты и правая часть линейного уравнения n- го порядка

с начальными условиями
 ,
,  , …
, … 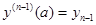
являются аналитическими функциями в точке  (разлагаются в степенные ряды по степеням
(разлагаются в степенные ряды по степеням  в некоторой окрестности этой точки), то решение этого уравнения тоже является аналитической функцией в упомянутой окрестности.
в некоторой окрестности этой точки), то решение этого уравнения тоже является аналитической функцией в упомянутой окрестности.
Теорема 2. Если правая часть уравнения  ,
,  , являются аналитической функцией переменных х и у в точке
, являются аналитической функцией переменных х и у в точке  ,
,  (разлагается в степенной ряд по степеням
(разлагается в степенной ряд по степеням  ,
,  в некоторой окрестности этой точки), то существует единственное решение
в некоторой окрестности этой точки), то существует единственное решение  этого уравнения с начальным условием, являющееся аналитическим в точке
этого уравнения с начальным условием, являющееся аналитическим в точке  .
.
Аналогичное утверждение справедливо и для уравнения  с начальными условиями
с начальными условиями  ,
,  ,…
,… 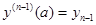 .
.
Практическое получение решения дифференциального уравнения в виде степенного ряда.
1). Способ последовательного дифференцирования: Искомое решение  разлагается в степенной ряд по степени
разлагается в степенной ряд по степени  . Как всякий степенной ряд, он служит рядом Тейлора своей суммы, а по тому разложение имеет вид
. Как всякий степенной ряд, он служит рядом Тейлора своей суммы, а по тому разложение имеет вид 
В случае уравнения n- го порядка первые n коэффициентов  ,
,  …
…  заданы начальными условиями. Подставляя в дифференциальное уравнение
заданы начальными условиями. Подставляя в дифференциальное уравнение  , находят
, находят  . Далее последовательно дифференцируя уравнение и, подставляя после каждого дифференцирования
. Далее последовательно дифференцируя уравнение и, подставляя после каждого дифференцирования  , находят
, находят  ,
,  , завершается нахождение общего закона построения коэффициентов.
, завершается нахождение общего закона построения коэффициентов.
2). Способ сравнивания коэффициентов: Искомое решение разлагается в степенной ряд
 .
.
Из начальных условий определяются коэффициенты
 ,
,  ,
,  ,
,  .
.
Подставляют в дифференциальное уравнение вместо у, ее производных и прочих функций, входящих в уравнение, их разложение в степенные ряды по степеням  и приравнивают коэффициенты при одинаковых степенях
и приравнивают коэффициенты при одинаковых степенях  , определяя из полученных уравнений коэффициенты ряда.
, определяя из полученных уравнений коэффициенты ряда.
Практические занятия
Семинарское занятие 6.1
Числовые ряды. Знакочередующиеся ряды
1. Определить сходимость рядов:
1).  ;2).
;2).  .
.
Решение. 1).  .
.
 ;
;  . Следовательно, ряд расходится.
. Следовательно, ряд расходится.
2).  , Сравним данный ряд с гармоническим рядом
, Сравним данный ряд с гармоническим рядом  . Применим предельный признак сравнения
. Применим предельный признак сравнения  ;
;  . Следовательно, данный ряд расходится.
. Следовательно, данный ряд расходится.
2. Определить сходимость ряда, применяя признак Даламбера:
1)  ;
;
2)  .
.
Решение. 1).  ;
;
 ,
,  .
.
Следовательно, ряд сходится.
2).Ряд сходится, потому что  и
и
 .
.
3. Используя признак Коши, определить сходимость рядов:
1).  ;
;
Решение. 1).  ;
;  =
=  =1/2<1.
=1/2<1.
Ряд сходится.
4. Определить сходимость рядов, применяя интегральный признак Коши:
1). 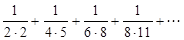 ;
;
2). 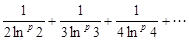 .
.
Решение. 1). Общий член ряда  . Рассмотрим функцию
. Рассмотрим функцию  . Эта функция выполняет все требования теоремы Коши: непрерывна, положительна, монотонно убывающая. (Такую проверку надо делать всегда.)
. Эта функция выполняет все требования теоремы Коши: непрерывна, положительна, монотонно убывающая. (Такую проверку надо делать всегда.)
Вычислим несобственный интеграл
 = =
= =  =
=  =
=
=  . Значит, несобственный интеграл является сходящимся, следовательно, сходится и данный ряд.
. Значит, несобственный интеграл является сходящимся, следовательно, сходится и данный ряд.
2). Общий член ряда  . Рассмотрим функцию
. Рассмотрим функцию  . Она удовлетворяет условиям теоремы Коши. Вычислим несобственный интеграл
. Она удовлетворяет условиям теоремы Коши. Вычислим несобственный интеграл
 =
=  = =
= =  . При параметре
. При параметре  имеем интеграл
имеем интеграл  ,который является расходящимся.
,который является расходящимся.
Таким образом, при параметре  ряд сходится.
ряд сходится.
5. Установить сходимость рядов:
1.  ;
;
2.  ;
;
Решение. 1. Ряд, составленный из абсолютных величин, имеет вид  , общий член
, общий член  . Сравним его с общим членом расходящегося ряда
. Сравним его с общим членом расходящегося ряда  .
.  . Следовательно, ряд
. Следовательно, ряд 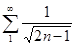 расходится.
расходится.
Применим признак Лейбница к данному знакопеременному ряду. Получим U1>U2>U3>…>0, 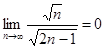 , значит, ряд сходится. И так как расходится ряд, составленный из абсолютных величин, то данный ряд сходится условно.
, значит, ряд сходится. И так как расходится ряд, составленный из абсолютных величин, то данный ряд сходится условно.
Ответ. Сходится условно.
2. По признаку Лейбница получим, что
 , следовательно, ряд сходится. Так как ряд
, следовательно, ряд сходится. Так как ряд  расходится (по интегральному признаку Коши он расходится одновременно с несобственным интегралом
расходится (по интегральному признаку Коши он расходится одновременно с несобственным интегралом 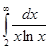 ), то исходный ряд сходится условно. (Ответ).
), то исходный ряд сходится условно. (Ответ).
6. Определить характер сходимости рядов:
1).  ,
,  ; 2).
; 2).  ,
,  .
.
Решение. 1. Применим признак Вейерштрасса, получим  . Ряд
. Ряд  - сходится, значит, ряд
- сходится, значит, ряд  сходится равномерно при
сходится равномерно при  .
.
2. Вычислим модуль отношения последующего и предыдущего членов ряда, получим  . Предел этого отношения равен
. Предел этого отношения равен  . Следовательно, ряд сходится равномерно при любом значении х.
. Следовательно, ряд сходится равномерно при любом значении х.
Задания для аудиторной работы
1. Исследовать на сходимость ряды с помощью признаков сравнения и необходимого признака сходимости:
1.. 
2.. 
3.. 
4.. 
5.. 
2. Определить сходимость рядов, применяя признак Даламбера:
1.  ;
;
2.  ;
;
3.  ;
;
4. 
3. Определить сходимость рядов, применяя признак Коши:
1.  ;
;
2.  ;
;
3.  .
.
4. 
4. Исследовать знакопеременный ряд на условную и абсолютную сходимость:
1.  ;
;
2.  .
.
3. 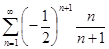 ;
;
4.. 
Семинарское занятие 6.2
Степенные ряды
1. Определить радиус сходимости ряда  .
.
Решение.  . Вычислим предел
. Вычислим предел
 .
.
По признаку Даламбера ряд будет сходиться при значении предела  . Откуда
. Откуда  , значит, радиус сходимости равен R=
, значит, радиус сходимости равен R=  .
.
Ответ. R=  .
.
2. Определить область сходимости ряда  ,
,  .
.
Решение. 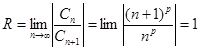 . Значит, ряд сходится при
. Значит, ряд сходится при  и расходится при
и расходится при  .
.
Пусть х =1. Тогда ряд имеет вид  , он сходится при
, он сходится при  и расходится при
и расходится при  .
.
Пусть  . Тогда
. Тогда  - знакочередующийся ряд, и он сходится по признаку Лейбница.
- знакочередующийся ряд, и он сходится по признаку Лейбница.
Ответ. При  область сходимости
область сходимости  , при
, при  область сходимости
область сходимости  .
.
3. Найти радиус и область сходимости  .
.
Решение.
 ,
,
интервал сходимости  .
.
Пусть  . Тогда получим числовой ряд
. Тогда получим числовой ряд  . Его общий член стремится к бесконечности при n→∞. Следовательно, необходимые условия сходимости ряда не выполняются. Ряд расходится.
. Его общий член стремится к бесконечности при n→∞. Следовательно, необходимые условия сходимости ряда не выполняются. Ряд расходится.
Ответ.  ,
,  .
.
Задания для аудиторной работы
Найдите радиус сходимости и область сходимости степенного ряда:
1).  ; 2)
; 2)  .; 3).
.; 3). 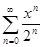 ;
;
4)  .; 5).
.; 5).  ; 6).
; 6).  ;
;
7)  .; 8)
.; 8)  .; 9)..
.; 9).. 
Семинарское занятие 6.3
Разложение функций в ряд Маклорена
1. Написать ряд Тейлора функции  по степеням
по степеням  .
.
Решение. Вычислим значение функции  при х=1, получим
при х=1, получим  .
.
Вычислим производные функции при х=1, получим
 ,
,  ,
,
 ,
,  ,
,
 ,
,  , …,
, …,
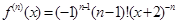 ,
,  .
.
Тогда данная функция раскладывается в следующий ряд
 .
.
(Ответ).
2. Разложить в ряд Маклорена функцию  по степеням х.
по степеням х.
Решение. Разложим в ряд функцию  , получим
, получим  , он сходится при
, он сходится при  . Тогда
. Тогда
 (Ответ.)
(Ответ.)
3. Применяя почленное дифференцирование найти сумму  ряда
ряда  .
.
Решение.  (сумма геометрического ряда со знаменателем x2, ряд сходится при │х│<1). Так как
(сумма геометрического ряда со знаменателем x2, ряд сходится при │х│<1). Так как  , то
, то
 .Ответ.
.Ответ.  .
.
4. Найти сумму ряда  .
.
Решение.  (сумма геометрического ряда со знаменателем
(сумма геометрического ряда со знаменателем  , ряд сходится при
, ряд сходится при  ).
).
Тогда 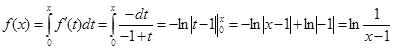 .
.
Ответ.  .
.
5. Применяя почленное дифференцирование ряда, показать, что функция  является решением дифференциального уравнения
является решением дифференциального уравнения  .
.
Решение. Вычислим производную функции y, получим  , тогда
, тогда 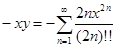 , а вторая производная функции равна
, а вторая производная функции равна
 .
.
Подставляя данные вычисления в дифференциальное