1.Пусть A – матрица размера m x n. Тогда транспонированной матрицей называется такая матрица B размера n x m, что 
, где 
Транспонированная матрица А обозначается 
. Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются местами. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом – вторая строка исходной матрицы и т.д. Например,
Свойства операции транспонирования матриц
2. Произведением матрицы А размера m x n на матрицу B размером n x k называется матрица С размера m x k, элементы которой вычисляются по формуле:
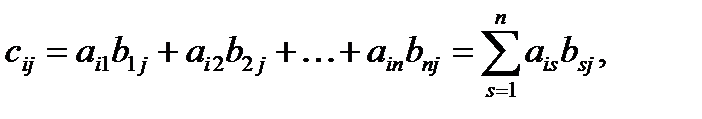где 
Произведение матриц определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.
Число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.
Правило вычисления элементов произведения можно сформулировать следующим образом.
Для того чтобы вычислить элемент произведения, стоящий в i -ой строке и j -ом столбце, нужно взять i -ую строку первого сомножителя и j -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить, т.е. cij=ai1 b1j + ai2 b2j +ai3·b3j + …+ ain·bnj.
В общем случае А×В ¹ В×А
Для операции умножения матриц справедливы следующие свойства:
1) А×(В×С) = (А×В)×С.
2) a×(А×В) = (a×А)×В, a - константа.
3) (А+В)×С = А×С+В×С.
Из существования А×В не следует существование В×А. В частном случае, когда А×В = В×А, говорят, что матрицы А и В коммутативны.
Пример.
Вычислить произведение данных матриц.
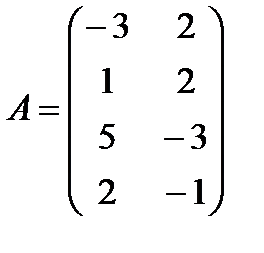
Решение.
1. Выясним,определено ли произведение данных матриц. Число столбцов первого сомножителя – 2, оно равно числу строк второго сомножителя. Следовательно, произведение определено. В результате умножения число строк результата будет равно числу строк первого сомножителя - 4, а число столбцов результата будет равно числу столбцов второго сомножителя – тоже 4, т.е. в результате получится квадратная матрица 4-го порядка.
2. Выполним умножение матриц, пользуясь правилом:
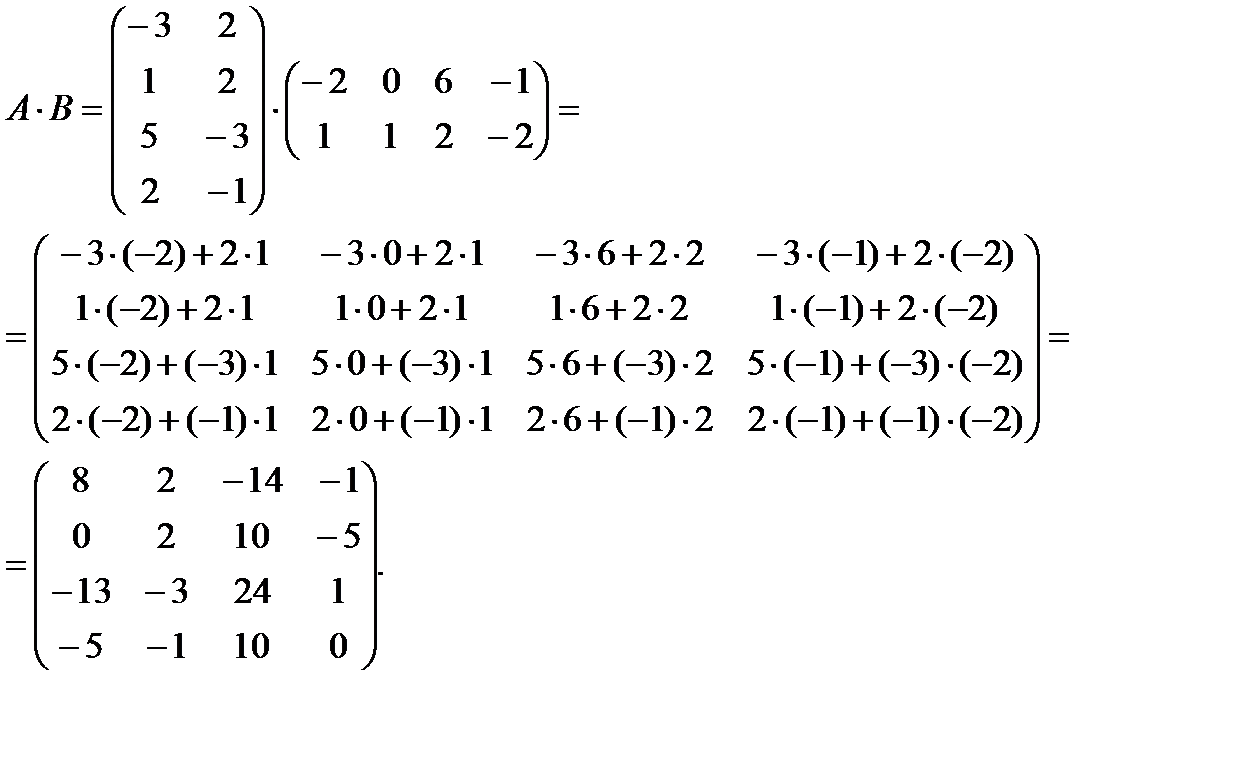
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850г.
Где же в настоящее время применяются матрицы?
Таблица умножения - это не что иное, как произведение матриц (1,2,3,4,5,6,7,8,9)Т ×(1,2,3,4,5,6,7,8,9).
В физике и других прикладных науках матрицы – являются средством записи данных и их преобразования. В программировании – в написании программ. Они еще называются массивами. Широко применение и в технике. Например, любая картинка на экране – это двумерная матрица, элементами которой являются цвета точек.
В психологии понимание термина сходно с данным термином в математике, но взамен математических объектов подразумеваются некие "психологические объекты" – например, тесты.
Кроме того, матрицы имеет широкое применение в экономике, биологии, химии и даже в маркетинге.
Матричное исчисление играет большую роль в решении ряда прикладных задач. На нем базируется, например, такой крупный раздел, как теория колебаний в электрических, акустических и механических системах, где фундаментальное значение имеют характеристические уравнения, собственные значения и собственные векторы. К задачам линейной алгебры сводятся многочисленные алгоритмы обработки экспериментальных данных, минимизации линейных форм, различные задачи теории прочности, упругости и пластичности. Матричное исчисление положено в основу математического аппарата квантовой и статической механики, квантовой физики, радиоэлектроники. Одно из первых направлений в квантовой механике, заложенное Гейзенбергом, даже носило название матричной механики.
Определитель матрицы.
Важнейшей числовой характеристикой квадратной матрицы является определитель (детерминант), который для матрицы Anхn обозначается следующим образом:
Размерность матрицы, для которой ищется определитель, задает его порядок.
Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.
Определитель второго порядка записывается так:
Определителем 3-го порядка, соответствующим матрице 3-го порядка, называется число:
Вычисление определителя 3-го порядка по данной формуле называется правилом треугольников. Состоит оно в следующем: положительные слагаемые суммы получаются как произведение элементов определителя, лежащих на главной диагонали и в углах равнобедренных треугольников, основания которых параллельны главной диагонали; отрицательные слагаемые суммы получаются как произведение элементов, лежащих на побочной диагонали и в углах равнобедренных треугольников, основания которых параллельны этой диагонали.
| “+” |
| “_“ |
Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае - матрица вырожденная или особая.
Наряду с правилом треугольников для вычисления определителя матрицы третьего порядка используется правило Саррюса, которое призвано внести в процесс вычисления определителя наглядность, уменьшив тем самым вероятность возникновения ошибки. Правило названо по имени французского математика Пьера Фредерика Саррюса.
Для матрицы 
детерминант находится суммированием шести произведений из трёх элементов.
Действие выполняется согласно следующей схеме:
первые два столбца определителя записываются справа от определителя. Произведения элементов, стоящих на линиях с пометкой «плюс», складываются, затем из результата вычитаются произведения элементов, находящихся на линиях с пометкой «минус»:
| _ |
| _ |
| _ |
| + |
| + |
| + |
Данный метод применим лишь для определителей третьего порядка, вычислять методом Саррюса определители более высоких порядков нельзя. Однако в октябре 2000 года мексиканский математик Густаво Вильялобос Эрнандес из Гвадалахарского университета нашёл метод, сходный с правилом Саррюса, для вычисления определителей четвёртого порядка и доказал, что вычислять определители пятого порядка подобным методом уже нельзя.
Свойства определителей.
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е. транспонировать определитель (свойство характеризует равноправие строк и столбцов определителя).
2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный:
3. Если в определителе есть нулевая строка (столбец), то определитель равен нулю.
4. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
5. Общий множитель любой строки (столбца) можно выносить за знак определителя.
6. Определитель с пропорциональными строками (столбцами) равен нулю
7. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится.
8. Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали – нули, равен произведению элементов главной диагонали.
В литературе описываются и другие свойства определителей. Предлагаю найти самостоятельно и дополнить список указанных свойств определителей.