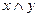Пусть задано универсальное множество I. Тогда для любых множеств  выполняются следующие свойства:
выполняются следующие свойства:
коммутативные законы:
1.  ; 2.
; 2.  ;
;
ассоциативные законы:
3.  ;
;
4.  ;
;
дистрибутивные законы:
5.  ;
;
6.  ;
;
законы идемпотентности:
7.  ; 8.
; 8.  ;
;
законы де Моргана:
9.  ; 10.
; 10. 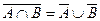 ;
;
законы нуля:
11.  ; 12.
; 12.  ;
;
законы единицы:
13.  ; 14.
; 14.  ;
;
законы поглощения:
15.  ; 16.
; 16.  ;
;
законы дополнения:
17.  ; 18.
; 18.  ;
;
закон двойного дополнения:
19.  .
.
Если  , то множества
, то множества  и
и  называются непересекающимися.
называются непересекающимися.
Булева алгебра
2.1. Логика высказываний
Любая научная теория воспринимается нами как некоторая система понятий и утверждений. Истинность каждого утверждения нуждается в доказательстве, которое в математике проводится с использованием логических средств. Именно эти логические средства изучает раздел математики, называемый математической логикой. Исходным понятием математической логики является понятие высказывания.
Под высказыванием принято понимать повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.
Например, предложение « » - истинное высказывание. Предложение «
» - истинное высказывание. Предложение « » - ложное высказывание. Предложения «
» - ложное высказывание. Предложения « » и «Студенты, ходите на лекции!» высказываниями не являются.
» и «Студенты, ходите на лекции!» высказываниями не являются.
В математической логике интересуются не содержанием высказывания, а его истинностным значением, т.е. его истинностью или ложностью. Для истинностных значений будем использовать следующие обозначения: «1» для истинности и «0» для ложности. Введем в рассмотрение основные логические связки:
| Название | Прочтение | Обозначение |
| Отрицание | не | 
|
| Конъюнкция | и | 
|
| Дизъюнкция | или | 
|
| Импликация | если … то | 
|
| Эквиваленция | тогда и только тогда, когда | 
|
Используя логические связки, из одного или двух высказываний можно образовать новое высказывание, осуществив тем самым логическую операцию. При этом истинностные значения образованных высказываний определяются только истинностными значениями составляющих их высказываний, а не их смыслом.
Пусть  и
и  высказывания. Введем основные логические операции над высказываниями.
высказывания. Введем основные логические операции над высказываниями.
| Название | Обозначение | Прочтение | Когда высказывание, полученное в результате операции, истинно | Когда высказывание, полученное в результате операции, ложно |
Отрицание

|  ( ( ) )
| не 
| если  ложно ложно
| если  истинно истинно
|
Конъюнкция
 и и 
| 
|  и и 
|  и и  оба истинны оба истинны
| в остальных случаях |
Дизъюнкция
 и и 
| 
|  или или 
| в остальных случаях |  и и  оба ложны оба ложны
|
Импликация
 и и 
| 
| если  , то , то  (
( влечет влечет  ,
из ,
из  следует следует  ) )
| в остальных случаях |  истинно, истинно,  ложно ложно
|
Эквиваленция
 и и 
| 
|  тогда и только тогда когда тогда и только тогда когда  (
( эквивалентно эквивалентно  ) )
|  и и  имеют одинаковые значения истинности имеют одинаковые значения истинности
| в остальных случаях |
Операции удобно задавать с помощью таблиц истинности.

| 
| 
| 
| 
| 
| 
|
Высказывательными переменными будем называть такие переменные, значениями которых могут быть любые высказывания. Обозначать высказывательные переменные будем заглавными буквами латинского алфавита  и так далее.
и так далее.
Выражения, содержащие логические операции, назовем формулами. Для каждой формулы можно составить таблицу истинности.
Пример 1. Составить таблицу истинности формулы  .
.

| 
| 
| 
| 
| 
| 
|
Таким образом, значение истинности данной формулы равно 1 при любых значениях истинности высказывательных переменных. Формулы, обладающие таким свойством, называются тавтологиями.
Значение тавтологий состоит, в частности, в том, что они дают правильные способы умозаключений. Например, схема логического умозаключения, выражаемого тавтологией  , часто используется в математике и носит название «доказательство от противного».
, часто используется в математике и носит название «доказательство от противного».
Упражнение. Показать, что следующие формулы являются тавтологиями:
1.  .
.
2.  .
.
Определение. Две формулы  и
и  алгебры высказываний называются равносильными, если при любых значениях истинности переменных
алгебры высказываний называются равносильными, если при любых значениях истинности переменных  истинностные значения высказываний
истинностные значения высказываний 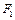 и
и  совпадают.
совпадают.
То, что формулы 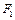 и
и  равносильны, обозначают так:
равносильны, обозначают так:  .
.
Пример 2. Доказать равносильность формул 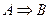 и
и  .
.
Для каждой из данных формул составим таблицу истинности.

| 
| 
| 
|

| 
| 
|
Сравнивая таблицы, видим, что указанные формулы равносильны.
Существует связь между понятием тавтологии и понятием равносильности формул. Она заключается в следующем: формулы 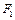 и
и  равносильны тогда и только тогда, когда формула
равносильны тогда и только тогда, когда формула  является тавтологией.
является тавтологией.
Утверждение. Пусть  - произвольные высказывания. Имеют место равносильности:
- произвольные высказывания. Имеют место равносильности:
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. 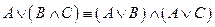 ;
;
6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12. 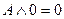 ;
;
13.  ; 14.
; 14. 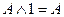 ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  .
.
В качестве упражнения рекомендуем самостоятельно доказать перечисленные равносильности, взяв за образец решение примера 2.
2.2. Понятие булевой функции
Определение. Упорядоченный набор  , где
, где  , называется булевым вектором.
, называется булевым вектором.
Числа  называются координатами вектора, число
называются координатами вектора, число 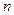 - его длиной. Для булева вектора
- его длиной. Для булева вектора  используется краткое обозначение
используется краткое обозначение  .
.
Множество всех булевых векторов длины 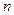 есть единичный
есть единичный 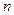 -мерный куб (мы уже рассматривали его в параграфе 1.2). Напомним, что мы обозначили его
-мерный куб (мы уже рассматривали его в параграфе 1.2). Напомним, что мы обозначили его  и показали, что
и показали, что  .
.
Пусть  . Положим
. Положим  . Число
. Число  называется номером булева вектора.
называется номером булева вектора.
Определение. Функция, определенная на  и принимающая значения из множества
и принимающая значения из множества  , называется булевой функцией от
, называется булевой функцией от 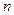 переменных.
переменных.
Для обозначения булевых функций используют строчные латинские буквы. Пишут:  ,
,  ,
,  ,
,  ,
,  .
.
Чтобы задать булеву функцию от 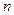 переменных достаточно для каждого набора
переменных достаточно для каждого набора  значений аргументов
значений аргументов 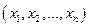 указать соответствующее значение функции. Это удобно делать с помощью таблицы, в строках которой перечислены всевозможные булевы вектора длины
указать соответствующее значение функции. Это удобно делать с помощью таблицы, в строках которой перечислены всевозможные булевы вектора длины 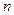 и для каждого набора указано значение функции на этом наборе:
и для каждого набора указано значение функции на этом наборе:

| 
| 
| 
| 
| 
|

| 
| ||||

| 
| ||||

| 
| ||||

| 
| 
| 
| 
| 
|

| 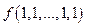
|
Такая таблица называется таблицей истинности функции. Булевы вектора в таблице истинности обычно располагают в порядке возрастания их номеров.
Таблицы, задающие булевы функции от одного числа аргументов, отличаются лишь последним столбцом. Поэтому булеву функцию можно также задавать в виде вектора значений, который выписывается по правому столбцу ее таблицы истинности. Поскольку помимо строки заголовков таблица содержит 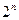 строк (столько, сколько имеется булевых векторов длины
строк (столько, сколько имеется булевых векторов длины 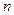 ), то вектор значений булевой функции от
), то вектор значений булевой функции от 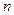 переменных имеет длину
переменных имеет длину 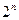 .
.
Утверждение. Число булевых функций от 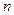 переменных равно
переменных равно  .
.
Доказательство. Булевых функций от 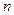 переменных столько, сколько булевых векторов длины
переменных столько, сколько булевых векторов длины 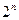 , т.е.
, т.е.  . ■
. ■
Множество булевых функций от 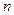 переменных обозначают
переменных обозначают  , множество всех булевых функций -
, множество всех булевых функций -  .
.
Пример 1. Ниже функция  от двух переменных задана в виде таблицы истинности и в виде вектора значений.
от двух переменных задана в виде таблицы истинности и в виде вектора значений.

| 
| 
|
 .
.
То есть, имеем:
 ,
,  ,
,
 ,
,  .
.
Примеры булевых функций
1. Функции одной переменной. Их число:  .
.

| 
| 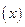
| 
| 
|
Названия функций:
 - константа 0;
- константа 0;
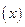 - тождественная функция;
- тождественная функция;
 - отрицание (читается «не
- отрицание (читается «не  »), другое обозначение
»), другое обозначение  ;
;
 - константа 1;
- константа 1;
2. Функции двух переменных. Их число:  .
.

| 
| 
| 
| 
| 
| 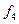
| 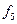
| 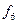
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
Остановимся подробнее на тех функциях двух переменных, которые наиболее часто будут использоваться в дальнейшем:
| Обозначение | Название | Прочтение | |

|  
| конъюнкция | « и и  » »
|
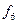
| 
| сложение по модулю 2 | « плюс плюс  » »
|

| 
| дизъюнкция | « или или  » »
|

| 
| стрелка Пирса | «не  или или  » »
|

| 
| эквивалентность | « эквивалентно эквивалентно  » »
|

| 
| импликация | « имплицирует имплицирует  » »
|

| 
| штрих Шеффера | «не  и и  » »
|
Функции  ,
,  ,
,  ,
,  ,
, 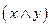 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  обычно называют элементарными. Символы
обычно называют элементарными. Символы  , участвующие в их обозначении, называют логическими связками.
, участвующие в их обозначении, называют логическими связками.
Определение. Говорят, что функция  зависит существенным образом от аргумента
зависит существенным образом от аргумента 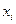 , если существуют такие значения
, если существуют такие значения  переменных
переменных  , что
, что
 .
.
В этом случае переменная 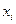 называется существенной переменной. В противном случае ее называют несущественной или фиктивной.
называется существенной переменной. В противном случае ее называют несущественной или фиктивной.
Пример 2. Для функции  переменная
переменная  - фиктивная, а
- фиктивная, а  - существенная.
- существенная.

| 
| 
|
Действительно, имеем:
 ,
,  , следовательно,
, следовательно,  - фиктивная;
- фиктивная;
 , следовательно,
, следовательно,  - существенная.
- существенная.
Операция удаления (введения) фиктивных переменных. Пусть для функции  переменная
переменная 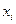 является фиктивной. Возьмем таблицу истинности функции
является фиктивной. Возьмем таблицу истинности функции  и на ее основе построим новую таблицу, вычеркнув все строки, в которых
и на ее основе построим новую таблицу, вычеркнув все строки, в которых  , а также вычеркнув столбец переменной
, а также вычеркнув столбец переменной 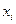 . Полученная таким образом таблица будет определять некоторую функцию
. Полученная таким образом таблица будет определять некоторую функцию  , причем на любом наборе значений
, причем на любом наборе значений  переменных
переменных  для функций
для функций  и
и  выполняется равенство
выполняется равенство  . Говорят, что функция
. Говорят, что функция  получена из функции
получена из функции  путем удаления фиктивной переменной, а также, что
путем удаления фиктивной переменной, а также, что  получена из
получена из  путем введения фиктивной переменной.
путем введения фиктивной переменной.
Определение. Функции  и
и  называются равными, если функцию
называются равными, если функцию  можно получить из функции
можно получить из функции  путем введения или удаления фиктивных аргументов.
путем введения или удаления фиктивных аргументов.
Пример 3. Для функции  переменная
переменная  - существенная, а
- существенная, а  - фиктивная. Вычеркиваем из таблицы истинности функции
- фиктивная. Вычеркиваем из таблицы истинности функции  строчки и столбец, закрашенные серым цветом, получим таблицу истинности для функции
строчки и столбец, закрашенные серым цветом, получим таблицу истинности для функции  . Функции
. Функции  и
и  равны.
равны.
|
|
Замечания. 1.Далее, если число переменных специально не оговаривается, функции рассматриваются с точностью до фиктивных переменных, т.е. предполагается, что с заданием некоторой булевой функции  заданы все равные ей функции, и для обозначения равных функций используется один и тот же функциональный символ.
заданы все равные ей функции, и для обозначения равных функций используется один и тот же функциональный символ.
2. В дальнейшем, рассматривая любую систему функций, будем по умолчанию полагать, что все функции данной системы зависят от одних и тех же переменных. Это позволит избежать громоздкости рассуждений, не нарушив при этом их общности.
2.3. Реализация булевых функций формулами
Функцию  , реализуемую формулой над множеством функций
, реализуемую формулой над множеством функций  , будем называть суперпозицией функций
, будем называть суперпозицией функций  .
.
Пример 1. Формула  реализует функцию
реализует функцию  , заданную таблицей истинности:
, заданную таблицей истинности:

| 
| 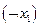
| 
| 
|
Пример 2. Формула  реализует функцию
реализует функцию  , заданную таблицей истинности:
, заданную таблицей истинности:

| 
| 
| 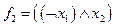
|
Заметим, что формулы  и
и  различны, а реализуемые ими функции
различны, а реализуемые ими функции  и
и  равны.
равны.
Если две формулы  и
и  реализуют равные функции, то они называются равносильными. Равносильность формул обозначают так:
реализуют равные функции, то они называются равносильными. Равносильность формул обозначают так: 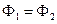 .
.
Замечание. Для упрощения записи формул введены следующие соглашения:
а) внешние скобки у формул можно опускать;
б) вместо  можно писать
можно писать  , а вместо
, а вместо  –
–  или
или  ;
;
в) связку  принято считать сильнее любой двуместной связки, поэтому внешние скобки в выражении, над которым стоит знак «– », можно опускать;
принято считать сильнее любой двуместной связки, поэтому внешние скобки в выражении, над которым стоит знак «– », можно опускать;
г) связку  принято считать сильнее
принято считать сильнее  и
и 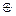 , поэтому выражения
, поэтому выражения  ,
,  ,
,  можно в скобки не брать.
можно в скобки не брать.
Пример 3.
 .
.
Теорема. Для формул над множеством 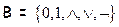 имеют место следующие равносильности:
имеют место следующие равносильности:
1. 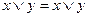 ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. 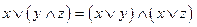 ;
;
6.  ;
;
7. 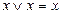 ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  .
.
Доказательство. Все равносильности можно доказать, используя таблицы истинности. Например, равносильность 10:
|
|
Как видим, формулы  и
и  реализуют равные функции и, следовательно, являются равносильными. ■
реализуют равные функции и, следовательно, являются равносильными. ■
Упражнение. Доказать, что имеют место равносильности:
1.  ;
;
2.  ;
;
3.  ;
;
4. 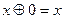 ;
;
5.  ;
;
6.  .
.
2.4. Двойственные функции
Определение. Функция, реализуемая формулой 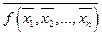 , называется двойственной к функции
, называется двойственной к функции  .
.
Функцию, двойственную к функции  , обозначают
, обозначают  , т.е.
, т.е.  .
.
Пример 1.
а) Пусть 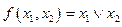 . Тогда
. Тогда
 .
.
б)Пусть  . Тогда
. Тогда
 .
.
в)Пусть  . Тогда
. Тогда  .
.
г)Пусть  . Тогда
. Тогда 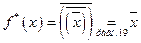 .
.
д)Пусть <