Диаграмма Вышнеградского

Область пространства параметров, каждая точка которой определяет многочлен Гурвица, называется областью устойчивостью. Многочлен Гурвица - многочлен, все нули которого лежат слева от мнимой оси комплексной плоскости. Для системы третьего порядка его можно записать в виде

s³ + А₁s² + А₂s + 1 = 0.

В соответствии с критерием Гурвица А₁А₂ > 1 и система устойчива. Если А₁А₂ = 0, то система находится на границе устойчивости. Граница устойчивости в плоскости параметров А₁ - А₂ есть гипербола и представлена на рис.8.

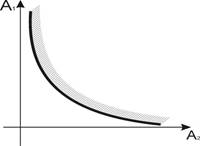
Рис. 6.8

Такая диаграмма называется диаграммой Вышнеградского.

Границы устойчивости

Так как все корни характеристического уравнения D(s) = 0 должны располагаться в левой полуплоскости, то мнимая ось jw плоскости корней служит границей устойчивости. Можно выделить три типа границ устойчивости линейных систем, которые характеризуются, соответственно:

- нулевым корнем s = 0, возникает тогда, когда а₀ = 0; все определители Гурвица положительны, кроме последнего, такая граница называется апериодической;

- парой чисто мнимых корней s_{1, 2} = ± jω, появляется при D_n-1 = 0; все остальные определители Гурвица положительны, колебательная граница устойчивости;

- корнем s = ® ¥, возникает тогда, когда а_n = 0.

Пример:: передаточная функция разомкнутой системы задана в виде

Характеристическое уравнение замкнутой системы

Т₁Т₂ s³ + (Т₁ + Т₂) s² + s + к = 0

и все коэффициенты положительны. Условие устойчивости по критерию Гурвица

(Т₁ + Т₂) > кТ₁Т₂

или

к < (1/T₁ + 1/T₂).

Коэффициент усиления можно взять тем больше, чем меньше постоянные времени.

Выделяем границы устойчивости:

- a₀ = 0, к = 0;

- D_n-1 = 0, к_кр = 1/Т₁ + 1/Т₂;

- a_n = 0, Т₁Т₂ = 0.

Эти три границы устойчивости можно изобразить графически в пространстве параметров к, Т₁ и Т₂ и найти области устойчивости системы.

Пусть Т₁ и Т₂ = const, а к = var. Пространство параметров в этом случае прямая линия (рис. 6.9), а границы устойчивости - точки к = 0 и к_кр = 1/Т₁ + 1/Т₂.

Рис. 6.9

Пусть Т₂ = const, а Т₁ и к = var. Пространство параметров – плоскость Т₁ - к. Первая граница (к = 0) лежит на оси Т₁. Вторая граница 1/Т₁ = к – 1/Т₂ имеет вид гиперболы с асимптотами Т₁ = 0 и

к = 1/Т₁. Третья граница (Т₁ = 0) совпадает с осью к (рис. 6.10).

 

Рис. 6.10

Как видно из рис. 6.10, при увеличении постоянных Т₁ и Т₂ область устойчивости сужается. Отрицательно влияет на устойчивость также и увеличение коэффициента усиления к. При любых заданных Т₁ и Т₂ существует своё к_кр.

Рассмотрим пример определения границ устойчивости системы по критерию Михайлова. Пусть, как и прежде

D(s) = Т₁Т₂ s³ + (Т₁ + Т₂) s² + s + к

Если s = jw, то

D(jw) = P(w) + j Q(w), P(w) = к – (Т₁ + Т₂) w², Q(w) = w - Т₁Т₂w³.

Если характеристическое уравнение системы D(s) = 0 имеет корень s = jw₀, то D(jw₀) = 0 и Р(w) = 0, Q(w) = 0. Графически это означает попадание одной точки кривой Михайлова (w = w₀) в начало координат. Физический смысл величины w = w₀ - частота колебаний системы на границе устойчивости. Очевидно, что все три границы устойчивости можно объединить равенством

Р_i = jw₀, w₀ = 0, w₀ = ¥.

Отсюда для границы устойчивости имеем

к – (Т₁ + Т₂) w² = 0, w - Т₁Т₂w³ = 0.

Из последнего уравнения

w₀ = 0 и w²₀ = 1/(Т₁Т₂).

Тогда из первого уравнения

к = 0 и к = 1/Т₁ + 1/Т₂.

Для бесконечно удалённого корня (w₀ = ¥) получаем Т₁Т₂ = 0. Этот результат совпадает с тем, что был получен по критерию Гурвица.

6.6. Влияние структуры и передаточного

коэффициента системы на устойчивость.

Системы, неустойчивые при любых значениях параметров, называются структурно-неустойчивыми. К таким звеньям относятся:

- интегрирующее звено W(s) = 1/s;

- неустойчивое статическое звено первого порядка W(s) = к/(Ts – 1);

- идеальное колебательное звено W(s) = к /(T² s² + 1)

и ряд других звеньев. Её можно сделать устойчивой, изменив структуру.

ПРИМЕР: определить передаточную функцию интегрирующего звена, охваченного жесткой отрицательной обратной связью (рис. 6.11).

Рис. 6.11

Передаточная функция интегрирующего звена, охваченного единичной отрицательной обратной связью, определяется по выражению

Следовательно, получили абсолютно устойчивое апериодическое звено первого порядка.

Используемый в промышленности ПИ-закон регулирования соответствует параллельному соединению пропорционального и идеального интегрирующего звена

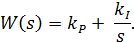
Поэтому влияние этого закона на устойчивость двоякое: при больших значениях коэффициента интегральной составляющей k_I устойчивость хуже, при больших значениях коэффициента k_P – лучше.

Для одноконтурных систем, в которых нет форсирующих звеньев, получено условие структурной устойчивости в виде двух неравенств

q + t < 2 4r <n,

где q – число идеальных интегрирующих, t – число неустойчивых и r – число консервативных звеньев АСР; n – порядок системы.

Для систем со статическими не перекрёстными обратными связями установлено правило: если все контуры системы структурно устойчивы, то и сама система структурно устойчива. Для остальных систем условия структурной устойчивости не найдены.

Рассмотрим влияние передаточного коэффициента разомкнутого контура на устойчивость замкнутой системы. Учтём, что для одноконтурных систем коэффициент k входит в выражение амплитудно-фазовой частотной характеристики W(jw) как множитель

W(jw) = k H(jw) / D (jw).

Это означает, что длина вектора W(jw) при всех значениях w пропорциональна коэффициенту k. При его увеличении АФЧХ расширяется и приближается к критической точке (-1, j0). Следовательно, увеличение k приводит к ухудшению устойчивости системы.

Пример:: для системы с передаточной функцией

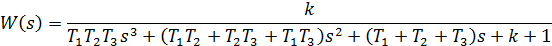
определить значение предельного (критического, граничного) передаточного коэффициента.

В соответствии с критерием Гурвица для систем третьего порядка должно выполняться следующее условие:

(T₁ T₂ + T₂ T₃ + T₁ T₃) (T₁ + T₂ + T₃) - T₁ T₂ T₃ (K + 1) > 0.

Следовательно,

k_КР = (1/T₁ + 1/T₂ + 1/T₃)(T₁ + T₂ + T₃).

В существовании предельного коэффициента передачи k_КР можно убедиться и с помощью критерия Михайлова. Для статических систем а₀ = =1 + k, а для астатических а₀ = 1. Очевидно, что при некотором предельном значении а_n, и, следовательно, коэффициенте k_КР, кривая Михайлова пройдёт через начало координат, т.е. система будет на границе устойчивости (см. рис. 4). Таким образом, установлена одна из важнейших в ТАУ закономерность: чем больше общий передаточный коэффициент разомкнутого контура системы регулирования, тем ближе замкнутая система к границе устойчивости.

Предельное значение передаточного коэффициента системы зависит также от соотношения постоянных времени и не зависит от их абсолютных значений. Предельный коэффициент тем больше, чем больше разность между двумя наиболее различающимися постоянными времени и чем ближе третья постоянная к среднему арифметическому первых двух. На практике “раздвинуть” постоянные времени не всегда удается, или невозможно, или нецелесообразно. Эффективным средством достижения требуемой точности системы при сохранении её устойчивости является изменение структуры системы путём добавления специальных стабилизирующих и корректирующих устройств.

Пример: Задана передаточная функция объекта управления

Как изменятся динамические свойства системы, если вводится форсирующее звено первого порядка с передаточной функцией

W_к(s) = Тs + 1.

Характеристический полином замкнутой системы без коррекции

Следовательно, k<(1/T₁+1/T₂).

Передаточная функция разомкнутого контура с корректирующим звеном

Характеристический полином замкнутого контура

D(s) = Т₁Т₂ s³ + (Т₁ + Т₂) s² + (1 + kТ)s + k.

Из критерия Гурвица следует, что

k/(1 + kТ) < (1/Т₁ + 1/Т₂).

Если kТ >>1, то k можно брать любым.

Если kТ = 1, то значение k_КР увеличивается в два раза.

6.7. Запасы устойчивости по амплитуде и по фазе.

Для надёжного функционирования система должно держаться на определённом расстоянии от границы устойчивости, т.ё. обладать некоторым запасом устойчивости. Это обеспечивает приемлемые статические и динамические характеристики в случае неточного знания модели или дрейфа её параметров (например, коэффициента передачи).

Амплитудно-фазовые характеристики разомкнутых систем могут иметь точки пересечения с вещественной осью как справа, так и слева относительно критической точки (- 1, j0). Следовательно, устойчивость может быть потеряна как при увеличении, так и при уменьшении коэффициента передачи. Критическим значением последнего называется такое его значение, при котором АФЧХ разомкнутого контура проходит через критическую точку (- 1, j0) и система находится на границе устойчивости.

Степень близости устойчивой замкнутой системы к границе устойчивости измеряется:

- минимальным по модулю значением вещественной части корней характеристического уравнения (критерий Гурвица);

- минимальным значением от годографа Михайлова до начала координат (0, j0);

- минимальным расстоянием между годографом Найквиста и точкой Найквиста (-1, j0).

На практике для оценки близости пользуются последним критерием. Для определённости будем считать, что разомкнутая система устойчива.

Для характеристики степени удаления системы от границы устойчивости вводятся понятия о запасах устойчивости. Запасом устойчивости по амплитуде называется величина

DА = 1 – А(w_p)= 1- d,

где w_p - частота, на которой фазовая характеристика равняется ± 180⁰ (рис. 6.12). По физическому смыслу это число, на которое должен быть умножен коэффициент усиления разомкнутой системы k_P, чтобы замкнутая система оказалась на границе устойчивости (если передаточную функцию разомкнутой системы W(jω) умножить на коэффициент 1/d, то диаграмма Найквиста пройдёт через точку - 1,j0 и система окажется на границе устойчивости).

Поэтому существует и такое определение запаса устойчивости по амплитуде: если диаграмма Найквиста для разомкнутой системы пересекает отрицательное направление действительной оси в точке – d и при этом замкнутая система устойчива, то запас по модулю равен 1/d. Если диаграмма Найквиста имеет несколько пересечений отрицательного направления вещественной оси, то запас по модулю определяется по той точке, которая дает наименьшее значение 1/d.

Рис. 6.12

Этот показатель чаще определяют по диаграмме Боде (рис. 13), рассматривая логарифмический запас устойчивости по амплитуде

DL = - L(ω_π) = 20lg A(w_p), ДБ.

Он гарантирует, на сколько децибел может быть поднята логарифмическая амплитудно-частотная характеристика L(ω) разомкнутой системы до границы устойчивости – совпадения частоты среза ω_СР и частоты ω_π.

Рис. 6.13

Зная DL, можно найти граничное значение коэффициента передачи разомкнутой системы k_ГР по формуле:

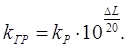
Запас устойчивости по фазе D j(w_СР) называется минимальный угол, на который нужно повернуть АФЧХ разомкнутой системы, чтобы замкнутая система оказалась на границе устойчивости

где j(w_СР) – значение ФЧХ на частоте среза w_СР, т.е. на частоте, где А(w) = 1. Он показывает, на сколько должно увеличиться запаздывание по фазе разомкнутой системы на этой частоте, чтобы замкнутая система находилась на границе устойчивости. Запас определяется по АФЧХ, если с центром в начале координат провести окружность единичного радиуса R1 и определить её точку пересечения с АФЧХ (рис. 6.12).

Для удовлетворительной работы системы принимают DL = 6 - 20 децибел и D j(w_СР)= 30^o – 60^o, в отдельных случаях значения запасов по амплитуде и по фазе могут и отличаться от этих значений. Для определения запасов устойчивости по амплитуде и фазе в MATLAB предусмотрены функции margin(W) и [ dL,dfi,omegapi,omegasr ]= margin(Wz):

>> W=tf([1.5],[1 3 3 1])

Transfer function:

1.5

---------------------

s^3 + 3 s^2 + 3 s + 1

>> margin(W) – рис. 6.14

Рис. 6.14

>> [dL,dfi,omegapi,jmegasr]=margin(W)

dL =

5.3341 → ∆L=20lgdL=20lg5.3341=14.54 ДБ

dfi =

92.6324

omegapi =

1.7322

jmegasr =

0.5571

Для оценки устойчивости можно использовать такой показатель, как минимум возвратной разности, который представляет собой знаменатель передаточной функции замкнутой системы [1+W(jω)]. Если возвратная разность минимальна на частоте, при которой W(jω) имеет вещественное значение, то она непосредственно указывает на запас устойчивости по модулю. Если же она минимальна на частоте, при которой , то это определяет запас устойчивости по фазе. Из рис. 6.15 видно, что минимум возвратной разности – это минимальное расстояние от диаграммы Найквиста до точки -1, j0. Увеличивая это расстояние, мы повышаем устойчивость системы.

Минимум возвратной разности используется при анализе и синтезе систем управления в пространстве состояний, робастных систем и линейно-квадратичных регуляторов.

 

Рис. 6.15

В заключении отметим, что анализ устойчивости линейных систем базируется на теоремах Ляпунова:

- невозмущённое движение ∆ х^*_ВЫХ = 0 устойчиво независимо от вида малых нелинейностей φ, если все корни характеристического уравнения D(s) = 0 имеют отрицательные вещественные части;

- невозмущённое движение ∆ х^*_ВЫХ = 0 неустойчиво независимо от вида малых нелинейностей φ, если хотя бы один корень характеристического уравнения D(p) = 0 имеет положительную вещественную часть.

 

6.8. Исследование устойчивости систем управления в среде MATLAB.

Исследуем устойчивость системы с характеристическим полиномом

Для вычисления корней характеристического полинома можно использовать функцию roots( a ), где а – вектор коэффициентов характеристического полинома:

>> y=roots([1 1 2 10 8])

y =

0.8351 + 2.0229i

0.8351 - 2.0229i

-1.6702

-1.0000

Следовательно, система неустойчива, так как комплексные сопряжённые корни имеют положительную вещественную часть.

Исследуем устойчивость системы с характеристическим полиномом

с помощью критерия Гурвица. Все коэффициенты полинома положительны, рассчитываем главный определитель Гурвица с помощью оператора det(A):

>> A=[2 16 32 0 0;1 9 24 16 0;0 2 16 32 0;0 1 9 24 16;0 0 2 16 32]

A =

2 16 32 0 0

1 9 24 16 0

0 2 16 32 0

0 1 9 24 16

0 0 2 16 32

>> det(A)

ans =

Следовательно, система находится на границе устойчивости. Это подтверждается и расчётами:

s=roots([1 2 9 16 24 32 16])

s =

-0.0000 + 2.0000i

-0.0000 - 2.0000i

0.0000 + 2.0000i

0.0000 - 2.0000i

-1.0000

-1.0000

По заданной передаточной функции

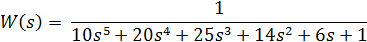
определить, устойчива ли данная система.

Все коэффициенты характеристического уравнения положительны, рассчитываем главный определитель Гурвица и его диагональные миноры:

>> A=[20 14 1 0;10 25 6 0;0 20 14 1;0 10 25 6]

A =

20 14 1 0

10 25 6 0

0 20 14 1

0 10 25 6

>> det(A)

ans =

>> A1=[20 14 1;10 25 6;0 20 14]

A1 =

20 14 1

10 25 6

0 20 14

>> det(A1)

ans =

>> A2=[20 14;10 25]

A2 =

20 14

10 25

>> det(A2)

ans =

Главный определитель Гурвица и все его диагональные миноры положительны. Следовательно, система устойчива. Это подтверждается расчётом корней характеристического полинома

s=roots([10 20 25 14 6 1])

s =

-0.6874 + 0.8806i

-0.6874 - 0.8806i

-0.1775 + 0.5149i

-0.1775 - 0.5149i

-0.2702

и моделированием:

>> W=tf([1],[10 20 25 14 6 1])

Transfer function:

-------------------------------------------

10 s^5 + 20 s^4 + 25 s^3 + 14 s^2 + 6 s + 1

>> step(W) – рис. 16

Рис. 16

>> nyquist(W) – рис. 17

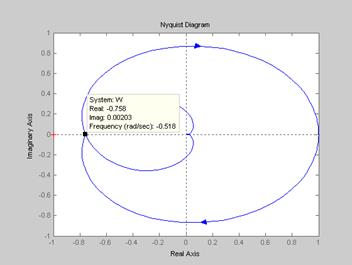
Рис. 17

>> margin(W) – рис. 18

Рис. 18

Рассмотрим замкнутую систему управления:

передаточная функция объекта управления

передаточная функция звена обратной связи

Необходимо определить значение k, при котором система будет находится на границе устойчивости, частоту и период колебаний.

Передаточная функция замкнутой системы управления

,

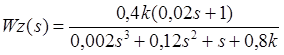граничное значение коэффициента k находится из решения уравнения

0.12 -0.0016 k = 0,

следовательно k = k_ГР = 75. Исследуем систему при k_ГР = 75:

>> Wo=tf([30],[0.1 1 0])

Transfer function:

-----------

0.1 s^2 + s

>> Woc=tf([2],[0.02 1])

Transfer function:

----------

0.02 s + 1

>> Wz=feedback(Wo,Woc,-1)

Transfer function:

0.6 s + 30

-----------------------------

0.002 s^3 + 0.12 s^2 + s + 60

>> pole(Wz)

ans =

-60.0000

0.0000 +22.3607i

0.0000 -22.3607i

Следовательно, частота колебаний ω₀ = 22,3607 с^-1, период колебаний Т₀ = 2π/ω₀ = 2π/22,3607 = 0,281 c.

>> step(Wz) – рис. 19

Рис. 19

Переходный процесс подтверждает расчётные данные.