В данной работе вычисление абсолютной и относительной погрешности проводится при условии, что известно точное значение определенного интеграла. Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами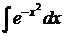 
, 
, 
, 
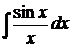и т.д. Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций.
Определенные интегралы от таких функций можно вычислить только приближенно. Для оценки точности вычисления в таких случаях используют, например, правило Рунге. В данном случае интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном 
. Погрешность вычисления значения интеграла при числе шагов, равном , вычисляется по формуле Рунге: 
, для формул прямоугольников и трапеций 
, а для формулы Сипсона 
. Таким образом, интеграл вычисляется для последовательных значений числа шагов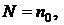 
, 
,..., где 
– начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения 
будет выполнено условие 
, где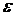 
– заданная точность.
Для того чтобы не вычислять один и тот же интеграл по нескольку раз для разных разбиений отрезка интегрирования, можно вычислить шаг интегрирования заранее.
Пример. Выбрать шаг интегрирования для вычисления интеграла 
с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона.
Квадратурная формула прямоугольников.
Вычислим, при каком шаге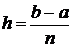 
погрешность будет составлять 0,01:
.
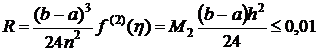Поскольку 
, то 
.
При шаге 
отрезок 
разбивается на 
равностоящих узлов.
Квадратурная формула трапеций.
Вычислим, при каком шаге 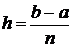погрешность составит 0,01:
.
Поскольку 
, 
.
При шаге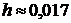 
,отрезок разбивается на 
равностоящих узлов.
Квадратурная формула Симпсона.
Вычислим, при каком шаге 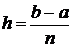погрешность составит 0,01:
,
, 
.
При шаге 
, отрезок разбивается на 
равностоящих узлов.
Как и следовало ожидать, наименьшее количество равностоящих узлов получается при вычислении интеграла по квадратурной формуле Симпсона.
Содержание РГР «Приближенные методы вычисления
Определенных интегралов»
Студенту предлагается работа, состоящая из четырех этапов:
1 этап – точное вычисление определенного интеграла.
2 этап – приближенное вычисление определенного интеграла одним из методов: прямоугольников или трапеций.
3 этап – приближенное вычисление определенного интеграла методом парабол.
4 этап – расчет и сравнение абсолютной и относительной ошибок приближенных методов: 
, где 
– точное решение интеграла, 
– значение интеграла, полученное с помощью приближенных методов.
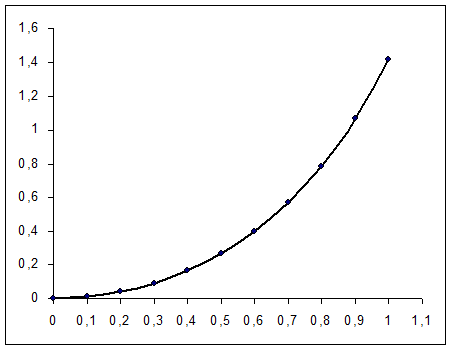
Построение графика подынтегральной функции.
Варианты и образец выполнения РГР приведены ниже.
Варианты
| № варианта | f(x) | a | b | Шаг h |
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
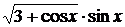
| π | 0,1π | ||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
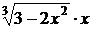
| 0,1 | |||
| π/2 | 0,05π | ||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| π | 0,1π | ||
| 0,1 | |||
| 0,1 | |||
| π/2 | 0,05π | ||
| 0,1 | |||
| π/2 | 0,05π | ||
| 0,1 | |||
| 0,1 | |||
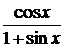
| π/2 | 0,05π | ||
| π/2 | 0,05π | ||
| π/2 | 0,05π | ||
| π/2 | 0,05π | ||
| 0,1 | |||
| 0,1 | |||
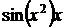
| π/2 | 0,05π | ||
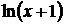
| 0,1 |
Образец выполнения РГР
Задание. Вычислить интеграл 
1. Точное вычисление:
= 0,40631714.
2. Приближенное вычисление с помощью формул прямоугольников:
,
, 
.
, 
.
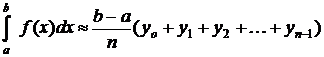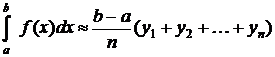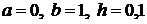Составим таблицу:
| № | xi | yi = f (xi) |
| 0,1 | 0,010005 | |
| 0,2 | 0,04016 | |
| 0,3 | 0,091207 | |
| 0,4 | 0,165041 | |
| 0,5 | 0,265165 | |
| 0,6 | 0,396981 | |
| 0,7 | 0,567851 | |
| 0,8 | 0,786966 | |
| 0,9 | 1,065081 | |
| 1,414214 |
По первой формуле прямоугольников получаем:
≈ 0,1 
= 0,1·3,062514 = 0,306251.
По второй формуле прямоугольников получаем:
≈ 0,1 
= 0,1· 4,802669 = 0,480267.
В данном случае первая формула дает значение интеграла с недостатком, вторая – с избытком.
Вычислим относительную и абсолютную погрешности.
I = 0,40631714, 
, 
, 
.
, 
.
3. Приближенное вычисление по формуле трапеций:
В нашем случае получаем:
≈ 0,1 
= =0,1 
= 0,1·4,095562 = =0,409556.
Вычислим относительную и абсолютную погрешности.
I = 0,40631714,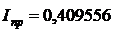 
, 
.
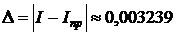4. Приближенное вычисление по формуле Симпсона:
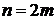
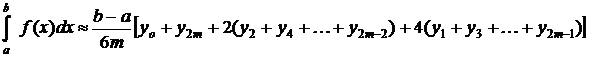
В нашем случае получаем:
≈ 
=
= 
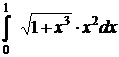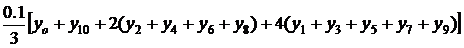= 0,406325.
Вычислим относительную и абсолютную погрешности.
I = 0,40631714 
, 
.
В действительности, 
= 0,40631714.
Таким образом, при разбиении отрезка 
на 10 частей по формуле Симпсона мы получили 5 верных знаков; по формуле трапеций – три верных знака; по формуле прямоугольников мы можем ручаться только за первый знак.
Литература:
1. Задачи и упражнения по математическому анализу для втузов: учеб. пособие для втузов / Г. С. Бараненков [и др.]; под ред. Б.П. Демидовича. - М.; Владимир: Астрель: Изд-во АСТ: ВКТ, 2010. - 495 с.
2. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. Т. 1: Дифференциальное и интегральное исчисления функций одной переменной. Ряды / Л. Д. Кудрявцев. - 3-е изд., перераб. - М.: ФИЗМАТЛИТ, 2009. - 399 с.
3. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов. В 2 т. Т. 1 / Н. С. Пискунов. - Изд. стер. - М.: Интеграл-Пресс, 2004. - 415 с.
4. Шипачев В.С. Высшая математика: учеб. для вузов / В. С. Шипачев. - 7-е изд., стер. - М.: Высш. шк., 2005. - 479 с.
Баранова И.М., Гущин Г.В., Еловиков А.Б., Часова Н.А.
МАТЕМАТИКА
ПРИБЛИЖЕННЫЕ МЕТОДЫВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Методические указания и задания к расчетно-графической работе
для студентов всех направлений подготовки бакалавров
очной формы обучения
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел
Отпечатано: Печатный цех БГИТА