Дифференциальные уравнения являются основной формой представления математических моделей. Дифференциальные уравнения – это уравнения, в котором неизвестная функция входит под знаком производной или дифференциала. Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то уравнение называется обыкновенным. Обыкновенное дифференциальное уравнение в общем случае содержит независимую переменную (Х), неизвестную функцию (Y(X)) и ее производные (dY/dX) до n -ого порядка и имеет вид
F(X,Y,Y',Y",…,Y(n))=0.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.
Рассмотрим технику решения обыкновенных дифференциальных уравнений с начальными условиями, т.е. таких, для которых известны значения искомой функции и ее производных (до n-1 порядка) при Х=0. решение уравнений в такой постановке называется задачей Коши.
Известно, что аналитическое решение дифференциальных уравнений возможно лишь в небольшом числе случаев. В остальных случаях оно доступно только с помощью численных методов. Самый простой из них – метод Эйлера. Решением уравнения является такая функция Y(X), которая, будучи подставленной в уравнение, превращает его в тождество. Само уравнение неизвестно. В начальных условиях задается только одна его точка Y(Xo). Суть метода применительно к дифференциальному уравнению первого порядка dY/dX=Y(X,Y) с начальными условиями Y(Xo)=Yo поясняет рисунок.
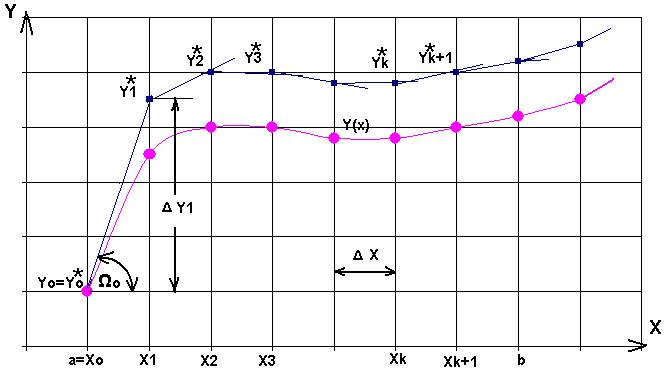
Разобьем весь диапазон интегрирования уравнения на участки с одинаковым шагом ΔХ и попытаемся найти значение искомой функции Y(X) в точке X1=Xo+ ΔХ.
Искомая функция изображена линией с ординатами Yo, Y1, Y2, …, Yk+1 (розовые кружки), а полученная по методу Эйлера – ломаной с ординатами Y*o, Y*1, Y*2, …, Y*k+1 (синие прямоугольники). Если ΔХ мало - можно полагать, что уравнение касательной к искомой функции в точке Хо (прямая YoY1*) не сильно отличается от Y(X) на участке ΔХ (дуга YoY1). Найдем Y1:
Y1*=Yo+ΔY1=Yo+ ΔХ·Tg(Ώo).
Тангенс Ώo равен значению производной функции Y(X) в точке Хо, которую легко вычислить:
Tg(Ώo)=Y'o=Z(Xo,Yo)
И можем записать Y*=Yo+ ΔХ·Z(Xo,Yo).
Следующий шаг – проведение касательной к Y(X1), т.е. построение участка с тангенсом наклона, равным Z(X1,Y1). Однако поскольку нам известно не точное значение Y1, а приближенное Y*1, проведем линию с тангенсом угла наклона, равным Z(X1,Y*1).
Тогда Y*2=Y*1+ ΔХ·Z(X*1,Y*1).
Отсюда можем получить рабочие формулы метода
Xk+1=Xk+ ΔХ
Yk+1=Yk+ ΔХ·Z(Xk,Yk).
Метод является весьма приблизительным (сравните вычисленную и настоящую функции на рисунке). Уменьшив шаг интегрирования ΔХ, можно добиться приемлемой погрешности. При ΔХ→0 решение сходится к точному.
Пример численного решения дифференциального уравнения методом Эйлера.
Представить решение дифференциального уравнения вида 
при начальных условиях Y(0)=1. Решение Y=exp(X2) такого простого уравнения известно, что позволит нам оценить точность вычислений в таблице. Здесь в ячейке В1 установлен шаг интегрирования 0,04, в В4 и С4 – начальные условия уравнения. Текущие значения Х вычисляются по формулам. В столбце Yэ находится решение по методу Эйлера, в столбце Yт – точное решение с непосредственным использованием функции exp(X2). Решение доведено до 1,96 (50 шагов).
Рис.1 Рис.2
По графику видно (рис.1), что точное решение и решение, полученное с помощью метода Эйлера, достаточно близки. (График с маркерами, помечающими точки данных). Дальнейшее снижение погрешности может быть достигнуто уменьшением шага интегрирования и увеличением предела интегрирования. Например, при изменении шага в 2 раза получаем график, изображенный на рис.2.
Конечно, при такой организации вычислительных процессов, к которой нам пришлось прибегнуть для интегрирования и решения дифференциальных уравнений, мы ограничены числом строк (65536) в рабочем листе Excel. И хотя мы можем продолжить вычисления на другом листе, нам вряд ли понадобится такое количество строк.
Как было сказано выше, метод Эйлера является самым простым (и самым грубым) средством решения дифференциальных уравнений. Можно воспользоваться и более точными методами, например, методом Рунге-Кутта.