Постулаты квантовой механики. Операторы.

Министерство образования Украины

НТУУ “КПИ”

 

Решение типичных задач в курсе квантовой механики

Часть 1

Киев 2002

Рецензенты

Д-р ф.-м. наук Олейник В.П.

Канд. ф.-м. наук Гусева О.А.

Терентьева Ю.Г.

 

Решение типичных задач в курсе квантовой механики.

НТУУ «КПИ» 2002

 

 

Содержание

Введение………………………………………………………………………...3

Часть 1. Постулаты квантовой механики. Операторы.……………………....4

Уравнение Шредингера……..……………………...…….…..……..8

Соотношение неопределенностей. …………….……………………

Раздел 2. Типичные задачи.

Частица в одномерной прямоугольной потенциальной яме с

бесконечными стенками. …..…………………….…………….…12

Частица в сферической потенциальной яме……………………...22

Туннельный эффект………………………………………………..27

Самостоятельная расчетная работа «Определение коэффици-

ента туннелирования частицы через потенциальный барьер»….31

Введение.

В процессе изучения общего курса физики студентам технических специальностей приходится относительно поверхностно знакомиться с общими положениями, особенностями и математическим аппаратом квантовой физики. Учитывая стремительное развитие электроники, четко выраженную направленность технологий на микромизацию размеров электронных элементов и, как следствие, выход за рамки описания с помощью только классических представлений о строении вещества, возрастает потребность в более глубоком и основательном изучении студентами квантовых процессов. Поэтому для качественного усвоения методов квантовой механики на начальном этапе очень большое значение имеет грамотный и всесторонний анализ простейших задач. Он, во-первых, позволяет студенту легче перестроиться на "язык" квантовой механики и оторваться от таких привычных понятий, как "точный момент времени", "точное местоположение частицы", приучая оперировать новым понятием "функция состояния", а во-вторых, дает возможность студенту сориентироваться в случае более сложных систем.

Поскольку основой для решения практически любой квантовомеханической задачи является уравнение Шредингера, от студентов требуется глубокое понимание физического содержания этого уравнения. Поэтому в пособии приведено его обоснование и анализ.

Цель данного методического пособия состоит, в частности, и в том, чтобы максимально подробно и всесторонне изучить некоторые типичные квантовомеханические задачи, которые включены в курс общей физики и обязательны для понимания. Кроме того, рассмотрены вопросы, связанные с новым для студентов понятием квантования энергии частицы.

В пособии проведен подробный анализ поведения частицы в случае двух наиболее простых моделей потенциальных полей - прямоугольного одномерного и сферически-симметричного. В качестве основы использованы задачи из базового задачника И. Е. Иродова "Задачи по общей физике" (раздел 6.2 - волновые свойства частиц), а также "Сборника задач по общему курсу физики" под редакцией Д. В. Сивухина (раздел "Атомная физика, физика ядра и элементарных частиц").

Наконец, в данном пособии проведен анализ поведения частицы при прохождении ее через потенциальный барьер. Необходимость такого анализа продиктована тем, что базовые учебники, как правило, содержат лишь математическое описание туннельного эффекта, мало останавливаясь на физической сути, что приводит к сложностям в понимании студентами одного из наиболее ярких проявлений квантовой природы вещества.

Раздел 1

 

Постулаты квантовой механики. Операторы.

 

Микромир для нас непосредственно не наблюдаем. О движении микрочастиц можно судить лишь по тем макроскопическим эффектам, которые они вызывают. Наукой, описывающей поведение микрочастиц, является квантовая механика. Как и любая научная дисциплина, квантовая механика имеет свои постулаты. Следствия, вытекающие из постулатов квантовой механики, многократно подтверждены экспериментально, и это является подтверждением их правильности. Рассмотрим постулаты квантовой механики.

1. Вся информация о физической системе содержится в функции состояния. Функцию состояния называют также волновой функцией и обозначают через Y. Под физической системой понимают то, что подлежит изучению: электрон, нуклон, фотон и т.п. или любую их комбинацию. В результате изучения физической системы получают набор действительных чисел: значения координат, импульса, энергии и т.п. В квантовой механике предполагается, что информация об этих числах, то есть о поведении физической системы, содержится в волновой функции Y. О явном виде функции состояния изначально известно только, что она каким-то образом зависит от координат частиц, составляющих систему, и от времени. Для одной частицы

Y=Y(x,y,z,t), (1)

где x,y,z – декартовы координаты, t- время. Произведение dx^.dy^.dz=dV называется элементарным объемом. На Y-функцию накладываются следующие ограничения: она должна быть в своей области определения непрерывной, однозначной и квадратично интегрируемой. Эти требования являются органичными следствиями того, что квадрат волновой функции есть плотность вероятности нахождения частицы в бесконечно малой окрестности некоторой точки с координатами (x, y, z), а вероятность не может иметь разрывов, не может иметь несколько значений при одном и том же наборе аргументов и вычисляется путем интегрирования плотности вероятности по объему всего пространства. Задача состоит в том, чтобы извлечь требуемую информацию из функции состояния Y. Способ извлечения информации из Y-функции устанавливается следующими постулатами.

2. Каждой физической величине (энергии, импульсу и т.д.) ставится в соответствие определенный оператор. - ОПЕРАТОР - Под оператором понимают действие, производимое над некоторой функцией. Этим действием может быть любое математическое действие – умножение на число, извлечение корня, дифференцирование, интегрирование и т.д.

- ЛИНЕЙНЫЙ ОПЕРАТОР - В квантовой механике используются только линейные операторы, то есть такие, которые подчиняются правилу

(2)

где С ₁ и С ₂ – произвольные постоянные, а f ₁ и f ₂ – произвольные функции. Простейшим примером такого оператора может служить наиболее часто используемый в квантовой механике оператор дифференцирования. Действительно, производная от суммы функций есть сумма производных этих функций. А вот, например, оператор извлечения корня не является линейным.

В квантовой механике каждой физической величине ставится в соответствие линейный оператор. Основными являются следующие операторы:

- оператор координаты, который есть умножение на саму координату:

(4)

- оператор импульса.

Импульс – вектор. Обозначим проекции импульса на оси координат через p_x, p_y, p_z. Этим составляющим соответствуют следующие

- операторы проекции импульса

(5)

где , h = 1,05^.10^-34 Дж^.с – постоянная Планка.

Оператор полного импульса является вектором, как и сам импульс. Если обозначить единичные вектора вдоль декартовых осей через e _x, e _y, e _z, тогда вектор импульса равен р = e _x p_x + e _y p_y + e _z p_z Тогда

- оператор полного импульса

(6)

- оператор энергии

Ввиду исключительной важности линейных операторов для квантовой механики остановимся на их свойствах подробнее. Пусть имеется линейный оператор . Подберем такую функцию Y _n, чтобы результат действия на нее оператора сводился к умножению функции Y _n на постоянный множитель l _n, чтобы выполнялось соотношение . В этом случае Y _n – собственная функция оператора , а число l _n – собственное значение, соответствующее этой собственной функции. Обычно у оператора существует несколько (а в квантовой механике – бесконечно много) собственных функций и собственных значений. В общем случае собственные значения могут быть любыми – и комплексными, и вещественными. В квантовой механике рассматриваются лишь такие операторы, собственные числа которых вещественны. Это и понятно, поскольку физическое содержание собственных чисел – это те самые значения физической величины (соответствующей данному оператору), которые можно измерить экспериментально. Например, если в результате действия оператора импульса на волновую функцию состояния, скажем, электрона, получим собственное число р, то это число и есть значение импульса этого электрона в этом состоянии. Достоинство квантовой механики состоит в том, что абстрактные, казалось бы, действия операторов с абстрактной волновой функцией позволяют получить набор чисел, которые могут быть измерены и проверены экспериментально.

Далее, любая физическая величина, которая может быть измерена экспериментально, является вещественной. В связи с этим – следующий постулат:

3. Единственно возможными значениями физической величины являются собственные значения ее оператора. В классической механике физические величины могут принимать любые значения. Например, энергия колеблющейся частицы E=mv²/2+kx²/2 может быть любой в зависимости от величины скорости v и координаты x. В квантовой механике дело обстоит иначе. Третий постулат утверждает, что для определения возможных значений физической величины надо найти собственные значения l _n уравнения , где - оператор, соответствующий интересующей нас физической величине, а Y- функция состояния. Этот постулат дает способ построения уравнений квантовой механики и решения наиболее важной задачи – определения возможных значений физической величины. Чтобы определить, какие значения может принимать данная физическая величина, необходимо составить для нее уравнение классической механики (уравнение сохранения), заменить величины, входящие в уравнение классической механики соответствующими операторами и найти собственные значения полученного оператора.

4. Поскольку волновая функция является функцией принципиально комплексной, то согласно правилам ТФКП (теории функции комплексной переменной) квадрат ее модуля определяется, как

, (7)

где через ψ* обозначают функцию комплексно сопряженную к ψ. А постулат звучит так:

Квадрат модуля функции состояния есть плотность вероятности того, что частица находится внутри малого объема dV=dx^.dy^.dz^. в окрестности точки (x,y,z). Например, в одномерном случае (когда ) вероятность нахождения частицы в интервале (х₁,х₂) вычисляется, как

(8)

Если точно известно, что некая частица в пространстве существует, то вероятность того, что она находится внутри этого пространства, равна единице, тогда

(9)

Последнее равенство является условием нормировки волновой функции. Следует подчеркнуть, что сама волновая функция физического смысла не имеет, это «всего лишь» функция, правда, содержащая в себе всю возможную физическую информацию о частице.

 

Таким образом, в соответствии с изложенными выше положениями квантовой механики, состояние микрочастицы или системы микрочастиц носит вероятностный характер и описывается вероятностными законами. В классической статистической физике при описании системы, состоящей из многих частиц, также используются вероятностные законы. Имеется, однако, принципиальное различие между вероятностными предсказаниями классической статистической физики и квантовой механики. В статфизике вероятностные распределения являются результатом взаимодействия большого числа частиц, поведение же каждой отдельной частицы подчиняется законам классической механики. В квантовой механике поведение даже одной частицы описывается вероятностными законами.

 

Уравнение Шредингера

Центральной задачей квантовой механики является задача о нахождении энергии частицы, движущейся в поле с заданной потенциальной энергией U. Следуя третьему постулату, очевидно, следует записать классический закон сохранения энергии,

(10)

а затем заменить физические величины соответствующими им операторами. Итак, классический импульс заменим оператором импульса, действующим на волновую функцию частицы,

(11)

потенциальную энергию – оператором потенциальной энергии, действующим на волновую функцию,

(12)

а полную энергию частицы - оператором полной энергии, действующим на все ту же волновую функцию частицы

(13)

Теперь подставим все замены в классическое уравнение закона сохранения энергии и получим

 

(14)

Это и есть нестационарное уравнение Шредингера.

В каждом конкретном случае, для каждого конкретного потенциала, аналитический вид которого задается в условии задачи, можно попытаться решить это уравнение и найти волновую функцю частицы.

Известно (см., например, Савельев т.3), что волновую функцию свободной частицы можно представить в виде

(15)

Тогда, подставив волновую функцию в нестационарное уравнение, после сокращения экспонент получим так называемое стационарное уравнение Шредингера

 

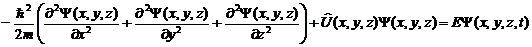(16)

В результате его решения можно определить не только вид волновой функции частицы в конкретном потенциале, но и возможные значения энергии частицы. Стационарное решение другими словами означает «неизменное во времени распределение вероятности нахождения частицы в пространстве» – где-то в пространстве вероятность найти частицу большая, где-то эта вероятность наиболее велика, где-то равна нулю.

Попутно в ходе решения этого уравнения определяется набор чисел Е_n – возможных значений энергии, который называется энергетическим спектром частицы. Как уже отмечалось выше, энергетический спектр может быть и сплошным, например, в случае свободного движения частицы В классической статистической физике при описании системы, состоящей из многих частиц, также используются вероятностные законы., и дискретным – в случае, если на свободное движение частицы накладываются ограничения в виде внешнего потенциального поля.