Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
16. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом 2a (рис.8.7.).
Для определения положения центра тяжести кругового сектора разобьем его на элементарные сектора. Каждый элементарный сектор можно рассматривать как равнобедренный треугольник с высотой равной R. Эта высота является также и медианой.
следовательно, центр тяжести каждого треугольника лежит на расстоянии 
R от начала координат О.
Следовательно, центр тяжести сектора совпадает с центром тяжести дуги DE. Тогда окончательно получим, что центр тяжести кругового сектора лежит на оси симметрии на расстоянии от центра
ХC= R 
.
18. Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом 
. В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).
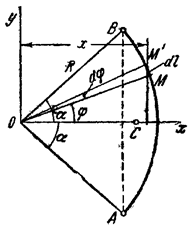
Рис.10
Найдем координату 
по формуле 
. Для этого выделим на дуге АВ элемент ММ’ длиною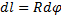 
, положение которого определяется углом 
. Координата х элемента ММ’ будет 
. Подставляя эти значения х и d l и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
где L - длина дуги АВ, равная 
.
Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном 
где угол 
измеряется в радианах.
19. Векторный способ задания движения точки
В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией r=r(t)
Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):
V=dr/dt (1.2)
Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.
А
б
Рисунок 1.2
Ускорение точки (изменение ее скорости) определяется как производная от скорости:
Вектор ускорения направлен по касательной к годографу вектора скорости (рисунок 1.2, б).
20. В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:
x =x(t) y=y(t) z=z(t)
Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.
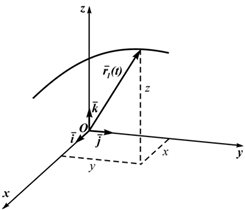
Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):
r(t)=i⋅x(t) + j ⋅y(t) + k⋅z(t) (1.5)
Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:
То есть:
Направление вектора скорости определяется с помощью направляющих косинусов:
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.
Аналогичны формулы для определения ускорения точки:
Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат
22. Ускорение точки., [м/сек2]. Проекции уск.-я: и т.д. Модуль уск.-я:, направляющ. косинусы:, и т.д.
При задании движения в полярных координатах: проекции ускорения на радиальное направление, поперечное направление, модуль ускорения. При естественным сп. задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:. Модуль нормального ускорения:, r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения, направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движ-ии направление касат. уск. и скорости совпадают, при замедленном – противоположно. ^, Þ. Вектор ускорения лежит в соприкасающейся плоскости Þ его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль – ^ к главной нормали и касательной).
23. Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.
Теорема. При поступательном движении твердого тела все его точки движутся по одинаковым и параллельным траекториям и имеют в каждый данный момент времени равные по модулю и направлению скорости и ускорения.
Доказательство. Для доказательства теоремы рассмотрим движение отрезка прямой,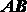 
проведенного в теле, совершающем поступательное движение (рис. 2.10). Из определения поступательного движения следует, что в каждый данный момент времени отрезок, 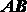занимающий последовательно положения 
, 
, 
и т.д., остается параллельным своему первоначальному положению. Учитывая это и то что, 
делаем вывод, что ломаные линии 
и 
параллельны и при наложении совпадут всеми своими точками. При бесконечном уменьшении промежутков времени между рассматриваемыми положениями отрезка мы видим, что точка 
и точка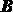 
описывают одинаковые кривые, т. е. кривые, совпадающие при наложении.
Для доказательства второй части теоремы заметим, что
Возьмем производные по времени от левой и правой частей
Так как, 
то. 
Тогда
Разобранная теорема позволяет сделать вывод, что поступательное движение твердого тела вполне определяется движением какой-либо одной его точки.
24. Враща́тельное движе́ние — вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Осьвращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения роторагенератора на электростанции неподвижна.
Кинематические характеристики
Вращение характеризуется углом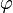 
, измеряющимся в градусах или радианах, угловой скоростью 
(измеряется в рад/с) и угловым ускорением 
(единица измерения — рад/с²).
25. Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.
Скорость точки тела.
Вектор скорости можно получить векторным произведением:
V=ω⊗ r, V=ω⋅rsinα=ωR.
Скорость точки является положительной величиной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.
Ускорение точки тела
Ускорение при естественном способе задания движения определяется как сумма касательного и нормального ускорений.
26. Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же неподвижной плоскости.
Её обобщенные координаты – две координаты 
полюса С (рис. 6,а) и угол 
поворота фигуры вокруг полюса (вокруг оси Cz, проходящей через полюс и перпендикулярной плоскости движения).
Движение плоской фигуры можно рассматривать как сложное движение тела, являющимся результатом сложения поступательного движения плоской фигуры вместе с полюсом С и её вращательного движения вокруг полюса С.
Поступательное движение фигуры вместе с полюсом рассматривается как переносное, вращательное вокруг полюса – как относительное её движение.
а б в
Рис. 6. Плоская фигура. Скорость и ускорение точки 
28. Мгновенным центром скоростей (МЦС) называется такая точка плоской фигуры, скорость которой в данный момент времени равна нулю.
При любом непоступательном движении плоской фигуры такая точка всегда существует. Действительно,
Пусть в данный момент времени известно положение МЦС фигуры. Тогда, принимая его за полюс и учитывая, что 
, получим по формуле (4) для произвольной точки фигуры
т.е. знание МЦС упрощает определение скоростей точек плоской фигуры, т.к. сразу позволяет определить модуль скорости по формуле (5) и направление: 
.
Таким образом, при известном МЦС вектор скорости любой точки плоской фигуры равен
модуль определяется по формуле
30. Сложное движение точки (тела) – такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O1x1y1z1).
29. Покажем, что ускорение любой точки М тела при плоском или параллельном движении(так же как и скорость) складывается из ускорений, которые она получает в поступательном и во вращательном движении.
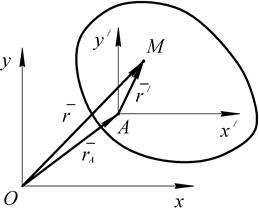
Положение точки М по отношению с осями 0ху определяется радиусом–вектором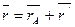 
, где 
. Тогда
. В полученном равенстве 
– равна ускорению полюса А, а величина 
– определяет ускорение, полученное точкой М при ее вращении вместе с телом вокруг полюса А.
Следовательно 
.
При этом для ускорения 
во вращательном движении вокруг полюса по формулам будет
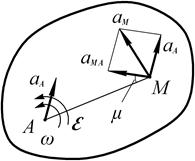
- угловая скорость и угловое ускорение, 
- угол между направляющей и отрезком МА.
31. Теорема: абсолютная скорость точки равна векторной сумме относительной и переносной скоростей.
Пусть за время Δt точка переместилась из положения А в положение А3, двигаясь по траектории абсолютного движения, т. е. по дуге АА3 (см. рис. 1).
Если бы имело место только относительное движение, то точка перешла бы в положение А2. Можно представить, что точка А перешла в положение А3, двигаясь сначала только по траектории переносного движения (дуга АА2), а затем только по траектории относительного движения (дуга А2А3 равная дуге АА1).
Соединив точки А, А2 и А3 хордами, получим следующую зависимость между векторами перемещений точки А:
АА3 = АА2 + А2А3.
Разделим все члены равенства на Δt и перейдем к пределу при Δt, стремящемся к нулю:
lim (AA3)/Δt = lim (AA2)/Δt + lim (A2A3)/Δt, что дает v = ve + vr,
где: v – вектор абсолютной скорости; ve - вектор переносной скорости; vr – вектор относительной скорости.
Теорема доказана.