Найдём вторую производную:
 ;
;
Найдём значение второй производной в критических точках.
 .
.
 .
.
Значит, прибыль в точке  максимальная.
максимальная.
Найдём значение максимальной прибыли:
 .ƒ
.ƒ
3.9. Требуется изготовить коническую воронку с образующей, равной 15 см. Какова должна быть высота воронки, чтобы её объём был наибольшим?
n Пусть  , тогда:
, тогда:
 .
.
Объём:
 .
.
 ;
;
Найдём критические точки функции:
 ;
;
 ;
;
 ;
;
 .
.
Получили, чтобы объём воронки с образующей 15 см был наибольшим, высота её должна быть равной  см. ƒ
см. ƒ
Выпуклость функции и точки перегиба.
Достаточные условия выпуклости.
Пусть  существует на отрезке
существует на отрезке  , а
, а  — на интервале
— на интервале 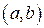 . Тогда:
. Тогда:
1) если
 при всех
при всех  ,
,
то функция  выпукла вниз на отрезке
выпукла вниз на отрезке  .
.
2) если
 при всех
при всех  ,
,
то функция  выпукла вверх на отрезке
выпукла вверх на отрезке  .
.
Необходимое условие наличия точки перегиба.
Если  — точка перегиба функции
— точка перегиба функции  и если функция
и если функция  имеет в некоторой окрестности точки
имеет в некоторой окрестности точки  вторую производную, непрерывную в точке
вторую производную, непрерывную в точке  , то
, то
 .
.
Достаточные условия наличия точки перегиба.
1) Если функция  непрерывна в точке
непрерывна в точке  , имеет в этой точке конечную или бесконечную производную и если функция
, имеет в этой точке конечную или бесконечную производную и если функция  меняет знак при переходе через точку
меняет знак при переходе через точку  , то
, то  — точка перегиба функции
— точка перегиба функции  .
.
2) Если  ,
,  , то
, то  — точка перегиба функции
— точка перегиба функции  .
.
Примеры
4.1. Показать, что функции  выпукла вверх на всей области определения.
выпукла вверх на всей области определения.
n Вычислим вторую производную
 .
.
Область определения функции

множество  . Очевидно,
. Очевидно,  для любых
для любых  .ƒ
.ƒ
4.2. Найти точки перегиба линии  ,
,  .
.
n Вычислим вторую производную параметрически заданной функции оп формуле
 .
.
Так как  ,
,  ,
,  ,
,  , получаем
, получаем
 .
.
Разобьем ось  точками
точками  ,
,  ,
,  на три интервала. На каждом из этих интервалов вторая производная
на три интервала. На каждом из этих интервалов вторая производная  сохраняет знак. Составим таблицу значений
сохраняет знак. Составим таблицу значений  ,
,  и знака
и знака  на соответствующих интервалах.
на соответствующих интервалах.

| 
| 
| 
|

| 
| 
| 
|

| 
| 
| 
|

| От  до до 
| 
| 
|

| 
| 
| 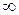
|

| 
| 
| 
|

| 
| 
| 
|

| 
| 
| 
|
Таким образом, точками перегиба будут  и
и  .ƒ
.ƒ
4.3. Найти точки перегиба и интервалы выпуклости функции 
n Вычисляя производные
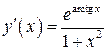 ,
,  .
.
Составим таблицу постоянства знаков второй производной.

| 
| 
|

| 
| Выпукла вниз |

| 
|  Точка перегиба
Точка перегиба
|

| 
| Выпукла вверх |
Таким образом, точка  - точка перегиба.ƒ
- точка перегиба.ƒ
4.4. Найти точки перегиба линии  ,
,  .
.
n Вычислим вторую производную, параметрически заданной функции по формуле
 .
.
Так как  ,
,  ,
, 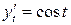 ,
,  , получаем
, получаем
 .
.
Точки, в которых 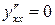 определяются из уравнения
определяются из уравнения  , и нетрудно убедиться, что в
, и нетрудно убедиться, что в  ,
,  , вторая производная меняет знак, следовательно, эти точки – точки перегиба.ƒ
, вторая производная меняет знак, следовательно, эти точки – точки перегиба.ƒ
4.5. Показать, что точки перегиба линии  лежат на линии
лежат на линии  .
.
n Точки пересечения линий удовлетворяют уравнению
 . (*)
. (*)
Покажем, что точки перегиба линии  удовлетворяют этому уравнению. Вычисляя вторую производную и приравнивая ее нулю получаем уравнение
удовлетворяют этому уравнению. Вычисляя вторую производную и приравнивая ее нулю получаем уравнение
 или
или  , (**)
, (**)
так как  . Подставляя (**) в (*) получаем тождество
. Подставляя (**) в (*) получаем тождество
 .ƒ
.ƒ
Асимптоты.
Вертикальная асимптота.
Если выполнено хотя бы одно из условий
 ,
,  ,
,
то прямую  называют вертикальной асимптотой графика функции
называют вертикальной асимптотой графика функции  .
.
Невертикальная асимптота.
Прямую

называют невертикальной асимптотой графика функции  при
при  , если
, если
 .
.
Если  , то асимптоту называют наклонной, а если
, то асимптоту называют наклонной, а если  , то асимптоту
, то асимптоту  называют горизонтальной.
называют горизонтальной.
Аналогично вводится понятие асимптоты при  .
.
Для того чтобы прямая  была асимптотой графика функции
была асимптотой графика функции  при
при  , необходимо и достаточно, чтобы существовали конечные пределы
, необходимо и достаточно, чтобы существовали конечные пределы
 ,
,
 .
.
Аналогично находится асимптота при  .
.
Исследование асимптот при  и при
и при  как правило проводят отдельно.
как правило проводят отдельно.
В некоторых частных случаях возможно совместное исследование асимптот при  и при
и при  , например, для
, например, для
1) рациональных функций;
2) четных и нечетных функций, для графиков которых исследование можно проводить на части области определения.
Следует отметить, что метод вычисления пределов для нахождения асимптот не позволяет оценить взаимное расположение графика функции и его асимптоты. Для определения взаимного положения графика и асимптоты можно пользоваться следующими правилами.
1) Если функция 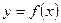 имеет асимптоту при
имеет асимптоту при  , дифференцируема и строго выпукла вниз на луче
, дифференцируема и строго выпукла вниз на луче  , то график функции лежит выше асимптоты.
, то график функции лежит выше асимптоты.
2) Если функция 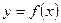 имеет асимптоту при
имеет асимптоту при  , дифференцируема и строго выпукла вверх на луче
, дифференцируема и строго выпукла вверх на луче  , то график функции лежит ниже асимптоты.
, то график функции лежит ниже асимптоты.
3) Могут быть другие случаи поведения графика функции при стремлении к асимптоте. Например, возможно, что, график функции бесконечное число раз пересекает асимптоту.
Аналогичное утверждение справедливо и при  .
.
До исследования свойств выпуклости графика функции взаимное расположения графика функции и его асимптоты можно определить по знаку  в методе выделения главной части.
в методе выделения главной части.
Метод выделения главной части. Для нахождения асимптоты выделяем главную часть функции при  . Аналогично при
. Аналогично при  .
.
Главную часть дробно рациональной функции удобно находить, выделяя целую часть дроби.
Главную часть иррациональной функции при решении практических примеров удобно находить используя методы представления функции формулой Тейлора при  .
.
Главную часть иррациональных функций вида  и
и  удобно находить соответственно методом выделения полного квадрата или полного куба подкоренного выражения.
удобно находить соответственно методом выделения полного квадрата или полного куба подкоренного выражения.
Примеры
5.1. Найти асимптоты графика функции
 .
.
n Прямая  — вертикальная асимптота.
— вертикальная асимптота.
Наклонная асимптота. Найдем угловой коэффициент  и свободный член
и свободный член  по формулам
по формулам
 ,
,


Таким образом, прямая  — наклонная асимптота.
— наклонная асимптота.
Найдем асимптоту методом выделения главной части дробно-рациональной функции. Выполняя деление «столбиком», получаем

То есть,  .
.
Таким образом, прямая  — наклонная асимптота.ƒ
— наклонная асимптота.ƒ
5.2. Найти асимптоты линии:  .
.
n Вертикальных и горизонтальных асимптот нет.
Выражая уравнение линии в явном виде:  .
.
Тогда
 ,
,
 .
.
В итоге имеем 2 наклонных асимптоты:  .ƒ
.ƒ
5.3. Найти асимптоты линии:  .
.
n Выразим уравнение линии в явном виде:  .
.
Так как 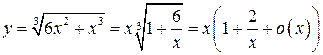 ,
,
то прямая  - наклонная асимптота.ƒ
- наклонная асимптота.ƒ
5.4. Найти асимптоты функции: 
nТак как функция не определена в точках  =
=  1, то
1, то  - вертикальные асимптоты.
- вертикальные асимптоты.
Найдём наклонную асимптоту: угловой коэффициент прямой  и число
и число  найдём, применяя формулы:
найдём, применяя формулы:
 ;
;  .
.
 .
.
Получили: 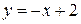 - наклонная асимптота. ƒ
- наклонная асимптота. ƒ
5.5. Найти наклонную асимптоту графика функции  .
.
n Так как
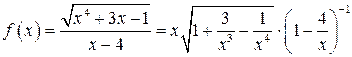 ,
,
то по формуле Тейлора получаем

и прямая  является искомой асимптотой. ◄
является искомой асимптотой. ◄
5.6. Найти наклонные асимптоты графика функции  при
при  и
и 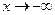 .
.
n В подкоренном выражении выделим полный квадрат
 .
.
Так как график функции 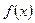 симметричен относительно прямой
симметричен относительно прямой  и
и

то  при
при  . Значит, прямая
. Значит, прямая  является асимптотой при
является асимптотой при  , а прямая
, а прямая  — асимптотой при
— асимптотой при 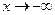 . ◄
. ◄