Пусть по выборке (xi, yi) требуется определить оценки коэффициентов b 0 и b 1 эмпирического уравнения регрессии (5.8). В случае использования МНК минимизируется следующая функция потерь:
. (10)
Нетрудно заметить, что функция Q является квадратичной функцией двух параметров b 0 и b 1, поскольку xi и yi – известные данные наблюдений. Поскольку функция Q непрерывна, выпукла и ограничена снизу (Q ³0), то она имеет минимум.
Необходимым условием существования минимума функции двух переменных (10) является равенство нулю ее частных производных по неизвестным параметрам b 0 и b 1:
(11)
После преобразований получим систему нормальных уравнений (систему линейных алгебраических уравнений) для определения параметров простой линейной регрессии:
(12)
Разделив оба уравнения на n, получим:
(13)
Здесь 
, 
, 
, 
. Таким образом, оценки параметров простой линейной регрессии по МНК определяются по формулам (13).
Нетрудно заметить, что b 1 можно вычислить по формуле
, (14)
где rxy – выборочный коэффициент корреляции, 
и 
– средние квадратичные отклонения.
Таким образом, коэффициент регрессии b 1 пропорционален коэффициенту корреляции. Следовательно, если коэффициент корреляции rxy уже рассчитан, то легко может быть найден коэффициент регрессии b 1 по формуле (14).
Отметим, что кроме уравнения регрессии Y на X: 
,
для тех же эмпирических данных может быть найдено уравнение регрессии X на Y: 
.
Коэффициенты регрессии bx и by в этом случае будут связаны равенством:
. (15)
Подставляя значения b 0 и b 1, вычисленные по формулам (13), в (8), получим уравнение линейной регрессии Y на X:
. (16)
Аналогично можно получить уравнение линейной регрессии X на Y:
. (17)
Можно заметить, что обе прямые регрессии пересекаются в точке 
. Причем, чем больше коэффициент корреляции, тем меньше угол φ между прямыми (рис. 2).
В частности, если r =±1, то обе прямые регрессии совпадут. Если коэффициент корреляции равен нулю, то линии регрессии будут параллельны координатным осям.
Рис. 2
Полученные формулы для коэффициентов регрессии позволяют сделать ряд выводов:
1. Эмпирическая прямая регрессии обязательно проходит через точку 
.
2. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений 
, а также среднее значение отклонений 
равны нулю.
% Действительно, из формулы 
в соотношении (11) следует, что 
.
3. Случайные отклонения ei не коррелированы с наблюдаемыми значениями yi зависимой переменной Y.
Для обоснования данного утверждения покажем, что ковариация между Y и e равна нулю. Действительно,
.
Покажем, что 
. Просуммировав по i все соотношения (9), получим:
,
т.к. 
. Разделив последнее соотношение на n, получим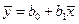 
. Вычитая из (5.9) полученное соотношение, приходим к следующей формуле:
. (5.18)
Тогда
.
Следовательно, 
. &
4. Случайные отклонения ei не коррелированы с наблюдаемыми значениями xi независимой переменной X.
% Действительно, 
в силу второй формулы системы (5.11). &
Для иллюстрации МНК рассмотрим следующий пример,