ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Сопротивление бруса разным видам деформации зависит не только от его материала и размеров, но и от формы его поперечных сечений.
Форма поперечного сечения учитывается в таких геометрических характеристиках:
- статические моменты площади Sz, Sy;
- моменты инерции Iz, Iy, Izy, Ir;
- моменты сопротивления Wz, Wy, Wr.
Статические моменты площади
Рассмотрим произвольную плоскую фигуру (поперечное сечение бруса). Малый элемент площади dA в системе координат zOy имеет координаты z и y (рис. 13).
Статический момент 
площади А относительно оси Oz -это геометрическая характеристика, которая определяется интегралом
где у - расстояние от элементарной площадки dA до оси Oz.
Рис.13
Аналогично вычисляется статический момент 
площади A относительно оси у:
где z - расстояние от площадки dA до оси Oy.
В зависимости от расположения осей Oz и Oy статические моменты и могут быть положительными, отрицательными или равняться нулю. Размерность и - [ м3 ], [ см3 ].
Если величины и известны, то координаты центра тяжести zc, yc сечения (рис. 13) определяются по формулам
; 
.
Если величины zc, yc известны, то статические моменты площади A определяются по таким формулам:
; 
,
где zc, yc - расстояния от центра тяжести до осей Oz, Oy соответственно.
Из последних формул видно, что статические моменты площади относительно центральных осей (осей, которые проходят через центр тяжести) равняются нулю.
Рассмотрим пример (рис. 14). Определить: а) статический момент треугольника относительно оси, которая проходит через его основание, б) расстояние от основания до центра тяжести треугольника.
По определению
где 
- площадь элементарной площадки;
b(y) -ширина треугольника на расстоянии у от оси Oz определяется из соотношения сторон подобных треугольников:
Рис. 14
, 
.
Отсюда
;
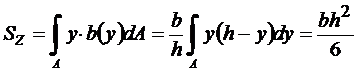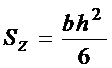
Следовательно, если статический момент известен, тогда
; 
Для определения статических моментов сложной фигуры ее разбивают на простые части (рис. 15), для каждой из которых известны площади Ai и координаты центров тяжести zci и yci.
Статический момент площади всей фигуры определяется как сумма статических моментов для каждой части:
,
.
Рис. 15
Координаты центра тяжести zc и yc всей фигуры определяем по таким формулам:
; 
.
В общем случае координаты центра тяжести сечения сложной формы вычисляются так:
; 
,
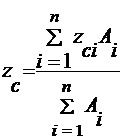где Ai - площади простых частей сечения; n - количество простых частей, из которых состоит сечение; zci и yci - координаты их центров тяжести в некоторой общей для всех частей системе координат zOy.
Моменты инерции плоских фигур
Осевые моменты инерции сечения - это геометрические характеристики, которые определяются интегралами
где dA - площадь элементарной площадки; y, z - расстояния от dA (рис. 16) до осей Oz и Oy соответственно.
Рис.16
Полярный момент инерции плоской фигуры относительно данной точки (полюса 0) - это геометрическая характеристика, определяемая інтегралом вида
,
где r - радиус-вектор центра тяжести элементарной площадки dA.
Осевые и полярные моменты инерции могут иметь лишь положительные значения.
Если через полюс проведена система прямоугольных координатных осей z и y, то
,
тогда
.
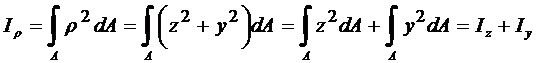Следовательно, полярный момент инерции равняется сумме осевых.
Центробежный момент инерции вычисляется по формуле
и в зависимости от положения осей может быть положительным, отрицательным или равняться нулю.
Вращая оси, можно найти такое их положение, при котором 
= 0. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции. Главные оси, которые проходят через центр тяжести сечения, называются главными центральными осями инерции.
Если сечение имеет ось симметрии, то эта ось является одной из главных центральных осей, другая - располагается перпендикулярно к первой и проходит через центр тяжести сечения.
Размерность 
, 
, 
, 
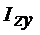- [ м4 ], [ см4 ].
Пример 1:
Определить момент инерции прямоугольника относительно центральных осей y, z, параллельных его сторонам (рис. 17).
Рис.17
По определению
Для прямоугольника 
; 
.
Пример 2: Определить момент инерции треугольника относительно оси, проходящей через его основание (рис. 14).
Выделим элементарную площадку, параллельную указанной оси,
,
где b(y) - ширина треугольника на расстоянии y от оси Oz.
Рассматривая подобные треугольники, имеем такие соотношения между их сторонами:
; 
.
Момент инерции по определению
;
Для треугольника .
Пример 3: Определить момент инерции круга относительно его центра и центральных осей (рис. 18).
Выделим элементарную площадку в виде бесконечно тонкого кольца с радиусом r и толщиной dr. Площадь такого элемента
Полярный момент инерции по определению
Рис. 18
Известно, что 
. Относительно круга в результате симметрии
Следовательно для круга 
При определении моментов инерции сложных сечений (рис. 15) последние можно разбить на простые части, моменты инерции которых известны. Момент инерции сложной фигуры равняется сумме моментов инерции ее составляющих частей, то есть
.
Если в сечении есть отверстие, его считают частью фигуры с отрицательной площадью.
Моменты инерции относительно параллельных осей
Пусть известны моменты инерции относительно центральных осей z 1, y 1, а именно
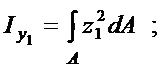
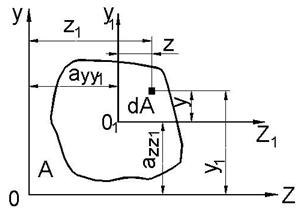Необходимо определить моменты инерции относительно осей z, y, которые параллельны центральным (рис. 19).
|
; 
,
где 
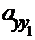- расстояния между осями z, z 1, y и y 1, соответственно, или координаты начала координат z 1 Oy 1 точки O1, в системе координат z O y.
Подчеркнем, что координаты 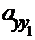во всех формулах нужно подставлять, учитывая их знаки.
Момент инерции Iz по определению
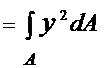
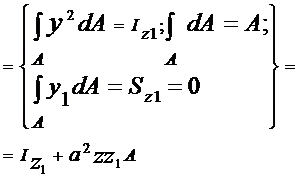
Статический момент 
равняется нулю, поскольку он вычисляется относительно центральной оси Oz 1.
Следовательно,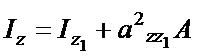 
.
Аналогично 
,
.
Момент инерции фигуры относительно произвольной оси равняется моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между этими осями.
Центробежный момент инерции относительно произвольной системы взаимно перпендикулярных осей равняется центробежному моменту инерции относительно центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.
Пример. Определить момент инерции прямоугольника относительно оси Oz, которая проходит через его сторону CD (рис. 20).
.
Из примера видим, что момент инерции сечения относительно центральной оси, всегда будет меньше, чем момент инерции относительно параллельных осей.