Достаточные признаки существования экстремума.

Чтобы исследовать поведение функции , нужно:

1) Найти ее производную

2) Приравнять эту производную к нулю и решить полученное уравнение Его корни являются стационарными точками.

3) Подвергнуть стационарные точки дополнительному исследованию, для чего нанести их на числовую ось и определить знаки на получившихся участках. Зная эти знаки, можно определить характер каждой стационарной точки . Если при прохождении через стационарную точку производная меняет знак с плюса на минус, то стационарная точка является точкой максимума. Если при прохождении через стационарную точку знак производной меняется с минуса на плюс, то стационарная точка является точкой минимума. Если при прохождении через стационарную точку производная знак не меняет, то стационарная точка не является точкой экстремума.

Иногда при нахождении экстремумов используются другие достаточные условия, в которых характер точки экстремума определяется знаком второй производной в стационарной точке.

Теорема (второе достаточное условие существования экстремума).Пусть --- стационарная точка функции 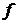(то есть и 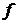имеет вторую производную , непрерывную в окрестности точки .Тогда

1)если , то --- точка максимума функции ;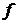

2)если , то --- точка минимума функции.

Пример 3. Найти экстремум функции .

Решение. Поскольку периодическая функция с периодом , достаточно рассмотреть лишь промежуток от 0 до . Найдем и :

, .

Приравнивая к нулю, найдем стационарные точки:

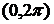или . На промежутке лежат два корня этого уравнения: и . Определим знак в этих точках: , следовательно --- точка максимума:

, следовательно --- точка минимума.

Исследование функций на выпуклость и вогнутость. Точки перегиба

Рассмотрим на плоскости кривую Г, являющуюся графиком дифференцируемой функции .

Определение 1. Кривая называется выпуклой вверх (выпуклой) на (a,b), если на этом интервале все точки кривой лежат не выше любой ее касательной.

Определение 2. Кривая называется выпуклой вниз (вогнутой) на , если на этом интервале все точки кривой лежат не ниже любой ее касательной.

Направление выпуклости кривой является важной характеристикой ее формы. Установим признаки, с помощью которых определяют интервалы, на которых график функции является выпуклым (вогнутым). Таким признаком служит, например, знак второй производной функции (если она существует).

Теорема 1. Если во всех точках интервала вторая производная функции отрицательна, то кривая на этом интервале выпукла вверх.

Теорема 2. Если во всех точках интервала вторая производная функции положительна, то кривая на этом интервале вогнута (выпукла вниз).

Пример 1. Найти интервалы выпуклости-вогнутости функции

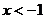
Решение. При следовательно, функция при этих выпукла; при 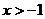, следовательно, при этих функция вогнута.

Определение 3. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны - над ней.

Теорема 3. (Необходимое условие перегиба). Если есть точка перегиба кривой и в ней существует вторая производная то .

Откуда следует, что проверять на перегиб надо лишь те точки, в которых вторая производная равна нулю или не существует.

Теорема 4. Если при переходе через точку вторая производная меняет знак, то точка кривой с абсциссой есть точка перегиба.

Пример 2.Найти точки перегиба кривой .

Решение. Область допустимых значений: .

Находим производные:

; .

Вторая производная нигде не обращается в ноль, но при не существует.

Определим знаки слева и справа от точки :

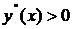при , следовательно на интервале функция вогнута;

при , следовательно на интервале функция выпукла.

Таким образом, при существует точка перегиба .

Асимптоты функций.

Определение 4. Прямая называется вертикальной асимптотой графика функции , если выполняется хотя бы одно из соотношений:

1) или 2) .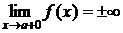

Таким образом, чтобы найти вертикальные асимптоты графика функции, надо проверять точки, в которых функция терпит разрыв, а также границы области определения.

Пример 3. Найти асимптоты кривой .

Решение. Находим точки разрыва функции: .

Находим пределы слева и справа от этой точки:

; .

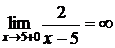Следовательно, --- вертикальная асимптота.

Определение 5. Прямая называется наклонной асимптотой графика функции , если

().

Таким образом, наличие асимптоты у графика функции означает, что расстояние от точки графика до асимптоты стремиться к нулю, когда точка 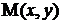удаляется в бесконечность.