ПРИМЕР 1. Найдите предел 
Решение.
Разделим числитель и знаменатель выражения на 7n. После преобразований получим:
.
(Так как при 
выражение 
стремится к нулю по свойству показательной функции с основанием 0<a<1).
ПРИМЕР 2. Найдите предел 
Решение.
Имеем неопределённость вида 
. Чтобы устранить её, разделим числитель и знаменатель на 
:
.
ПРИМЕР 3. Найдите предел 
.
Решение.
Имеем неопределённость вида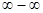 
. Чтобы раскрыть её, умножим и разделим выражение в скобках на сопряженное ему выражение 
. Получим:
.
ПРИМЕР 4. Найти предел 
Решение.
Имеем неопределенность вида “0/0”. Подвергнем функцию преобразованию, чтобы получить возможность использовать первый замечательный предел;
.
ПРИМЕР 5. Найти предел 
.
хà¥
Решение.
Имеем неопределённость вида 
. Чтобы воспользоваться вторым замечательным пределом, преобразуем данную функцию:
.
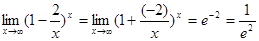ПРИМЕР 6. Продифференцировать функцию: 
.
Решение.
Находим производную данной функции по правилам дифференцирования сложной функции:
.
ПРИМЕР 7. Найти производную функции, заданной неявно: 
.
Решение.
Дифференцируем данную функцию по х:
, откуда 
ПРИМЕР 8. Найти производную 
от функции, заданной параметрически: 
.
Решение.
.
ПРИМЕР 9. Найти область определения функции 
Решение.
Данная функция определена для всех х, не обращающих в нуль знаменатель, т.е. не являющихся корнями уравнения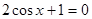 
. Это все числа вида 
.
Таким образом, область определения D(у) - вся числовая прямая, кроме точек .
ПРИМЕР 10. Исследовать функцию и построить ее график: 
Решение.
Функция определена и непрерывна в интервале (0;+¥). В граничной точке 
области определения функция имеет бесконечный разрыв, так как 
.
Так как в точке функция имеет бесконечный разрыв, то прямая является вертикальной асимптотой. Найдем уравнение наклонной асимптоты 
(если она существует).
;
.
(При нахождении пределов воспользовались правилом Лопиталя).
Итак, 
и уравнение асимптоты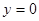 
. Таким образом, график имеет в качестве асимптот оси координат.
Найдем производную функции и критические точки:
. Стационарная критическая точка: 
. Исследуем знак производной на интервалах(0;е) и (е;¥).
Составим таблицу:
Экстремум функции: 
.
Найдем вторую производную и значения х, при которых график может иметь точку перегиба:
, 
при 
.
Определим знак второй производной в интервалах 
и 
|
|
 |
 |
Составим таблицу:
y(
)=3/(
) » 0.33
График пересекает ось абсцисс в точке (1;0). Точек пересечения с осью ординат нет. Строим эскиз графика функции:
 |
 | |||
| |||
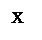
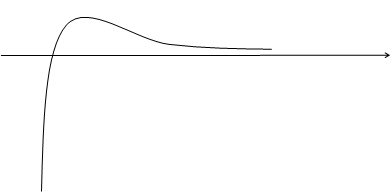ПРИМЕР 11. Построить график функции, заданной уравнением в полярных координатах
Решение.
Построим график данной функции в декартовых координатах для 
:
|
| ||||
φ
Из этого графика видно, что при 
имеем 
.
Поэтому требуемый график будет находиться в секторах, соответствующих данным значениям j, а также в секторах, симметричных им относительно начала координат (в силу того, что перед 
стоит чётный коэффициент).
Учитывая характер изменения r в этих промежутках (от 0 до 1 и затем снова до 0) получим следующий график (восьмилепестковую розу):
ПРИМЕР 12. Исследовать сходимость ряда 
Проверим, выполняется ли необходимое условие сходимости знакоположительного ряда. Найдём предел общего члена ряда
.
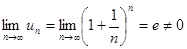Так как данный предел не равен нулю, то не выполняется необходимое условие сходимости ряда, следовательно, он расходится.
ПРИМЕР 13. Разложить функцию 
в ряд по степеням х.
Решение.
Разложим функцию в ряд Маклорена. Учитывая, что 
, разложим функцию на сумму двух более простых:
.
Далее преобразуем:
.
Воспользуемся разложением:
.
|
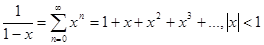(при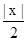 
<1, т.е. при 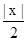<2)
то есть 
.
Аналогично получим второе разложение:
.
Тогда:
.
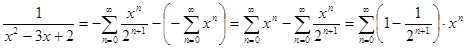Окончательно получаем:
ПРИМЕР 14. Найти неопределённый интеграл 
.
Решение.
Введем подстановку 
, откуда 
. Тогда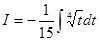 
. Находим полученный табличный интеграл и возвращаемся к прежней переменной:
.
ПРИМЕР 15. Найти неопределённый интеграл 
.
Решение.
Подведем под знак дифференциала знаменатель подынтегральной дроби:
.
ПРИМЕР 16. Найти неопределённый интеграл 
.
Решение.
Применим формулу интегрирования по частям: 
. В данном случае:
. Подставляя эти выражения в формулу, получим:
.
ПРИМЕР 17. Вычислить интеграл 
или установить его расходимость.
Решение.
Точка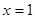 
является особой точкой, поскольку подынтегральная функция имеет в ней бесконечный разрыв. Поэтому:
- получили бесконечный предел.
Таким образом, данный интеграл расходится.
ПРИМЕР 18. Решить уравнение: 
.
Решение.
Данное уравнение является дифференциальным уравнением первой степени с Разделяющимися переменными. Разделим переменные:
.
Проинтегрируем части последнего равенства:
.
Отсюда:
.
Окончательно имеем:
- общее решение данного уравнения.
ПРИМЕР 19. Решить уравнение: 
.
Решение.
Данное дифференциальное уравнение относится к типу однородных дифференциальных уравнений
,
которые решаются с помощью подстановки
.
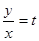Отсюда:
.
После подстановки в исходное уравнение получим:
.
Это – уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя обе части, получим:
Используя обратную подстановку, получим:
Окончательно имеем обще решение в виде:
.
Теперь, чтобы найти частное решение, подставляем в общее решение начальное условие:
.
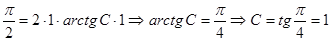Искомое частное решение:
.