Машина Поста – абстрактная вычислительная машина, предложенная Эмилем Леоном Постом, которая отличается от машины Тьюринга большей простотой.

14)

15) Примитивно рекурсивными называют функции, которые можно получить с помощью операций подстановки и рекурсии из следующих базисных функций: константы 0,операции прибавления единицы s: x 7! x + 1 и семейства функций проекции: это семейство для каждого k содержит k штук k-местных функций _i k(x1;:::; xk) = xi.

16) Сложение. Функция «x; y» sum(x; y) = x +y получается с помощью рекурсии:

sum(x; 0) = x;

sum(x; y + 1) = sum(x; y) + 1:

Надо, конечно, представить правую часть второго равенства как результат подстановки. Формально говоря,

h(x; y; z) в определении рекурсии надо положить равным s(z), где s | функция прибавления единицы.

Умножение. Функция hx; yi 7! prod(x; y) = xy получается с помощью рекурсии (с использованием сложения):

prod(x; 0) = 0;

prod(x; y + 1) = prod(x; y) + x:

17) Усечённое вычитание. Мы говорим об «усечённом вы-

читании» x _−

y = x − y при x > y и x _−

y = 0 при x < y,

поскольку мы имеем дело только с натуральными (целыми неотрицательными) числами. Одноместная функция усечённого вычитания единицы определяется рекурсивно:

0 1 = 0;

(y + 1) 1 = y:

(Рекурсия здесь формальна, так как предыдущее значение не используется.) После этого усечённое вычитание

для произвольных аргументов можно определить так:

x 0 = x;

x (y + 1) = (x y) 1:

18) Будем называть множество примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна

Свойства x = y и x 6= y примитивно рекурсивны (x = y тогда и только тогда, когда (x _−y) + (y _−x) = 0).

Функция f(x), заданная соотношением

f(x) = [ if R(x) then g(x) else h(x) ˛ ];

Теперь можно записать формулу для прибавления единицы по модулю n (для чисел, меньших n):

x + 1 mod n = [ if x + 1 = n then 0 else x + 1 ˛ ]После этого функцию x mod n (остаток от деления на n)можно определить рекурсивно:

0 mod n = 0;

(x + 1) mod n = (x mod n) + 1 mod n:

 

19)

20)

21) Покажем теперь, что если график некоторой функции f примитивно рекурсивен и её значения ограничены сверху некоторой примитивно рекурсивной функцией g, то сама функция f примитивно рекурсивна. В самом деле, если r | характеристическая функция графика, то есть r(x; y) = 1 при y = f(x) и r(x; y) = 0 при y 6= f(x)

(для простоты мы рассматриваем случай функций одного аргумента), то

f(x) =1X

y=0

y · r(x; y);

а суммирование можно ограничить сверху выражением g(x) и воспользоваться примитивной рекурсивностью ограниченной суммы.

Отсюда легко вывести следующее утверждение: если функция g и свойство R(x; y) примитивно рекурсивны,

то функция x 7! f(x) = наименьшее y 6 g(x), для которого R(x; y) (если для некоторого x такого y нет, то полагаем значение функции равным, скажем, g(x)+1) будет примитив-

но рекурсивной. В самом деле, график функции f легко описать с помощью ограниченных кванторов.

Такой способ определения функции называют ограниченным оператором минимизации | в отличие от не-

ограниченного, где нет заранее известной границы g(x).

Как мы увидим, в неограниченном случае получающаяся функция не обязана быть примитивно рекурсивной. Ограниченный оператор минимизации можно использовать, чтобы убедиться, что функция x 7! (минималь-

ное простое число, большее x)

 

22) Совместная рекурсия. Пусть две одноместные функ-

ции f и g заданы соотношениями:

f(0) = a;

g(0) = b;

f(n + 1) = F(n; f(n); g(n));

g(n + 1) = G(n; f(n); g(n));

где a и b | некоторые числа, а функции F и G | примитивно рекурсивные функции трёх аргументов. Покажем,что тогда функции f и g примитивно рекурсивны.

Чтобы доказать это, нам потребуется примитивно рекурсивная нумерация пар|такая функция hx; yi! [x; y]

(номер пары мы обозначаем квадратными скобками), которая была бы примитивно рекурсивна вместе с двумя обратными функциями (дающими по номеру пары её первый и второй члены). Тогда мы сможем написать рекурсивное определение для функции h(n) = [f(n); g(n)]:

h(0) =[a; b];

h(n + 1) =[F(n; p1(h(n)); p2(h(n)));

G(n; p1(h(n)); p2(h(n)))];

 

23) Возвратная рекурсия. Следующее утверждение показывает, что при рекурсивном определении можно использовать не только значение в предыдущей точке, но и любое предшествующее значение.Теорема 74. Пусть функция g одного аргумента примитивно рекурсивна, причём g(x) < x при x > 0; пустьF |примитивно рекурсивная функция двух аргументов; пусть c | произвольная константа. Тогда функция h, определённая соотношениямиh(0) = c; h(x) = F(x; h(g(x))) при x > 0

примитивно рекурсивна.

_ Чтобы доказать эту теорему, используем следующую нумерацию конечных последовательностей натуральных чисел: номером пустой последовательности считаем число 1, номером одноэлементной последовательности hai считаем число 2a+1, последовательность ha; bi имеет номер 2a+13b+1, последовательность ha; b; ci имеет номер 2a+13b+15c+1 и так далее (основания степеней | простые числа). Будем обозначать номер последователь-

ности ha; b;:::; zi через [a; b;:::; z]. Эта нумерация в некотором смысле примитивно рекурсивна. Конечно, буквально это понимать нельзя, так как нумерация представляет собой «функцию с переменным числом аргументов». Но разные связанные с ней функции примитивно рекурсивны. В частности, таковы функции

• Length(x) = длина последовательности с номером x;

• Select(i; x) = i-ый член последовательности с номером x;

• Append(x; y) = номер последовательности, которая получается приписыванием числа y к последовательности с номером x.

 

24) Функции, получающиеся из базисных (нуля, проекции

и прибавления единицы) с помощью операторов подстановки, примитивной рекурсии и минимизации, называются частично рекурсивными. Если такая функция оказывается всюду определённой, то её называют общерекурсивной функцией.

 

25). чтобы задать машину Тьюринга, надо указать следующие объекты:

• произвольное конечное множество A (алфавит);

его элементы называются символами;

• некоторый выделенный символ a0 2 A (пробел, или

пустой символ);

• конечное множество S, называемое множеством состояний;

• некоторое выделенное состояние s0 2 S, называемое начальным;

• таблицу переходов, которая определяет поведение машины в зависимости от состояния и текущего

символа (см. ниже);

• некоторое подмножество F _ S, элементы которого называются заключительными состояниями

(попав в такое состояние, машина останавливает-

ся).

Остаётся договориться, как мы подаём информацию на вход машины и что считается резуль татом её работы. Будем считать, что алфавит машины, помимо пробела, содержит символы 0 и 1 (а также, возможно, ещё какие-то символы). Входом и выходом машины будут конечные последовательности нулей и единиц (двоичные слова). Входное слово записывается на пустойленте, головка машины ставится в его первую клетку, машина приводится в начальное состояние и запускается. Если машина останавливается, результатом считает ся двоичное слово, которое можно прочесть, начиная с позиции головки и двигаясь направо (пока не появится символ, отличный от 0 и 1).

26) Схема:

27) Алгоритм перехода от п к п + 1 в деся­тичной системе счисления. Решается задача следующего типа: Дана десятичная запись числа п (т. е. представление натурального числа п в десятичной системе счисления);

требуется указать десятичную запись числа п + 1.

Для этого берется внешний алфавит, состоящий из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и пустого знака Д. Машина может пребывать лишь в двух состоя­ниях: q0 (рабочее состояние) и! (оста­новка). Заданное число п, а также ре­зультирующее число п + 1 будут запи­саны в десятичной системе, причем цифры будут помещаться по одной в ячейке (ячейки следуют подряд одна за другой без пропусков). Соответствующая функ­циональная схема дана на рис. 15 в виде той части указанной на нем таблицы, которая получится, если не учитывать в ней последнюю строку и последний столбец (смысл расширенной таблицы будет пояснен несколько позже). Пусть к началу работы в поле зрения установлена цифра разряда единиц числа п, а машина настроена в состояние qo\ если эта цифра отлична от 9, то машина остановится уже после первого такта работы, в котором происходит замена этой цифры другой цифрой в соот­ветствии со схемой. Если же последняя цифра 9, то ма«шина заменяет ее нулем и производит сдвиг влево (к соседнему, более высокому разряду) и продолжает пребывать в рабочем состоянии q0 (таким образом обес­печивается перенос единицы в более высокие разряды). Если число оканчивается k девятками, то машина за­кончит работу в точности после k + 1 такта.

28) Алгоритм перевода в десятичную си­стему счисления. Построим функциональную схему машины (алгоритма), решающей задачу следую­щего типа:

Дана конечная совокупность палочек, вписанных в ячейки, взятые подряд без пропусков (такие совокуп­ности будем называть наборами палочек)', требуется записать в десятичной системе число этих палочек.

Короче: пересчитать набор палочек.

Такая схема задана на рис. 18. Для того, чтобы убе­диться в том, что эта схема действительно описывает нужную машину (алгоритм), полезно сравнить ее со схемой расширенной таблицы рис. 15. Столбец q0 в схеме рис.. 18 отличается от столбца qo в схеме рис. 15 лишь тем, что вместо состояния «!» в нем всюду фигурирует новое состояние q?, различие столбцов q\ не имеет суще­ственного значения в работе схемы рис. 15. Поэтому, если на ленте задана десятичная запись числа п, а пра­вее ее — набор палочек, если, далее, в поле зрения ма­шины, как и прежде, установлена самая правая палочка,а сама машина настроена в состоянии qu то в машине будет вначале протекать такой же процесс, как и при схеме рис. 15; именно палочка набора будет стерта, а запись числа п будет заменена записью числа ti + 1. Однако в то время как согласно схеме рис. 15 на этой стадии процесса появится состояние!, т. е. процесс пре­кращается, согласно схеме рис. 18 появляется состояние q2 и процесс продолжается

29) Рассмотрим теперь, как выглядит в машине Тьюринга алгоритм Евклида для нахождения общего наибольшего делителя чисел а, Ь. Этот алгоритм был уже ранее описан нами дважды: первый раз в виде словесного предписания, а второй раз в виде программы для электронной машины с автома­тическим управлением. На этот раз алгоритм мы зада­дим в виде функциональной схемы Тьюринговой ма­шины и проследим процесс вычисления в машине. Этот процесс складывается из чередующихся попеременно циклов сравнения и циклов вычитания, соответствующих элементарным операциям сравнения и вычитания в электронной машине Соответствующая функциональ­ная схема изображена на рис. 8; ее внешний алфавит состоит из четырех знаков:

Л, |, а, Р-

Натуральные числа будут по-прежнему изображаться соответствующими наборами палочек. Во избежание та­ких деталей, которые не связаны с существом дела и способны лишь усложнить наши рассмотрения, усло­вимся наборы палочек, изображающие заданные два числа, располагать на ленте один за другим без про­пусков и не отделяя их звездочкой, причем в начале процесса в поле зрения машины установлена самая пра­вая палочка в наборе первого числа. После подробного разбора, который будет приведен ниже, читатель в ка­честве упражнения, без особого труда, сумеет изменить предложенную функциональную схему так, чтобы она обеспечивала правильную работу машины и при другом способе задания условий задачи (например, если на­боры отделены звездочкой, а в поле зрения машины установлена какая-нибудь пустая ячейка).

 

30)

31) До сих пор придерживались той точки зрения, что различные алгоритмы осуществляются в различных ма­шинах Тьюринга, отличающихся своими- функциональ­ными схемами. Однако можно построить универсальную тьюрингову машину, способную в известном смысле вы­полнять любой алгоритм, а значит способную выполнять работу любой тьюринговой машины.

Для того чтобы лучше уяснить себе, как это делается, представим себе следующий эксперимент. Пусть на ленту машины подана начальная информация 91, и пред­положим, что некоторому человеку предложено указать, как будет перерабатывать машина эту информацию и во что она переработает ее окончательно. Если этот человек знаком с принципами работы тьюринговых ма- ший, то достаточно ему сообщить, кроме этой начальной информации St, еще функциональную схему машины. Тогда человек, подражая работе машины и выпи­сывая нужные конфигурации так, как мы это сделали при разборе алгоритма Евклида, сможет получить тот же результат, что и машина. Но это как раз и означает, что такой человек способен выполнять работу любой тьюринговой машины, если ему только задана ее функ­циональная схема. Сам же процесс подражания машине в соответствии с ее функциональной схемой может быть регламентирован в виде точного предписания, которое можно сообщить человеку, не имеющему ни малейшею понятия о машинах Тьюринга. Если человека, распола­гающего таким предписанием, которое естественно на­зывать алгоритмом подражания, снабдить функциональ­ной схемой какой-либо машины Тьюринга и, кроме того, некоторой начальной конфигурацией, изображенной на ленте, то ок окажется способным в точности подражать работе соответствующей машины и в результате выдаст тот же результат. Подобный алгоритм подражания можно было бы задать хотя бы в виде следующей си­стемы указаний:

Указание 1. Обозревай на ленте ячейку (един­ственную), под которой подписана буква.

Указание 2. Отыщи в таблице [1]) столбец, обо­значенный такой же буквой, какая подписана под обо­зреваемой ячейкой.

Указание 3. В найденном столбце обозревай ту тройку букв, которая расположена на пересечении со строкой, обозначенной такой же буквой, какая вписана в обозреваемой ячейке.

Указание 4. Замени букву из обозреваемой ячейки первой буквой из обозреваемой тройки.

Указание 5. Если в обозреваемой тройке второй буквой является!, то остановись: процесс окончен.

Указание 6. Если в обозреваемой тройке второй буквой является Я, то замени букву, подписанную под обозреваемой ячейкой, третьей буквой из обозревае­мой тройки.

Указание 7. Если в обозреваемой тройке второй буквой является J1, то сотри букву, подписанную под обозреваемой ячейкой, и л е в е е ее запиши третью букву из обозреваемой тройки.

Указание 8. Если в обозреваемой тройке второй буквой является П, то сотри букву, подписанную под обозреваемой ячейкой, и п р а в е е ее запиши третью букву из обозреваемой тройки.

32) Непосредственная подача функциональной схемы подражаемой машины и соответствующей конфигурации на ленту универсальной машины в качестве исходной информации невозможна. Действительно, в универсаль­ной машине, как и во всякой тьюринговой машине, ин­формация изображена буквами, расположенными на ленте одномерно, т. е. в одной строке, образуя одно или несколько слов во внешнем алфавите машины. В то же время функциональные схемы мы до сих пор зада­вали посредством «двумерных» таблиц, в которых буквы располагаются несколькими строками; аналогично об­стоит дело с конфигурациями, в которых буквы состоя­ний записаны под буквами внешнего алфавита (под лентой).

Универсальная машина (как и всякая тьюрингова машина) может располагать лишь фиксированным ко­нечным внешним алфавитом. Между тем, она должна быть приспособлена к приему в качестве исходной информации всевозможных схем и конфигураций, в ко­торых могут встречаться буквы из разнообразных алфа­витов со сколь угодно большим числом различных букв.

 

33) Всякая функция, вычислимая с помощью машины Тьюринга, является частично рекурсивной.

Пусть f— вычислимая с помощью машины Тью­ринга (обозначим эту машину через М) функция одного аргумента. Рассмотрим свойство T(x,y,t), состоящее в том, что машина М на входе х даёт ответ у за время не более чем t. Как мы видели выше, по входу машины Тью­ринга и по времени t можно примитивно рекурсивно вы­числить её состояние в момент ясно, что можно также узнать, закончила ли она работу, и если да, то был ли от­вет равен у. Итак, свойство Т примитивно рекурсивно.

Т.Всякая частично рекурсивная функция вычислима на машине Тьюринга.

Всякая частично рекурсивная функция / представима в виде

F(x) = a(nz(b(x,z) = 0)),

где а и b — некоторые примитивно рекурсивные функ­ции.

 

34) Те́зис Чёрча—Тью́ринга — фундаментальное утверждение для многих областей науки, таких, как теория вычислимости, информатика, теоретическая кибернетика и др. Это утверждение было высказано Алонзо Чёрчем и Аланом Тьюрингом в середине 1930-х годов.

В самой общей форме оно гласит, что любая интуитивно вычислимая функция является частично вычислимой, или, эквивалентно, может быть вычислена с помощью некоторой машины Тьюринга.

Тезис Чёрча—Тьюринга невозможно строго доказать или опровергнуть, поскольку он устанавливает «равенство» между строго формализованным понятием частично вычислимой функции и неформальным понятием «интуитивно вычислимой функции».

Физический тезис Чёрча—Тьюринга гласит: Любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга.

 

35)

36) Машина с неограниченными регистрами является исполнителем, представляющим собой простой "идеализированный компьютер". Идеализация состоит в том, что каждый отдельный реальный компьютер ограничен как величиной чисел, которые поступают на вход, так и размером памяти (необходимой для запоминания промежуточных результатов), МНР лишена этих ограничений. Машина с неограниченными регистрами имеет неограниченно большую память, ячейки которой будем называть регистрами и обозначать Каждый регистр в любой момент времени содержит неотрицательное целое число.

				...
				...

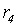
При этом только конечное множество регистров содержит числа, отличные от нуля. Все остальные регистры заполнены нулями. Это допущение предполагает, что каждый алгоритм использует только конечный объем памяти.

В список предписаний МНР входит четыре команды: команда обнуления Z(n); команда прибавления единицы S(n); команда переадресации T(m, n) и команда условного переходам J(m, n, q). Команды обнуления, прибавления единицы и переадресации называются арифметическими.

Обозначение команды	Действие, производимое МНР по данной команде
Z(n)
S(n)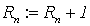
T(m, n)
J(m, n, q)	Если , то перейти к вычислению команды алгоритма с номером q.

37) 37. Всякий НАМ(нормальный алгоритм Маркова) определяется конечным упорядоченным множеством пар слов алфавита, называемых подстановками. В паре слов подстановки левое (первое) слово непустое, а правое (второе) слово может быть пустым символом. Для наглядности левое и правое слово разделяются стрелкой. Например,

1.

2.

3.

4.

В качестве данных алгоритма берется любая непустая строка символов. Работа НАМ состоит из последовательности совершенно однотипных шагов. Шаг работы алгоритма может быть описан следующим образом:

1. В упорядоченной последовательности подстановок ищем самую первую подстановку, левое слово которой входит в строку данных.

2. В строке данных ищем самое первое (левое) вхождение левого слова найденной подстановки.

3. Это вхождение в строке данных заменяем на правое слово найденной подстановки (преобразование данных).

Шаг работы алгоритма повторяется до тех пор, пока

• либо не возникнет ситуация, когда шаг не сможет быть выполнен из-за того, что ни одна подстановка не подходит (левое слово любой подстановки уже не входит в строку данных) - правило остановки;
• либо не будет установлено, что процесс подстановок не может остановиться.

Пример: , .

НАМ увеличения десятичного числа на 1:

Приведем работу построенного алгоритма для чисел 79 и 99:

.

Тезис: всякий алгоритм может быть нормализован т. е. задан нормальным алгоритмом Маркова

 

Машина Поста – абстрактная вычислительная машина, предложенная Эмилем Леоном Постом, которая отличается от машины Тьюринга большей простотой.

Принцип работы:

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты. Каждая секция ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит. Работа машины Поста определяется программой, состоящей из конечного числа строк. Всего команд шесть: → j сдвиг вправо перейти к j строке. ← j сдвиг влево, N. 1 J запись метки N. a(альфа)j удаление метки перейти к j строке.?j1,j2 если в ячейке нет метки, то перейти к j1,если в ячейке есть место, то к j2 строке.!-остановка

Ограничим ленту с одной стороны и покажем, что машина Тьюринга справой или левой полулентой эквивалентна машине Тьюринга с бесконечной лентой. Говорят, что функция, правильно вычислимая на машине Тьюринга с обычной лентой,правильно вычислима и на машине Тьюринга с правой полулентой, т.е. для любой машины. Тьюринга Т существует эквивалентная ей машина с правой полулентой TR. Идея доказательства этого утверждения основана на следующих предпосылках: а) рабочая область ленты ограничена двумя маркерами: неподвижным - слева и подвижным - справа; б) на внутренней части ограниченной области машина Тьюринга с полулентой должна работать как обычная машина Тьюринга, а при выходе на маркеры она должна освобождать рабочее пространство, для этого правый маркер может сдвигаться вправо, а при выходе налевый маркер необходимо сдвинуть всю цепочку вправо; в) полученный результат, находящийся между маркерами, в конце работы машиныТьюринга нужно сдвинуть вплотную к левому маркеру.Машина Тьюринга может вычислять функцию с восстановлением, то есть с сохранением исходных данных. Это позволяет получить на ленте сначала результат, а затем – исходные данные или наоборот.

39) Недетерминированная машина Тьюринга

Обобщение детерминированной машины Тьюринга, в которой, при каждом переходе, можно выполнять переход одновременно в несколько (константа) состояний — можно считать, что происходит «клонирование» машины (состояние, содержимое лент, положение головок).

Таким образом, для каждого массива входных данных имеется не один, а несколько (в общем случае — экспоненциальное число) путей, по которым может развиваться вычисление.

Недетерминированная машина Тьюринга выдаст ответ 1, если существует хотя бы один путь развития вычисления, на котором выдается ответ 1, и 0 — в противном случае (таким образом, ответы «ДА» и «НЕТ» в случае недетерминированных вычислений несимметричны).

40)

41) Понятие сложности алгоритма(временной сложности). Порядок роста функций. Длина описания задачи.

Временная сложность — основной параметр, характеризующий алгоритм; определяется как число шагов, выполняемых алгоритмом в худшем случае, обычно рассматривается как функция размера задачи, представленной входными данными. Обычно под размером теоретико-графовой задачи понимается число вершин графа , число дуг или пара . Под шагом алгоритма понимается выполнение одной из команд некоторой гипотетической машины. Поскольку при таком определении шага сложность алгоритма зависит от конкретного вида машинных команд, во внимание принимается асимптотическая сложность, т.е. асимптотическая скорость увеличения числа шагов алгоритма, когда размерность задачи неограниченно растет. Ясно, что при двух произвольных "разумных" способах перевода алгоритма в последовательность машинных команд соответствующие сложности различаются не более чем на мультипликативную константу, а их скорость роста одинакова.

Те, кто часто решает алгоритмические задачи, знают, что решить их можно по-разному и, что процессы могут значительно различаться по количеству вычислительных ресурсов, которые они потребляют. Удобным способом описания этих различий является понятие порядка(скорости) роста, которое дает общую оценку ресурсов, необходимых процессу при увеличении его входных данных.

Пусть n — параметр, измеряющий размер задачи, и пусть R(n) — количество ресурсов, необходимых процессу для решения задачи размера n. R(n) может измерять количество используемых целочисленных регистров памяти, количество исполняемых элементарных
машинных операций, и так далее. В компьютерах, которые выполняют определенное число операций за данный отрезок времени, требуемое время будет пропорционально необходимому числу элементарных машинных операций.

42)