ЧУВАШСКИЙ ФИЛИАЛ
ФАКУЛЬТЕТ ЭКОНОМИКИ И УПРАВЛЕНИЯ
СПЕЦИАЛЬНОСТЬ «»
КОНТРОЛЬНАЯ РАБОТА
по ЭКОНОМЕТРИКЕ
Вариант №....
Выполнил студент курса
Группы
(Ф.И.О. студента)
Проверил
(Ф.И.О., должность)
Оценка ____________________________
(подпись) (расшифровка подписи)
Чебоксары 200...
ЗАДАНИЕ 1
| Xi | ||||||
| Yi |
Для расчета параметров a и b линейной регрессии 
решим систему нормальных уравнений относительно a и b:
По исходным данным рассчитаем 
, 
, 
, 
, 
, 
, 
, 
, 
, 
и внесем в таблицу 1.
Таблица 1
| x | y | xy | x2 | y2 | |
| Итого | |||||
| Среднее значение | 15,0000 | 86,5000 | 1326,6667 | 236,6667 | 7559,8333 |
| 3,4157 | 8,8081 | |||
| 11,6667 | 77,5833 |
Вычислим среднее квадратическое отклонения x и y:
,
.
Вычислим оценки коэффициентов регрессии:
,
.
Уравнение регрессии: 
. С увеличением цены на 1 ед. дневной спрос на некоторый вид товара увеличивается в среднем на 2,5 ед.
Рассчитаем линейный коэффициент парной корреляции:
.
Связь достаточно сильная, прямая.
Построим прямую регрессии y на x (рис.1).
рис.1
ЗАДАНИЕ 2
| Xi | ||||||||||
| Yi |
Для расчетов параметров уравнения линейной регрессии строим расчетную таблицу 2.
Таблица 2
| x | y | xy | x2 | y2 | yx | y-yx | (y-yx)2 | |
| 4,8333 | -1,8333 | 3,3611 | ||||||
| 4,8333 | 0,1667 | 0,0278 | ||||||
| 4,8333 | 0,1667 | 0,0278 | ||||||
| 6,5000 | -1,5000 | 2,2500 | ||||||
| 6,5000 | 1,5000 | 2,2500 | ||||||
| 6,5000 | 2,5000 | 6,2500 | ||||||
| 8,1667 | -3,1667 | 10,0278 | ||||||
| 8,1667 | 0,8333 | 0,6944 | ||||||
| 8,1667 | 0,8333 | 0,6944 | ||||||
| 6,5000 | 0,5000 | 0,2500 | ||||||
| Итого | 65,0000 | 0,0000 | 25,8333 | |||||
| Среднее значение | 2,0000 | 6,5000 | 14,0000 | 4,6000 | 46,5000 | |||
|
| 0,7746 | 2,0616 | ||||||
|
| 0,6000 | 4,2500 |
Вычислим оценки коэффициентов регрессии:
,
.
Получено уравнение регрессии: 
. С увеличением количества продавцов на 1 чел. количество проданных автомобилей возрастает в среднем на 1,6667 машин.
Тесноту линейной связи оценит коэффициент корреляции:
.
Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стъюдента.
Выдвигаем гипотезу 
о статистически незначимом отличии показателей от нуля.
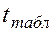для числа степеней свободы 
и 
составит 2,3060 (приложение 2).
Определим случайные ошибки 
, 
, 
:
,
,
,
.
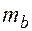Тогда
,
,
.
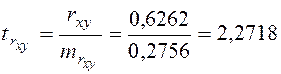Так как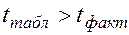 
, то гипотеза не отклоняется и признается случайная природа формирования 
, 
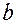или 
.
Проведем анализ дисперсии зависимой переменной.
Остаточная сумма квадратов отклонений 
исходя из таблицы 2 равна 25,8333, а сумма квадратов отклонений, обусловленная регрессией, вычисляется по формуле:
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака Y характеризует коэффициент детерминации:
.
Это означает, что 39% вариации количества проданных автомобилей (Y) объясняется вариацией фактора X – количества продавцов.
Проверим на уровне значимости 5% гипотезу о линейной зависимости числа продаж от числа продавцов с помощью F-критерия Фишера.
Выдвигаем гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи.
для уровня значимости и 
, 
составит 5,32 (приложение 1).
.
Так как 
, то гипотеза не отклоняется. Этот результат можно объяснить невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
ЗАДАНИЕ 3
Уравнение линейной регрессии будем искать в виде 
(i=1,2,…,25). Вычислим средние значения переменных 
, 
, 
, 
, 
:
, 
,
, 
,
.
Вычислим оценки коэффициентов регрессии:
,
.
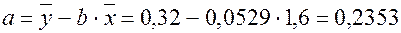Получено уравнение регрессии: 
.
Определим прогнозное значение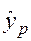 
при 
:
.
Построим 95%-ный доверительный интервал. Произведем необходимые вычисления:
,
,
,
,
.
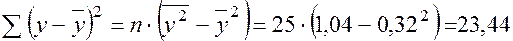Вычислим среднюю стандартную ошибку прогноза:
.
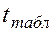для числа степеней свободы 
и составит 2,0687 (приложение 2).
Вычислим предельную ошибку прогноза:
.
Построим доверительный интервал прогноза:
,
,
.
ЗАДАНИЕ 4
| Значения Xi | |||||||||
| 0,25 | 0,50 | 0,75 | 1,00 | 1,25 | 1,50 | 1,75 | 2,00 | 2,25 | 2,50 |
| Значения Yi | |||||||||
| 0,3 | 1,2 | 2,8 | 5,2 | 8,1 | 11,0 | 16,8 | 16,9 | 24,7 | 29,4 |
4а. Построим уравнение линейной регрессии 
. Для расчетов используем данные таблицы 3.
Таблица 3
| x | y | xy | x2 | y2 | |
| 0,25 | 0,3 | 0,0750 | 0,0625 | 0,0900 | |
| 0,5 | 1,2 | 0,6000 | 0,2500 | 1,4400 | |
| 0,75 | 2,8 | 2,1000 | 0,5625 | 7,8400 | |
| 5,2 | 5,2000 | 1,0000 | 27,0400 | ||
| 1,25 | 8,1 | 10,1250 | 1,5625 | 65,6100 | |
| 1,5 | 16,5000 | 2,2500 | 121,0000 | ||
| 1,75 | 16,8 | 29,4000 | 3,0625 | 282,2400 | |
| 16,9 | 33,8000 | 4,0000 | 285,6100 | ||
| 2,25 | 24,7 | 55,5750 | 5,0625 | 610,0900 | |
| 2,5 | 29,4 | 73,5000 | 6,2500 | 864,3600 | |
| Итого | 13,7500 | 116,4000 | 226,8750 | 24,0625 | 2265,3200 |
| Среднее значение | 1,3750 | 11,6400 | 22,6875 | 2,4063 | 226,5320 |
|
| 0,7181 | 9,5416 | |||
|
| 0,5156 | 91,0424 |
Вычислим оценки коэффициентов регрессии:
,
.
Получено уравнение линейной регрессии: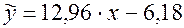 
.
Рассчитаем линейный коэффициент парной корреляции:
.
4б. Построению уравнения степенной регрессии 
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
;
, где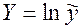 
, 
, 
.
Для расчетов используем данные таблицы 4.
Таблица 4
| № | Y | X | YX | Y2 | X2 | yx | y-yx | (y-yx)2 |
| -1,2040 | -1,3863 | 1,6691 | 1,4496 | 1,9218 | 0,3095 | -0,0095 | 0,0001 | |
| 0,1823 | -0,6931 | -0,1264 | 0,0332 | 0,4805 | 1,2324 | -0,0324 | 0,0011 | |
| 1,0296 | -0,2877 | -0,2962 | 1,0601 | 0,0828 | 2,7657 | 0,0343 | 0,0012 | |
| 1,6487 | 0,0000 | 0,0000 | 2,7181 | 0,0000 | 4,9077 | 0,2923 | 0,0855 | |
| 2,0919 | 0,2231 | 0,4668 | 4,3759 | 0,0498 | 7,6571 | 0,4429 | 0,1961 | |
| 2,3979 | 0,4055 | 0,9723 | 5,7499 | 0,1644 | 11,0132 | -0,0132 | 0,0002 | |
| 2,8214 | 0,5596 | 1,5789 | 7,9602 | 0,3132 | 14,9753 | 1,8247 | 3,3297 | |
| 2,8273 | 0,6931 | 1,9597 | 7,9937 | 0,4805 | 19,5426 | -2,6426 | 6,9833 | |
| 3,2068 | 0,8109 | 2,6005 | 10,2836 | 0,6576 | 24,7147 | -0,0147 | 0,0002 | |
| 3,3810 | 0,9163 | 3,0980 | 11,4311 | 0,8396 | 30,4911 | -1,0911 | 1,1905 | |
| итого | 18,3829 | 1,2415 | 11,9226 | 53,0554 | 4,9900 | 117,6094 | -1,2094 | 11,7878 |
| срзнач | 1,8383 | 0,1241 | 1,1923 | 5,3055 | 0,4990 | 1,1788 | ||
|
| 1,3879 | 0,6954 | ||||||
|
| 1,9262 | 0,4836 |
Рассчитаем 
и :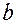
,
.
Получим уравнение линейной регрессии: 
.
Выполнив его потенцирование, получим:
.
Подставляя в данное уравнение фактические значения , получаем теоретические значения результата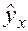 
. По ним рассчитаем показатели тесноты связи – индекс корреляции 
:
.
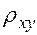Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимность.
4в. Построению уравнения показательной регрессии 
предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
;
, где , ,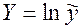 
.
Для расчетов используем данные таблицы 5.
Таблица 5
| № | Y | x | Yx | Y2 | x2 | yx | y-yx | (y-yx)2 |
| -1,2040 | 0,25 | -0,3010 | 1,4496 | 0,0625 | 0,8074 | -0,5074 | 0,2574 | |
| 0,1823 | 0,5 | 0,0912 | 0,0332 | 0,2500 | 1,2739 | -0,0739 | 0,0055 | |
| 1,0296 | 0,75 | 0,7722 | 1,0601 | 0,5625 | 2,0100 | 0,7900 | 0,6240 | |
| 1,6487 | 1,6487 | 2,7181 | 1,0000 | 3,1715 | 2,0285 | 4,1148 | ||
| 2,0919 | 1,25 | 2,6148 | 4,3759 | 1,5625 | 5,0041 | 3,0959 | 9,5845 | |
| 2,3979 | 1,5 | 3,5968 | 5,7499 | 2,2500 | 7,8957 | 3,1043 | 9,6369 | |
| 2,8214 | 1,75 | 4,9374 | 7,9602 | 3,0625 | 12,4581 | 4,3419 | 18,8525 | |
| 2,8273 | 5,6546 | 7,9937 | 4,0000 | 19,6567 | -2,7567 | 7,5996 | ||
| 3,2068 | 2,25 | 7,2153 | 10,2836 | 5,0625 | 31,0151 | -6,3151 | 39,8801 | |
| 3,3810 | 2,5 | 8,4525 | 11,4311 | 6,2500 | 48,9366 | -19,5366 | 381,6797 | |
| итого | 18,3829 | 13,7500 | 34,6825 | 53,0554 | 24,0625 | 132,2291 | -15,8291 | 472,2349 |
| срзнач | 1,8383 | 1,3750 | 3,4683 | 5,3055 | 2,4063 | 47,2235 | ||
|
| 1,3879 | 0,7181 | ||||||
|
| 1,9262 | 0,5156 |
Рассчитаем и 
:
,
.
Получим уравнение линейной регрессии: 
.
Выполнив его потенцирование, получим:
.
Тесноту связи оценим через индекс корреляции :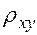
.
Связь умеренная.
4г. Гиперболическое уравнение 
линеаризуется при замене: 
. Тогда 
.
Для расчетов используем данные таблицы 6.
Таблица 6
| № | y | z | yz | y2 | z2 | yx | y-yx | (y-yx)2 |
| 0,3 | 4,0000 | 1,2000 | 0,0900 | 16,0000 | -6,0504 | 6,3504 | 40,3273 | |
| 1,2 | 2,0000 | 2,4000 | 1,4400 | 4,0000 | 6,4587 | -5,2587 | 27,6536 | |
| 2,8 | 1,3333 | 3,7333 | 7,8400 | 1,7778 | 10,6284 | -7,8284 | 61,2831 | |
| 5,2 | 1,0000 | 5,2000 | 27,0400 | 1,0000 | 12,7132 | -7,5132 | 56,4481 | |
| 8,1 | 0,8000 | 6,4800 | 65,6100 | 0,6400 | 13,9641 | -5,8641 | 34,3877 | |
| 0,6667 | 7,3333 | 121,0000 | 0,4444 | 14,7980 | -3,7980 | 14,4251 | ||
| 16,8 | 0,5714 | 9,6000 | 282,2400 | 0,3265 | 15,3937 | 1,4063 | 1,9777 | |
| 16,9 | 0,5000 | 8,4500 | 285,6100 | 0,2500 | 15,8405 | 1,0595 | 1,1226 | |
| 24,7 | 0,4444 | 10,9778 | 610,0900 | 0,1975 | 16,1879 | 8,5121 | 72,4553 | |
| 29,4 | 0,4000 | 11,7600 | 864,3600 | 0,1600 | 16,4659 | 12,9341 | 167,2906 | |
| итого | 116,4000 | 11,7159 | 67,1344 | 2265,3200 | 24,7963 | 116,4000 | 0,0000 | 477,3712 |
| срзнач | 11,6400 | 1,1716 | 6,7134 | 226,5320 | 2,4796 | 47,7371 | ||
|
| 9,5416 | 1,0521 | ||||||
|
| 91,0424 | 1,1070 |
Вычислим оценки коэффициентов регрессии:
,
.
Получено уравнение: 
.
Индекс корреляции:
.
По степенному уравнению регрессии получена наибольшая оценка тесноты связи: 
(по сравнению с линейной, показательной и гиперболической регрессиями).
ЗАДАНИЕ 5
1. Проверим идентификацию каждого уравнения и системы в целом.
Модель имеет три эндогенные (
, 
, 
) и три экзогенные (
, 
, 
) переменные.
Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.
Первое уравнение.
Н: эндогенных переменных – 2 (
, 
),
отсутствующих экзогенных – 1 (
).
Выполняется необходимое равенство: 1 + 1 = 2, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют 
и . Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
|
|
| |
| Второе | -1 |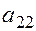 
|
| Третье | 
|
Вычислим определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в первом уравнении:
.
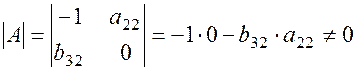Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Второе уравнение.
Н: эндогенных переменных – 3 (, , ),
отсутствующих экзогенных – 2 (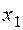
, 
).
Выполняется необходимое равенство: 2 + 1 = 3, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют 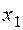и . Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
|
|
| |
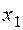
| Первое | 
| 
|
| Третье | 
| 
|
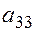
Вычислим определитель матрицы, составленной из коэффициентов при переменных, отсутствующих во втором уравнении:
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Третье уравнение.
Н: эндогенных переменных – 2 (, ),
отсутствующих экзогенных – 1 ().
Выполняется необходимое равенство: 1 + 1 = 2, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют и . Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
|
|
| |
| Второе | -1 | |
| Третье | 
|
|
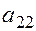
Вычислим определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в третьем уравнении:
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Таким образом, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
2. Найдем приведенную форму модели.
(1)
Подставим первое уравнения системы (1) во второе и получим:
,
. (2)
Уравнение (2) подставим в третье уравнение системы (1) и выразим :
,
(3)
В первое уравнение системы (1) подставим уравнение (3) и выразим :
Уравнение (3) подставим в (2) и выразим :
Таким образом, приведенная форма модели имеет вид:
где
, 
,
, 
,
, 
,
, 
,
.
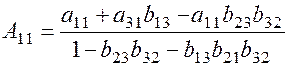ПРИЛОЖЕНИЯ
1. Таблица значений F-критерия Фишера при уровне значимости
| k1 k2 | 
| |||||||||
| 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 7,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,78 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| k1 k2 |
| |||||||||
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 | |
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | |
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | |
| 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | |
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 | |
| 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 | |
| 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 | |
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 | |
| 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | |
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 | |
|
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 | 1,00 |