ЛЕВИН В.М.
КОНСПЕКТ ЛЕКЦИЙ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ
«ОСНОВЫРАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ
С УЧЕТОМ НЕУПРУГИХ СВОЙСТВ МАТЕРИАЛА»
Макеевка ДонГАСА 2002
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ
СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ
Кафедра “Теоретическая и прикладная механика”
Левин В.М.
КОНСПЕКТ ЛЕКЦИЙ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ
«ОСНОВЫРАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ
С УЧЕТОМ НЕУПРУГИХ СВОЙСТВ МАТЕРИАЛА»
| Утверждено: на заседании кафедры теоретической и прикладной механики Протокол № 83 от 27.12.01 |
Макеевка ДонГАСА 2002
Конспект лекций. Строительная механика. Основы расчета стержневых систем с учетом неупругих свойств материала. /Сост.: Левин В.М.– Макеевка: ДонГАСА, 2002. – 25 с.
Рассматриваются особенности расчета стержневых систем при наличии пластических деформаций и деформаций ползучести, а также по стадии предельного равновесия.
Описываются особенности составления разрешающих уравнений и предлагаются методы их решения.
Составитель: проф. Левин В.М.
Ответственный
за выпуск проф. Мущанов В.Ф.
Лекция 1. Расчет стержневых систем из упругопластического материала
Методы строительной механики, изучавшиеся в нашем курсе, базируются на системе гипотез, одна из которых - предположение о линейной упругости материала (для одноосного деформирования - закон Гука, для неодноосного - обобщенный закон Гука). Однако закон Гука дает неполное описание деформативных свойств материала, свойства линейной упругости проявляются при ограниченных определенным пределом значениях напряжений, температур и при ограниченном времени деформирования. При большой длительности загружения и высоких температурах проявляются деформации ползучести, зависящие от режима загружения и деформирования (скорости и длительности отдельных стадий загружения и деформирования). При достаточно высоких уровнях напряжений к упругим деформациям, проявляющимся при умеренных воздействиях, добавляются пластические деформации. Деформативные свойства материала, отвечающие развитию деформаций ползучести (вязкости) и пластичности, достаточно сложны, и для их описания используются различные теории, отражающие с той или иной точностью поведение материалов в разнообразных условиях. При изучении материала настоящей темы мы ограничимся двумя частными случаями одноосного пластического деформирования (иногда говорят: «кратковременного деформирования»), совершенно не затрагивая вопросы учета деформаций ползучести (вязкости), то есть, в рассматриваемых нами случаях мы не затрагиваем задачи учета деформаций, зависящих от времени (или, более общо, от режима загружения и деформирования). Загружение считаем простым пропорциональным. Даже при таком существенном ограничении мы имеем дело с большим разнообразием закономерностей поведения материала, описываемых диаграммами деформирования. Так, строительные стали с умеренным содержанием углерода и без легирующих добавок (например, Ст3) имеют диаграммы типа показанных на рис.1,а.
На этой диаграмме четко различаются участки 1 - упругого деформирования, 2 - пластических деформаций и 3 - упрочнения. Высокоуглеродистые легированные стали (рис.1,б) не имеет площадку текучести, а участок 1 у них криволинейный. Бетон имеет различную прочность при сжатии и растяжении, и его диаграммы деформирования в обоих случаях криволинейны с самого низкого уровня (доля пластических деформаций достаточно велика и растет с увеличением нагрузки), причем имеют (при заданной скорости деформирования) не только восходящую, но и нисходящую ветви (рис.1,в). Для железобетона образование трещины, обычно допускаемое нормами, усложняет диаграмму деформирования элемента, что является предметом специального рассмотрения в курсе железобетонных конструкций. Дерево (рис.1,г) при растяжении волокон деформируется упруго и разрушается хрупко, а при сжатии его диаграмма деформирования криволинейна. Наиболее простая аппроксимация диаграмм деформирования, вполне пригодная для низкоуглеродистых сталей и, в меньшей степени, для сжатой древесины - диаграмма Прандтля (рис.1, д). Она характеризуется двумя параметрами - модулем упругости Е и пределом текучести sт,- однако, при этом остается за рамками анализа существенное свойство материала - он разрушается при достижении деформациями некоторой предельной величины, зависящей от материала и некоторых условий его работы (предельная растяжимость, предельная сжимаемость).
 |
Рис. 1. Некоторые часто встречающиеся диаграммы деформирования (для в и г сжатию соответствует e > 0, s > 0; отдельные диаграммы симметричны относительно начала координат
В некоторых случаях приходится учитывать его наличие, в некоторых принимается, что материал бесконечно деформируем. Для стали диаграмма деформирования принимается симметричной относительно начала координат, для бетона - несимметричной.
Более простая аппроксимация - предельный случай диаграммы Прандтля с Е = ¥ (eт=0); такая модель материала называется жестко-пластическим телом.
Два частных случая учета пластического деформирования при расчете конструкций, рассматриваемых в данной теме - это расчет с учетом физической нелинейности и расчет по стадии предельного равновесия. В первой лекции рассмотрим расчет с учетом физической нелинейности. При этом фактически решаются две задачи - дискретизация систем, как и в «упругой» задаче (МКР, МКЭ, ДКМ), и линеаризация нелинейной задачи, то есть, сведение ее к последовательности линейных задач, о чем и будет идти речь ниже. При этом нелинейность задачи обусловлена нелинейностью физических зависимостей; как любая нелинейность, она требует отказа от линейной зависимости между интенсивностью воздействия на систему и ее откликом на него (деформациями, перемещениями), то есть, от линейности системы и от принципа суперпозиции.
Рассмотрим некоторые элементарные аспекты расчета физических нелинейных систем на примере стержневой системы, выполненной из материала с симметричной диаграммой деформирования. Расчет может выполняться с использованием простых методов строительной механики упругих стержневых систем и методов решения нелинейных задач, рассматриваемых в прикладной математике. При этом в любом случае решение нелинейной задачи получается в результате решения той или иной последовательности линейно-упругих задач. Ограничимся для определенности методом конечных элементов в форме метода перемещений и случаем, близким к чистому изгибу (когда влиянием касательных напряжений на диаграмму деформирования и деформаций сдвига на перемещения можно пренебречь).
Проанализируем, как влияет наличие пластических деформаций на изгибную жесткость прямоугольного сечения (рис.2).
 |
Рис. 2. Эпюры в сечении балки (сечение симметричное)
Сплошными линиями показаны эпюры нормальных напряжений в сечении, соответствующие различным уровням загружения, причем большие номера соответствуют более высоким уровням. Так как при e > eт s = sт, при определенном уровне кривизны оси элемента (обозначим ее 
1, где 1 = 2eт /(h)) эпюра напряжений из треугольной превращается в трапециевидную; при этом М=М1=sтW=EI 1. На упругой стадии работы момент внутренних сил в сечении Ме=ЕI . На упругопластической стадии (при > 1) М=Ме-DМ, где по-прежнему Ме=EJk, DМ - момент, создаваемый напряжениями, “потерянными” на участках пластического деформирования abi и сid (соответствующие участки эпюры напряжений заштрихованы).
Элементарный анализ показывает, что
(1.1)
где 
Таким образом, имеются две возможности для определения момента внутренних сил в сечении:
1) прямое использование поправки DМ к моменту Ме, вычисленному в предположении упругой работы материала;
2) умножение момента Ме на поправочный коэффициент 
.
Интересно отметить, что 
то есть, М®0, что противоречит физическому смыслу задачи. Более глубокий анализ показывает, что аккуратное выполнение преобразований при переходе к пределу в случае использования второй возможности приводит к физически осмысленному результату:
(1.2)
Известно много методов расчета нелинейных систем (в прикладной математике им соответствуют те или иные методы решения нелинейных задач); рассмотрим три простейших метода, что позволит выявить основные особенности подхода к рассматриваемой проблеме.
1. Метод фиктивных нагрузок (метод начальных напряжений, метод Ильюшина). В прикладной математике ему соответствует модифицированный метод Ньютона. Этот метод вытекает из простых преобразований уравнения равновесия
q=d2M/dx2=EIyIV-d2DM/dx2
Это традиционный метод. В качестве нулевого приближения принимается решение “упругой” задачи. На каждой следующей итерации прикладывается фиктивная нагрузка интенсивностью
и решается “упругая” задача
(1.3)
где n - номер итерации,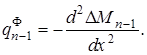 
В случае применения МКЭ
(1.4)
Преимущество метода фиктивных нагрузок - использование одной и той же матрицы жесткости на всех итерациях. Недостаток - снижение скорости сходимости при увеличении нагрузки; при определенном уровне нагрузки, близком к несущей способности системы, процесс может вообще перестать сходится.
2. Метод переменных параметров упругости. Это также итерационный метод. Моменты на концах незагруженного распределенной нагрузкой конечного стержневого изгибаемого элемента равны 
то есть, зависят от деформаций и, следовательно, неизвестных узловых обобщенных перемещений; аналогично и 
значит, МЖ элемента и системы зависят от узловых обобщенных перемещений [K] = [K(D)]. Итерационный процесс имеет вид
[Kn-1]{Dn} -{Р} = 0 (1.5)
где [Kn-1] = [K({Dn-1})], [K0] - МЖ упругого стержневого КЭ. Применение этого метода связано с пересчетом МЖ на каждом шаге итерации, но зато сходимость вблизи предельной точки ухудшается не столь заметно, как в случае метода фиктивных нагрузок.
3. Инкрементальный метод (метод приращений, шаговый метод). В прикладной математике ему соответствует метод продолжения (метод продолжения по параметру нагрузок). В этом методе последовательность “упругих” задач формируется благодаря последовательному наращиванию нагрузок (задаются приращения нагрузок) и определяются соответствующие приращения неизвестных обобщенных перемещений с использованием вычисляемых определенным образом “касательных” МЖ [K¢(D)] или их численных оценок, являющихся результатом приближенного прогноза значения [K¢(Dn)] по нескольким предыдущим значениям обычной МЖ [K(Dn-1)], K(Dn-2)] и т.д.:
[K¢(Dn){dDn+1}-{Pn+1}+{Pn}= 0 (1.6)
Применение этого метода связано с трудоемкими вычислениями касательной матрицы при наращивании нагрузок; в чистом виде метод применяется редко.
4. Шагово-итерационный метод обладает преимуществами методов 1 (или 2) и 3; он реализуется по схеме:
(1.7)
(1.8)
где m - номер шага увеличения нагрузки;
n - номер итерации на m-ом шаге нагрузки.
На каждом последующем шаге нагрузки итерации начинаются со значений фиктивных нагрузок или переменных МЖ, полученных после завершения итерационного цикла предыдущего шага. При этом скорость сходимости итерационного процесса может быть существенно увеличена.
В отличие от расчета линейно-упругих систем (в которых все зависимости, в том числе - зависимости между обобщенными усилиями и обобщенными деформациями) линейны, в рассматривавшихся здесь задачах эти зависимости (иногда называемые физическими соотношениями) преимущественно нелинейны; поэтому такие задачи называются физически нелинейными, а соответствующие расчеты - расчетами с учетом физической нелинейности.