1) Если первообразная функция не выражается через элементарные функции или вычисления определённого интеграла громоздка, то можно вычислять определённый интеграл приближённо с помощью степенных рядов. Для этого подынтегральную функцию раскладываем в степенной ряд. Если интервал интегрирования принадлежит области сходимости степенного ряда, то на этом интервале ряд можно почленно интегрировать. Подставляя пределы интегрирования, получим числовой ряд. Вычисляя сумму этого ряда с заданной точностью, получим приближённое значение интеграла с заданной точностью.
Пример 1. вычислить приближённое значение интеграла.
с точностью до 0,0001.
Используя формулу (2.25), разложим подынтегральную функцию в степенной ряд
Этот ряд сходится на интервале (-1;1), а поэтому равномерно сходиться на отрезке 
и, следовательно, его можно почленно интегрировать на этом отрезке
Поскольку получившийся числовой ряд является знакочередующимся, то абсолютная величина остаточного члена не превосходит абсолютную величины первого отброшенного члена. По условию точность вычисления 
Так как 
то достаточно взять сумму первых трех членов ряда. Промежуточные вычисления достаточно проводить с точностью до 0,00001. При этом погрешность промежуточных вычислений 
составит 0,00003, а общая погрешность 
Таким образом
Пример 2. Вычислить приближенно интеграл
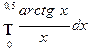
с точностью до 0,001.
Воспользуемся формулой (2.26) для разложения в степенной ряд функций 
и запишем разложение в степенной ряд подынтегральной функции
Этот ряд равномерно сходится на отрезке 
и поэтому можно почленно интегрировать
Т.к. ряд знакочередующийся, то
При 
поэтому 
и для вычисления ряда достаточно с заданной точностью взять первые три члена ряда. Промежуточные вычисления выполняем с точностью до четырех знаков. Итак
.
б) Рассмотрим задачу Коши Для дифференциального уравнения, например, первого
порядка
(2.29)
(2.30)
Предположим, что задача имеет решение и её решение представлено в виде ряда Тейлора
Значение 
находим из начального условия (2.30) 
. Значение 
найдем используя дифференциальное уравнение (2.29): 
.
Продифференцируем по х обе части дифференциального уравнения (2.29)
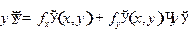(2.31)
Подставляя значение 
в правую часть, найдем:
Дифференцируя уравнение (2.31) ещё раз, найдем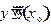 
и т.д. Обычно редко удаётся установит формулу общего члена, поэтому ограничиваются несколькими первыми членами ряда.
Пример 3. Найти решение дифференциального уравнения
удовлетворяющее начальному условию 
.
Будем искать решение этой задачи Коши в виде ряда Маклорена
Из начального условия имеем, что 
а из дифференциального уравнения находим 
Продифференцируем обе части уравнения
Отсюда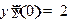 
. Продифференцируем, получившееся уравнение, ещё раз
Отсюда находим 
. Вычисляя первые коэффициенты степенного ряда, имеем 
Из этого часто делают вывод, что все коэффициенты степенного ряда равны 2. Однако этот вывод ошибочен. Действительно
Если дифференциальное уравнение является линейным, то решение задачи Коши удобно находить в виде степенного ряда с неопределёнными коэффициентами. Подставляя ряд в дифференциальное уравнение и приравнивая коэффициенты при одинаковых степенях Х в обеих частях равенства, получим бесконечную систему для определения этих коэффициентов. Решая систему, найдем коэффициенты.
Пример 5. Найти решение уравнения.
(2.32)
удовлетворяющее начальным условием
(2.33)
Решение задачи Коши будем искать в виде ряда
используя начальное условия, находим 
:
Вычислим вторую производную и подставим в уравнение
Приравниваем в обеих частях равенства коэффициенты при одинаковых степенях х:
Запишем четыре первых, отличных от нуля, члена разложения в степенной ряд решения задачи Коши
Пример 4. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения дифференциального уравнения
удовлетворяющего начальному условию 
Решение будем искать в виде ряда Тейлора в окрестности точки 
Из начального условия находим 
а из дифференциального уравнения 
Дифференцируя обе части уравнения
находим 
Ещё раз продифференцируем обе части уравнения
Отсюда 
Дифференцируя ещё раз обе части уравнения
находим 
Таким образом, имеем
,
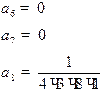Далее получим 
Запишем решение задачи (2.32), (2.33) в виде степенного ряда
С помощью признака Даламбера можно проверить, что этот ряд сходится при всех значениях х, поэтому он является решением задачи (2.32), (2.33).
III. РЯДЫФУРЬЕ.
1. РЯДЫФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 
.
Функциональный ряд вида
(3.1)
называется тригонометрическим рядом. Постоянные 
называются коэффициентами тригонометрического ряда. Если ряд (3.1) сходится, то его сумма является периодической функцией 
с периодом , т.е. 
.
Коэффициенты определяемые по формулам
(3.2)
называются коэффициентами Фурье функции , а тригонометрический ряд (3.1) называется рядом Фурье функции 
Теорема 1. (признак Дирихле) Если периодическая функция 
с периодом является кусочно – монотонная на отрезке 
, то ряд Фурье, построенный для этой функции сходится во всех точках. Сумма полученного ряда 
равна значению функции во всех точках непрерывности функции. В точках разрыва функции сумма ряда равняется среднему арифметическому пределов функции справа и слева, т.е., если 
- точка разрыва функции , то
Теорема 1 дает достаточное условие поточной сходимости ряда Фурье. Следующая ниже теорема определяет достаточное условие равномерной сходимости ряда Фурье.
Теорема 2. Если функция с периодом непрерывна на всей числовой оси и имеем кусочно – непрерывную производную на периоде, то её ряд Фурье равномерно сходится к ней.
Пример 1. Периодическая функция с периодом определена следующим образом:
.
Разложить функцию в ряд Фурье.
Функция - ограниченная и монотонная на периоде (см. рис. 1) следовательно, она допускает разложение в ряд Фурье.
Вычислим коэффициент 
:
Коэффициенты 
будем вычислять, используя формулу интегрирования по частям
При разложении функций в ряд Фурье часто будет использоваться тригонометрические формулы
Запишем разложение в ряд Фурье функции
В точках разрыва функции , т.е. в точках 
, сумма ряда равна 0.
Замечание. Ниже в п.2 будет показано, что для нечётной функции коэффициенты 
равны 0, т.е. интегралы можно было бы и не вычислять.
Отметим следующие свойства - периодической функции 
:
Интеграл от периодической функции по любому отрезку, длинна которого равна периоду, имеет одно и тоже значение.
В частности, если функция имеет период , то при любом 
.
Если функция имеет период , то функции 
также имеет период , и поэтому коэффициенты ряда Фурье можно вычислять по формулам:
(3.3)
Пример 2. Периодическая функция с периодом определена следующим образом:
.
Разложить функцию в ряд Фурье.
Функция является кусочно – монотонной и ограничённой на периоде (рис.2), поэтому её можно разложить в ряд Фурье.
Воспользуемся формулой (3.3) при 
Таким образом, Ряд Фурье будет иметь вид
В точках разрыва функции сумма ряда равна среднему арифметическому её пределов слева исправа, т.е. в данном случае .
- РЯДЫФУРЬЕ ДЛЯ ЧЁТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ.
Если функция является четной или нечетной, то формулы для вычисления коэффициентов ряда Фурье упрощается.
Если - четная функция 
то коэффициенты вычисляются по формулам
поэтому
Получено разложение функции в ряд Фурье по косинусам.
Если нечетная функция 
, то коэффициенты вычисляются по формулам
разложение имеет вид
и называется разложением по синысам.
Пример 1. Периодическая функция с периодом определена следующим образом
Разложить функцию в ряд Фурье. Функция (см. рис. 3) является ограниченной, непрерывной на всей числовой оси и имеет кусочно – непрерывную производную на периоде, поэтому ряд Фурье для этой функции будет равномерно сходится к ней на всей числовой оси.
Так как функция является четной, то 
.
Вычислим коэффициенты 
Если n-четное, т.е. 
то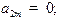 
если n-нечетное, т.е. 
то 
Запишеш разложение в ряд Фурье для функции :
Ряд равномерно сходится к функции на всей числовой оси.
- РЯД ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2l.
Если функция имеет период 2l, то её ряд Фурье имеет вид:
Коэффициенты 
вычисляются по формулам:
Если функция - четная то формулы для вычисления коэффициентов упрощяются
Если функция - нечётная 
то коэффициенты можно вычислить по формулам:
Пример 1. Разложить в ряд Фурье функция 
в интервале (-2;2).
Функция не является ни четной, ни нечетной. Рассмотрим функцию 
Функция является непрерывной и ограниченной на периоде, поэтому допускает разложение в ряде Фурье. Эта функция является нечетной поэтому разложение в ряд Фурье функции 
будет содержать только синусы.
Найдём коэффициенты разложения в ряд Фурье функции 
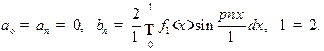
Разложение в ряд фурье функции будет иметь вид
Теперь запишем разложение в ряд Фурье функции 
:
Полученная формула имеет место при всех значениях 
a ряд, стоящий справа, сходится при всех значениях 
к функции, график которой изображен на рис.4. сплошной линией.
Функция , заданная на интервале 
, может быть разложена в ряд Фурье бесконечным числом способов в зависимости от того, как настроено ее продолжение на интервале 
. Если на интервал продолжить функцию четным образом, то получим разложение по косинусам; если на интервал продолжить функцию нечетным образом, то получим разложение по синусам.
Пример 2. Разложить в ряд Фурье по косинусам функцию, график которой изображен на рис.5.
Эта функция на полупериоде задаётся следуюющим образом:
Продолжим функцию на интервал (-3; 0) чётным образом, а затем периодически на всю числовую ось. Полученная функция будет непрерывна на всей числовой оси, вычислим коэффициенты Фурье.
Запишем разложение функции в ряд Фурье:
Ряд равномерно сходится на всей числовой оси.