
Тогда

в) 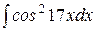
Решение
Используем формулу, позволяющую понизить степень тригонометри-ческой функции

Тогда получаем

г) 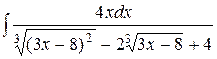
Решение


Так как подынтегральная функция является неправильной рациональной дробью, то разделим числитель на знаменатель:

Таким образом, получаем



П р и м е р 2. Вычислить площадь фигуры, ограниченной линиями 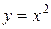 ,
, 

Решение. Изобразим фигуру, площадь которой необходимо вычислить:
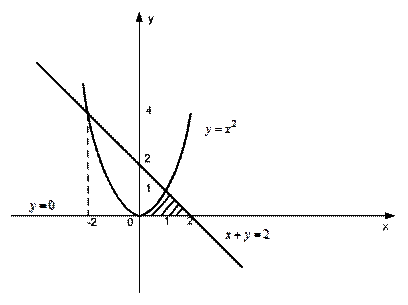
Координаты точек пересечения параболы 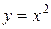 и прямой
и прямой  найдем из решения системы
найдем из решения системы  Откуда получаем (
Откуда получаем ( ) и (
) и ( ) – координаты точек пересечения. Исходя из геометрического смысла определенного интеграла, находим
) – координаты точек пересечения. Исходя из геометрического смысла определенного интеграла, находим


 =
=  (ед.2).
(ед.2).
П р и м е р 3. Вычислить длину дуги данной линии

Решение. Воспользуемся формулой

Находим подынтегральную функцию:



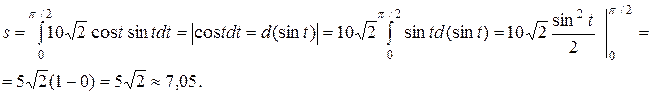
П р и м е р 4
а) Найти общее решение уравнения
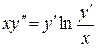 (1)
(1)
Решение. Данное уравнение относится к уравнениям вида  Понизив его порядок с помощью подстановки
Понизив его порядок с помощью подстановки  где
где 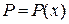 . Тогда
. Тогда  . Подставив в уравнение (1) вместо
. Подставив в уравнение (1) вместо  и
и 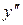 их выражения, получим
их выражения, получим
 (2)
(2)
Это однородное уравнение первого порядка относительно функции  . Уравнение (2) решим с помощью подстановки
. Уравнение (2) решим с помощью подстановки  Подставив это в уравнение (2), получим
Подставив это в уравнение (2), получим


Разделив переменные и проинтегрировав, получим


 ,
,
 ,
,

 .
.
Проинтегрировав, получим

б) Найти общее решение уравнения
 . (3)
. (3)
Решение. Данное дифференциальное уравнение второго порядка, допускающее понижение порядка, относится к уравнениям вида  Порядок такого уравнения понижается подстановкой
Порядок такого уравнения понижается подстановкой  , где
, где  Тогда
Тогда

Подставляя вместо  и
и 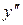 их выражения в уравнение (3), получим
их выражения в уравнение (3), получим
 или
или
 – линейное дифференциальное уравнение первого порядка относительно искомой функции
– линейное дифференциальное уравнение первого порядка относительно искомой функции 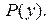
Решаем подстановкой 
 ,
,
 . (4)
. (4)
Функцию  выберем так, чтобы коэффициент при
выберем так, чтобы коэффициент при  был равен нулю.
был равен нулю.
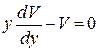 или
или 

Подставляя  в уравнение (4), получим
в уравнение (4), получим

 .
.
Тогда  или
или

Разделив переменные и проинтегрировав, получим

 – общий интеграл данного уравнения при
– общий интеграл данного уравнения при  Если
Если  т.е.
т.е.  то
то 
Ответ: 
 .
.
П р и м е р 5. Найти частное решение дифференциального уравнения
 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 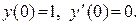
Решение. Общее решение данного уравнения состоит из суммы общего решения  соответствующего однородного уравнения и частного решения
соответствующего однородного уравнения и частного решения  неоднородного уравнения, т.е.
неоднородного уравнения, т.е. 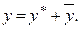
Решим сначала однородное уравнение
 .
.
Составим и решим характеристическое уравнение
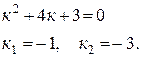
Так как корни характеристического уравнения действительные и разные, то общее решение  будет иметь вид
будет иметь вид
 .
.
Частное решение неоднородного уравнения будем искать в виде  .
.
В нашем случае 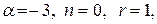 так как
так как 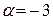 встречается один раз среди корней характеристического уравнения.
встречается один раз среди корней характеристического уравнения.
Итак,  , где
, где  это многочлен нулевой степени.
это многочлен нулевой степени.
(Если  то
то  при
при 
 и т.д.).
и т.д.).
Чтобы найти коэффициент А, найдем 
 и подставим в первоначальное уравнение.
и подставим в первоначальное уравнение.
 ;
;
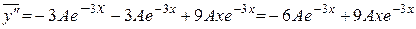 .
.
 .
.
Приведя подобные и сократив на  , получим
, получим
 откуда
откуда 
и частное решение имеет вид  .
.
Общее решение данного уравнения:

Найдем  и поставим начальные условия, откуда найдем
и поставим начальные условия, откуда найдем  и
и  .
.

 откуда
откуда  .
.
И частное решение будет иметь вид

П р и м е р 6. Расставить пределы интегрирования в двойном интеграле  в том и другом порядке, если область
в том и другом порядке, если область  задана линиями
задана линиями  и вычислить площадь этой области.
и вычислить площадь этой области.
Решение. Строим область  :
:
  |
Площадь плоской области  с помощью двойного интеграла вычисляется по формуле
с помощью двойного интеграла вычисляется по формуле
 .
.
Расставим пределы интегрирования в том и другом порядке. Переменная  изменяется от 0 до 1, в это время
изменяется от 0 до 1, в это время  изменяется от прямой
изменяется от прямой 
 до параболы
до параболы  , так как прямая, параллельная оси ОУ, пересекает сначала прямую
, так как прямая, параллельная оси ОУ, пересекает сначала прямую 
 (нижний предел), а затем параболу
(нижний предел), а затем параболу  (верхний предел). При изменении порядка интегрирования область
(верхний предел). При изменении порядка интегрирования область  придется разбить на две области
придется разбить на две области  1 и
1 и  2 прямой, параллельной оси
2 прямой, параллельной оси 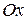 , так как правая часть контура области
, так как правая часть контура области  состоит из двух линий, определяемых разными уравнениями
состоит из двух линий, определяемых разными уравнениями  и
и 
Следовательно,

 (кв.ед.)
(кв.ед.)
П р и м е р 7. Вычислить криволинейный интеграл  ,
,
где АВ–дуга параболы  от т.А(
от т.А( ) до т.В (
) до т.В ( ).
).
Решение. Изобразим кривую, вдоль которой ведется интегрирование:

Вычисление криволинейного интеграла  сведем к вычислению определенного интеграла по формуле
сведем к вычислению определенного интеграла по формуле
 =
= 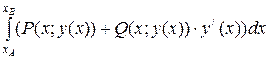 .
.
Так как АВ–дуга параболы, заданной уравнением  от т.А(
от т.А( ) до т.В (
) до т.В ( ), то
), то  , а переменная
, а переменная  меняется в пределах от 1 до 2. Следовательно,
меняется в пределах от 1 до 2. Следовательно,
 =
= 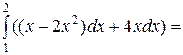

 =
=  =
= 


В О П Р О С Ы для подготовки к экзамену