Вихревое движение широко распространено как в природе, так и вразного рода технических устройствах. Поэтому изучение его закономерностей представляет несомненный практический интерес. Вращательное движение жидких частиц характеризуется вихрем скорости [35]
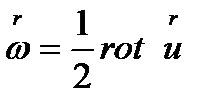(2.34)
Это означает, что в каждой точке пространства вращение жидких частиц может быть охарактеризовано этим вектором. Его модуль
(2.35)
Движение, при котором величина вихря скорости не равна нулю, т.е. 
, называют вихревым. При условии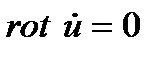 
движение безвихревое либо потенциальное.
Кинематические понятия для вихревого движения можно получить по аналогии с общими понятиями кинематики. В основу кинематики вихревого движения положено представление о вихревой линии, которое аналогично понятию линии тока. Вихревой называется линия, в каждой точке которой в данный момент времени вектор вихря скорости совпадает с касательной (рисунок 2.1). Другими словами, вихревая линия это мгновенная ось вращения частиц жидкости, которые в данный момент времени расположены на ней. По аналогии с дифференциальным уравнением линии тока можно записать
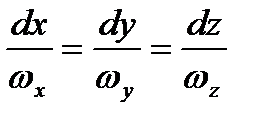(2.36)
Вихревая трубка аналог трубки (поверхности) тока. Это поверхность, образованная вихревыми линиями, проведенными через все точки бесконечно малого замкнутого контура. Вихревая нить аналог струйки это жидкость, заключенная в вихревой трубке. Если вихревая трубка имеет конечные размеры, то частицы, заполняющие ее и находящиеся во вращательном движении, образуют вихревой шнур.
|
Рисунок 22 – Вихревой шнур
Понятие интенсивности вихря достаточно абстрактно и вводится чисто математически. Напомним, что потоком векторного поля называют интеграл вида
(2.37)
Поскольку вихрь скорости (ротор) есть вектор, то вместо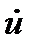 
можно подставить 
, что и приводит нас к понятию интенсивности вихря, т.е. интенсивность вихря это поток вектора вихря
(2.38)
Можно использовать и другую форму записи: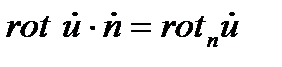 
;
(2.39)
Имея в виду, что 
, можем записать
(2.40)
Воспользуемся формулой Гаусса-Остроградского и перейдем от интеграла по поверхности к интегралу по объему. Имеем:
Раскроем выражение, стоящее под знаком интеграла, имея в виду, что проекции вектора вихря имеют вид:
;
;
.
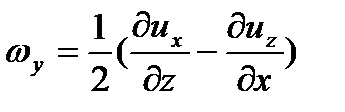Имеем
Следовательно, можно записать
(2.41)
Заметим, что это выражение по структуре напоминает уравнение неразрывности.
Применим (2.41) к вихревому шнуру (рисунок 23).
Рисунок 23 –Проекция скоростей
На боковой поверхности 
, так как 
направлен по касательной к поверхности. Поэтому можем записать
;
.
Если допустить, что в пределах сечения 
то
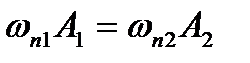(2.42)
Либо в общем случае
(2.43)
т.е. это своеобразное «уравнение неразрывности». Полученный результат носит название теоремы Гельмгольца о вихрях, которую можно сформулировать следующим образом: интенсивность вихревого шнура навсей его протяженности остается постоянной. Из выражения (2.13) следует и другой весьма важный вывод, сделанный Г.Гельмгольцем в 1855г. в работе «Об интегралах уравнений, соответствующих вихревым движениям». Так как произведение 
остается неизменным, то уменьшение площади сечения шнура должно приводить к увеличению угловой скорости вращения частиц. При 
, 
, что физически невозможно. Следовательно, вихрь не может зарождаться либо оканчиваться в толще жидкости. Окончательно развившись, он должен замкнуться либо на твердую поверхность, либо сам на себя, т.е. образовать вихревое кольцо [38].
Понятие об интенсивности является весьма важным, но, к сожалению, непосредственное определение этой величины экспериментальным путем связано с непреодолимыми трудностями. Кроме того, если пытаться распространить это понятие на вихри конечных размеров, то по аналогии со средней скоростью пришлось бы вводить понятие о средней угловой скорости, что связано с определенными трудностями чисто математического характера. Поэтому гидромеханика избрала другой путь, заменив это понятие другим, более удобным для целей практики. К рассмотрению этого понятия, называемого циркуляцией скорости, мы и приступим.
Для введения понятия о циркуляции скорости в настоящем пособии используется методика Н.Я.Фабриканта. Несомненным преимуществом ее является то, что в отличие от других она позволяет ввести понятие циркуляции не чисто математически, а исходя из достаточно простых и ясных физических предпосылок.
Рассмотрим крыловой профиль, находящийся в потоке газа (воздуха). Как известно, на профиль в этом случае будет действовать подъемная сила (рисунок 24). Физически наличие этой силы можно объяснить лишь тем, что давление под профилем (
) больше, а давление над профилем (
) меньше, чем давление на каком-то удалении от него, которое мы обозначим 
Это позволяет утверждать, что под крыловым профилем скорость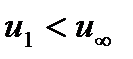 
, а над ним 
. В данном случае 
скорость невозмущенного потока.
Рисунок 24 – Профиль крыла
Вычтем теперь из скоростей 
и 
скорость 
, т.е. 
и 
. Это действие приводит нас к понятию потока возмущения, т.е. движения, которое возникает в среде из-за того, что в нее внесено инородное тело, т.е., по существу, это реакция потока, обусловленная в рассматриваемом случае тем, что в ней появился крыловой профиль. Установим теперь направление потоков возмущения. Под профилем 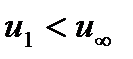, и он направлен против скорости 
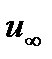, над профилем - наоборот. В результате появляется циркуляционный поток, направленный по часовой стрелке, как это показано на рисунке 24. Теперь необходимо охарактеризовать этот поток количественно. Именно с этой целью вводится понятие циркуляции скорости по замкнутому контуру.
Рассмотрим замкнутый контур C, показанный на рисунке 25. Пусть в произвольной точке M скорость равна 
. Составим скалярное произведение 
, где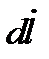 
направленный элемент дуги.
|
Рисунок 25 – Замкнутый контур
Циркуляцией скорости называют контурный интеграл вида
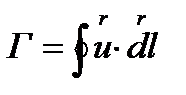(2.44)
Обратим внимание на структуру этого соотношения. Оно построено аналогично выражению для работы, поэтому иногда говорят, что циркуляция - это своеобразная «работа» вектора скорости. Имея в виду, что 
и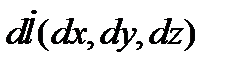 
, по правилу скалярного произведения получим
(2.45)
Для плоского течения:
(2.46)
В конце предыдущего раздела утверждалось, что понятие циркуляции является более удобным, чем интенсивность вихря. Действительно, из (2.46) следует, что для определения циркуляции достаточно знать проекции скорости, нахождение которых не связано с существенными трудностями. Однако остается пока открытым вопрос о том, существует ли связь между циркуляцией и интенсивностью вихря. Ответ получим из теоремы Стокса.
В движущейся жидкости рассматриваем вихревое поле и выделяем в нем малый замкнутый контур со сторонами dx и dy (рисунок 26).
|
Рисунок 26 – Вихревое поле
Пусть в начале координат скорости будут 
и 
. Запишем выражение для элементарной циркуляции по этому контуру, имея в виду, что поток двумерный: 
.
Рассмотрим контур OABC. Если вдоль OA скорость , то вдоль CB ее приращение составит 
, и аналогично вдоль AB - 
. Это следует из выражения для полного дифференциала скорости, например,
.
Запишем теперь выражение для элементарной циркуляции вдоль контура OABCO. Имеем:
Раскрывая скобки и выполнив сокращения, получаем
Из чего следует, что циркуляция по бесконечно малому замкнутому контуру равна интенсивности вихря, пронизывающего этот контур.
Этот вывод легко обобщить и на случай произвольной кривой конечных размеров [39].
Таким образом, можем записать:
(2.47)
Полученная зависимость (2.47) есть формула Стокса, показывающая, что циркуляция по произвольному контуру равна сумме интенсивностей (напряжений) вихрей, пронизывающих поверхность, натянутую на контур.