Как уже отмечалось, условием потенциальности движения является равенство нулю вихря скорости, т.е.  Физически это означает, что движение жидкости происходит без вращения частиц. Как будет показано, потенциальное движение играет исключительно важную роль в механике жидкости.
Физически это означает, что движение жидкости происходит без вращения частиц. Как будет показано, потенциальное движение играет исключительно важную роль в механике жидкости.
Сущность теоремы Стокса, по существу, сводится к утверждению о равенстве числовых значений интенсивности вихря и циркуляции, т.е. 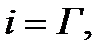 либо
либо

С другой стороны, для потенциального потока по его определению  т.е. в потенциальном поле циркуляция по замкнутому контуру равна нулю.
т.е. в потенциальном поле циркуляция по замкнутому контуру равна нулю.
Запишем выражения для проекций угловых скоростей.

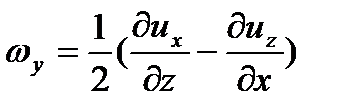

Из сказанного выше следует, что для безвихревого (потенциального) движения  . Следовательно, в этом случае
. Следовательно, в этом случае
 ;
;  ;
;  (2.48)
(2.48)
Эти соотношения позволяют существенным образом упростить вычисления компонент скорости  ,
,  и
и  .
.
Рассмотрим выражение
 (2.48.1)
(2.48.1)
Оно построено аналогично известному из механики твердого тела выражению для элементарной работы. Зададимся вопросом, в каком случае (2.48.1) является полным дифференциалом. Напомним, что если выражение для работы является полным дифференциалом, то силы называются консервативными или имеющими потенциал [40]. Ответ на поставленный вопрос был дан Алесисом Клодом Клеро,который показал, что выражение типа (2.48.1) является полным дифференциалом, если обеспечивается равенство накрест взятых производных. Соотношения (2.48) как раз и удовлетворяют этому требованию, т.е. взятые накрест производные в (2.48.1) дают соотношения (2.41). Таким образом, при потенциальном движении выражение (а) является полным дифференциалом какой-то функции, и
 (2.49)
(2.49)
С другой стороны, по общему правилу полный дифференциал может быть представлен как
 (2.50)
(2.50)
Сопоставляя (2.49) и (2.50), получаем
 ;
;  ;
;  (2.51)
(2.51)
По предложению Гельмгольца функцию называют потенциалом скорости.
Таким образом, всякому движению жидкости, происходящему без вращения частиц, соответствует свой потенциал скорости. Справедливо и обратное утверждение: если существует потенциал скорости, то движение происходит без вращения частиц.
Соотношения (2.51) можно получить и другим путем. Поскольку разные подходы к одному и тому же вопросу способствуют углубленному его пониманию, то получим эти же соотношения, используя другую методику.
Как уже отмечалось, условием потенциальности является  С другой стороны, как показано при рассмотрении операций второго порядка, операция ротора над градиентом какой-то скалярной функции тождественно равна нулю, т.е.
С другой стороны, как показано при рассмотрении операций второго порядка, операция ротора над градиентом какой-то скалярной функции тождественно равна нулю, т.е.

Сопоставляя эти соотношения, можем записать
 (2.52)
(2.52)
Это означает, что вектор скорости можно рассматривать как градиент какой-то скалярной функции. Раскроем значения  и
и  . Имеем
. Имеем
 ;
;
 .
.
Откуда, учитывая (2.52), получаем
 ;
;  ;
;  ,
,
т.е. вновь приходим к соотношениям (2.51).
Пока что остается открытым вопрос о необходимости и целесообразности введения понятия о потенциале скорости. Чтобы разобраться в этом, следует иметь в виду, что к числу центральных задач гидромеханики относится определение сил, действующих на тела, обтекаемые потоками жидкости либо газа. Решение этих задач непосредственно связано с необходимостью расчета поля скоростей, т.е. определением проекций скоростей( ,
,  ,
,  ) в каждой его точке. Из выражений (2.4) непосредственно следует, что все три компоненты скорости могут быть определены, если известна лишь одна величина - потенциал скорости. Таким образом, знание потенциала скорости существенно упрощает расчет поля скорости. Однако немедленно возникает следующая проблема - как же найти потенциал скорости течения. Чтобы решить ее, необходимо прежде всего уяснить некоторые свойства, присущие потенциалу.
) в каждой его точке. Из выражений (2.4) непосредственно следует, что все три компоненты скорости могут быть определены, если известна лишь одна величина - потенциал скорости. Таким образом, знание потенциала скорости существенно упрощает расчет поля скорости. Однако немедленно возникает следующая проблема - как же найти потенциал скорости течения. Чтобы решить ее, необходимо прежде всего уяснить некоторые свойства, присущие потенциалу.
Операция дивергенции над градиентом скалярной функции приводит к оператору Лапласа. Если в качестве скалярной функции использовать потенциал скорости, то можно записать
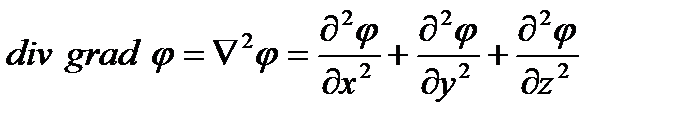 (2.53)
(2.53)
Для несжимаемой жидкости 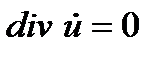 , а
, а  . Таким образом
. Таким образом
 (2.54)
(2.54)
либо
 (2.55)
(2.55)
Выражения (2.54) и (2.55) носят название уравнения Лапласа. Таким образом, для нахождения потенциала скорости необходимо проинтегрировать уравнение Лапласа. Любая функция, удовлетворяющая этому уравнению, носит название гармонической. Следовательно, потенциал скорости является гармонической функцией. Как любое дифференциальное уравнение, уравнение Лапласа имеет бесчисленное множество решений, поэтому для того, чтобы однозначно определить потенциал скорости, необходимо задать граничные условия. Для задач, связанных с обтеканием тел, так называемых внешних задач гидромеханики, такими условиями являются  и
и  .
.
Первое условие характеризует безотрывность течения (равенство нулю нормальной компоненты скорости). Второе - показывает, что вдали от тела распределение скоростей известно.
Поверхности (либо линии для двумерных потоков), в каждой точке которых  , называются эквипотенциальными.
, называются эквипотенциальными.
Рассмотрим плоский (двумерный) поток. Выделим в нем произвольную кривую (рисунок 3.1) и запишем выражение для циркуляции вдоль этой кривой
 (2.56)
(2.56)

|
т.е. циркуляция вдоль кривой не зависит от ее формы, а определяется лишь разностью потенциалов в ее конечных точках. Если кривая замкнута, то очевидно, что  и
и  , т.е. циркуляция по замкнутому контуру в потенциальном поле равна нулю.
, т.е. циркуляция по замкнутому контуру в потенциальном поле равна нулю.
Рисунок 27 – Двумерный поток
В практических задачах гидромеханики двумерных потоков широчайшее применение находит понятие о функции тока. Рассмотрим двумерный поток и ограничимся несжимаемой жидкостью.
Как было показано, дифференциальное уравнение линии тока имеет вид

либо
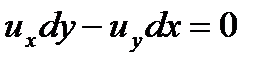 (2.57)
(2.57)
Запишем уравнение неразрывности для этого случая, которое будет иметь вид
 (2.58)
(2.58)
Аналогично тому, как это делалось при рассмотрении потенциала скорости, поставим вопрос об условиях необходимых и достаточных для того, чтобы выражение (2.57) являлось полным дифференциалом какой-то скалярной функции. Применим к (2.58) условия Клеро (равенство взятых накрест производных). Имеем:
 и
и 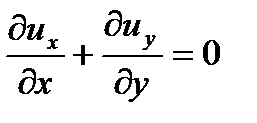 .
.
Но это есть не что иное, как уравнение неразрывности (2.58) для плоского потока, которое удовлетворяется всегда, если только движение существует. Следовательно, можно записать:
 (2.59)
(2.59)
где  носит название функции тока. С другой стороны, поскольку, как показано выше,
носит название функции тока. С другой стороны, поскольку, как показано выше,  является полным дифференциалом, то можно записать:
является полным дифференциалом, то можно записать:
 (2.60)
(2.60)
Сопоставляя (2.59) и (2.60), получаем
 (2.61)
(2.61)
Из чего следует, что если функция тока течения известна, то можно определить компоненты скорости в любой точке пространства. Сопоставляя (2.57) и (2.59) приходим к выводу, что если частица движется вдоль линии тока, то функция тока остается постоянной (при  ,
,  и (2.52) превращается в (2.57)). Проверим теперь, является ли функция тока гармонической функцией, т.е. удовлетворяет ли она уравнению Лапласа.
и (2.52) превращается в (2.57)). Проверим теперь, является ли функция тока гармонической функцией, т.е. удовлетворяет ли она уравнению Лапласа.
Для плоского потенциального течения  , но
, но 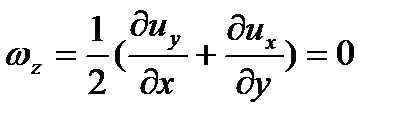 ,
,
Откуда

Из (2.61)  и
и  , следовательно
, следовательно

откуда

Таким образом, функция тока, как и потенциал скорости, является гармонической функцией. И еще одно важное обстоятельство. Если потенциал скорости существует только в потенциальном потоке, то функция тока этим условием не ограничена. Это объясняется тем, что уравнение неразрывности, которое используется для получения этого понятия, справедливо как для вихревого, так и для безвихревого движений.
Установим гидромеханический смысл функции тока, для чего проведем две достаточно близко расположенные линии тока (рисунок 28). Вычислим объемный расход жидкости, протекающий между ними, для чего разложим вектор скорости частицы  на две составляющие
на две составляющие  и
и  , что позволит представить расход как сумму
, что позволит представить расход как сумму  , при этом
, при этом  и
и  (рисунок 28).
(рисунок 28).

Рисунок 28 – Линии тока

 (2.62)
(2.62)
т.е. разность значений функций тока на двух смежных линиях тока равна объемному расходу между ними.
Связь между этими параметрами может быть легко установлена, если записать полученные выше выражения для проекций скоростей
 ;
;  ;
;
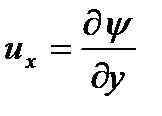 ;
; 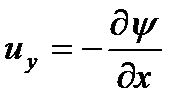 ,
,
откуда
 (2.63)
(2.63)
Эти соотношения играют чрезвычайно важную роль в механике жидкости и носят название соотношений Коши-Римана. Более подробно они будут рассмотрены ниже. Пока же ограничимся тем, что перемножим их. Это дает
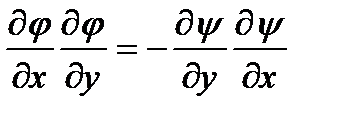 (2.64)
(2.64)
Из математики известно, что выражения типа (2.64) свидетельствуют о взаимной ортогональности кривых. Следовательно, линии тока и эквипотенциальные линии образуют сетку взаимно ортогональных кривых, которая носит название гидродинамической сетки движения. Примерный ее вид показан на рисунке 29.

Рисунок 29 – Гидродинамическая сетка
Как уже отмечалось, для нахождения потенциала скорости необходимо проинтегрировать уравнение Лапласа при заданных граничных условиях. Задача эта достаточно сложна. Поэтому в теории потенциальных течений особый интерес представляют случаи, которые дают точные значения функций тока и потенциала скорости без интегрирования уравнения Лапласа. Общая идея такого подхода сводится к следующему: задаются какой-то функцией, которая заведомо удовлетворяет уравнению Лапласа и выясняют, что представляет собой гидродинамическая сетка движения. Эту методику рассмотрим на ряде простейших примеров.
Рассмотрим линейный случай. Пусть выражение для потенциала скорости имеет вид  , где a и b - действительные числа.
, где a и b - действительные числа.
Найдем компоненты скорости. Имеем
 и
и  .
.
Вторые производные равны нулю, т.е. уравнение Лапласа удовлетворяется. Так как  и
и 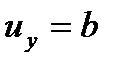 , то из этого следует, что поток движется с постоянной скоростью
, то из этого следует, что поток движется с постоянной скоростью

Выясним, что представляют собой линии тока. Дифференциальное уравнение линий тока
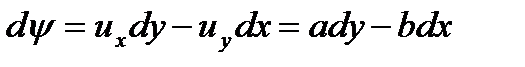
И после интегрирования
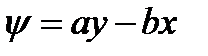 (2.65)
(2.65)
Приравнивая (2.58) какой-то постоянной, получаем семейство линий тока - параллельных прямых (рисунок 30), наклоненных к оси под углом  . Действительно, для линии тока можем записать:
. Действительно, для линии тока можем записать:

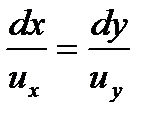 ;
;  .
.

|
Рисунок 30 – Прямолинейная сетка
При потенциале скорости, заданный выражением

где a - действительное число, определим линии тока этого течения.
Прежде всего проверим, удовлетворяет ли уравнению Лапласа.
Имеем
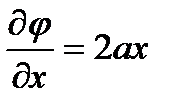 ;
;  ;
;  ;
; 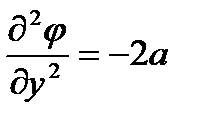 ;
; 
 ,
,
т.е. уравнение Лапласа удовлетворяется. Выясним, какое же движение описывается этой функцией, для чего установим вид функции тока.


Следовательно,  (произвольная постоянная в данном случае нас не интересует).
(произвольная постоянная в данном случае нас не интересует).
Для нахождения линии тока приравняем  какой-то постоянной величине
какой-то постоянной величине 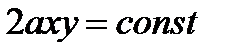 либо
либо  . Следовательно, линии тока - гиперболы, для которых оси x и y - асимптоты. На рисунке 31 показаны линии тока для верхней половины. Если считать, что оси координат являются твердыми стенками, то получим картину обтекания потоком прямого угла.
. Следовательно, линии тока - гиперболы, для которых оси x и y - асимптоты. На рисунке 31 показаны линии тока для верхней половины. Если считать, что оси координат являются твердыми стенками, то получим картину обтекания потоком прямого угла.

Рисунок 31 - Гипербола
Существует ряд простейших течений, для которых потенциалы скорости могут быть получены аналитическим путем. Эти течения играют заметную роль в гидромеханике, и поэтому их рассмотрение представляет несомненный интерес.
Рассмотримисточник (сток) на плоскости. Ограничимся плоской задачей [41].
Под источником (стоком) на плоскости понимают точку, из которой происходит истечение (либо втекание) жидкости.
Пусть точкаOна рисунке 32 представляет плоский источник, из которого, как из центра, проведем несколько концентрических окружностей. Запишем уравнение неразрывности для цилиндрической поверхности единичной высоты:
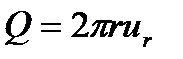
откуда
 (2.66)
(2.66)
В декартовой системе координат
 (2.67)
(2.67)

Рисунок 32 - Сток
В рассматриваемом случае удобней использовать цилиндрическую систему координат. Увязка систем может быть получена, исходя из рисунка 33.

Рисунок 33 – Координаты
Для цилиндрической системы [42]
 ;
;  (2.68)
(2.68)
Из (2.68) следует, что  не зависит от полярного угла, поэтому можно записать
не зависит от полярного угла, поэтому можно записать 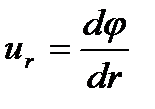 . Приравнивая это выражение (2.66), получим
. Приравнивая это выражение (2.66), получим  , откуда
, откуда  .
.
И после интегрирования
 (2.69)
(2.69)
Из (2.69) следует, что эквипотенциальные линии источника представляют собой окружности. Формулу (2.69) можно записать и в следующей форме
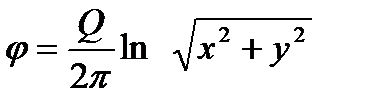 (2.70)
(2.70)
Для нахождения функции тока удобней использовать декартову систему координат. При этом (2.66) принимает вид:
 (2.71)
(2.71)
С другой стороны, из рисунка 33 следует:

Таким образом

Аналогично
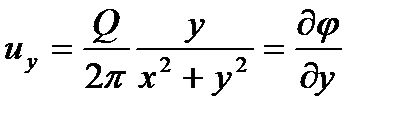
Дифференциальное уравнение функции тока
 (2.72)
(2.72)
Подстановка значений  и
и  в (2.72) дает
в (2.72) дает
 (2.73)
(2.73)
Выполним некоторые преобразования. Дифференциал от частного имеет вид
 , т.е.
, т.е.  .
.
Из знаменателя (2.73) выносим за скобки  , при этом
, при этом

Таким образом, (2.73) принимает вид

и

Но с другой стороны 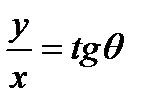 , т.е.
, т.е.  , и
, и
 (2.74)
(2.74)
В полярной системе координат (2.74) представляет собой семейство прямых, проходящих через начало координат. Для стока потенциал скорости и функция тока имеют те же выражения, но с противоположными знаками, т.е.
 и
и  (2.75)
(2.75)
Иногда Q называют мощностью (обильностью) источника.
Предположим, что имеются два потока с известными потенциалами скорости  и
и 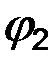 , удовлетворяющими уравнению Лапласа. Из теории линейных дифференциальных уравнений, к которым принадлежит и уравнение Лапласа, известно, что сумма частных решений этих уравнений также является их решением. Другими словами, это означает, что потенциал
, удовлетворяющими уравнению Лапласа. Из теории линейных дифференциальных уравнений, к которым принадлежит и уравнение Лапласа, известно, что сумма частных решений этих уравнений также является их решением. Другими словами, это означает, что потенциал 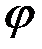 , образованный как
, образованный как  , также будет удовлетворять уравнению Лапласа, т.е. будет описывать какой-то новый поток, имеющий потенциал. Из этого следует, что можно получить новый поток путем сложения (наложения) уже известных. Следует обратить внимание на то, что собственно наложение потоков здесь не производится, а речь идет о сложении потенциалов скорости уже известных течений.
, также будет удовлетворять уравнению Лапласа, т.е. будет описывать какой-то новый поток, имеющий потенциал. Из этого следует, что можно получить новый поток путем сложения (наложения) уже известных. Следует обратить внимание на то, что собственно наложение потоков здесь не производится, а речь идет о сложении потенциалов скорости уже известных течений.
Скорость в каждой точке нового потока является суммой скоростей первоначальных потоков. Задача нахождения нового течения может быть решена как графически, так и аналитически.
Рассмотрим сначала графический метод. Общий подход сводится к следующему. Необходимо построить линии тока течений в одинаковом масштабе, что при достаточной густоте линий тока при пересечении дает фигуру, близкую к параллелограмму (рисунок 34).

|
Рисунок 34 – Графический метод
Отрезки AB и AD в каком-то масштабе представляют скорости течения, их результирующая определяется как диагональ параллелограмма (AC). Для построения такой сетки необходимо соблюсти следующее условие: расход между соседними линиями тока обоих течений должен быть одинаков.
В качестве примера рассмотрим картину течения, образующуюся при наложении плоского параллельного потока на сток(рисунок 35). Как следует из рисунка 35, частицы жидкости в новом течении будут двигаться по кривым, направленным к стоку.

Рисунок 35 – Гибридная сетка
Задача, как отмечалось выше, может быть решена и аналитически. В этом случае должны быть известныи 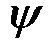 обоих течений.
обоих течений.
Выполним сложение источника и стока с одинаковыми расходами, симметрично расположенными относительно начала координат на расстоянии a (рисунок 36).
Потенциалы скорости: источника  ; стока -
; стока - 

Рисунок 36 – Источник и ток
Выбираем произвольную точку M с координатами x и y. Потенциал скорости в этой точке  т.е.
т.е.  . Выполним некоторые преобразования этого соотношения. Из треугольников MИx и MСx получаем:
. Выполним некоторые преобразования этого соотношения. Из треугольников MИx и MСx получаем:

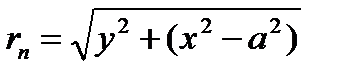
Следовательно, потенциал скорости нового течения
 (2.76)
(2.76)
Рассмотрим теперь картину, образующуюся при сближении источника и стока.Получаемое при сближении источника и стока течение называется диполем. Если предположить, что расстояние  , то
, то 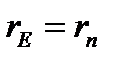 , и
, и 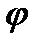 и
и  тождественно равны нулю. Поэтому рассмотрим другой предельный случай. Пусть при
тождественно равны нулю. Поэтому рассмотрим другой предельный случай. Пусть при  расход
расход  , но так, что произведение
, но так, что произведение  , где M носит название момента диполя. Таким образом,
, где M носит название момента диполя. Таким образом,
 (2.77)
(2.77)
Приэтомпотенциалскоростидиполя

Рассмотримпределэтогоотношения

Разберемся теперь в том, что представляет собой выражение, стоящее под знаком предела. Знаменатель можно рассматривать как приращение независимого переменного, а числитель - как соответствующее приращение функции. Действительно, рассмотрим функцию  . Придадим x значение
. Придадим x значение  и
и  . Если теперь из значения функции, соответствующей
. Если теперь из значения функции, соответствующей 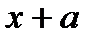 , вычесть ее значение при
, вычесть ее значение при  , то получим числитель. Разность значений независимого переменного
, то получим числитель. Разность значений независимого переменного 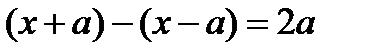 есть знаменатель. Таким образом, мы должны вычислить предел отношения приращения функции к приращению независимого переменного при стремлении последнего к нулю. Как известно, в математике такой предел называют производной функции, т.е.
есть знаменатель. Таким образом, мы должны вычислить предел отношения приращения функции к приращению независимого переменного при стремлении последнего к нулю. Как известно, в математике такой предел называют производной функции, т.е.

Дифференцирование легко выполняется методом подстановок. Пусть
 ;
; 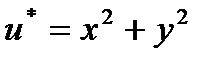 .
.
Тогда
 ;
;  ;
;  .
.
Имеем:
 ;
;  ,
,
т.е.
 .
.
Таким образом:
 (2.78)
(2.78)
Действуя аналогичным образом, можно показать, что
 (2.79)
(2.79)
Из чего следует, что линии тока и эквипотенциальные линии - окружности, касающиеся осей Ox и Oy в начале координат (рисунок 37).

Рисунок 37 – Сетка в виде окружностей
Действительно, придавая функции тока постоянные значения, получаем:

где
 ;
;
 ;
;
 ;
;
 ,
,
а это и есть уравнения окружностей с разными центрами.
Продолжим рассмотрение метода наложения потоков. Полученное течение, называемое диполем, на первый взгляд носит достаточно абстрактный характер. Однако, как будет показано ниже, такая точка зрения не совсем справедлива. Используя понятие диполя, можно получить весьма интересные и полезные для практических приложений результаты. Для подтверждения этого проанализируем течение, возникающее при наложении прямолинейного поступательного потока на диполь с центром, расположенным в начале координат. Прямолинейный поток движется вдоль оси Ox со скоростью, равной единице, т.е. 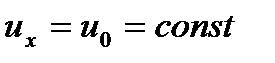 ;
;  .Потенциал скорости
.Потенциал скорости

и  с точностью до произвольной постоянной.
с точностью до произвольной постоянной.
Функция тока  и
и  . Если, как принято в условии,
. Если, как принято в условии,  , то
, то  и
и  . Примем для упрощения выкладок момент диполя
. Примем для упрощения выкладок момент диполя  , тогда
, тогда  и
и  . Складывая потенциалы и функции тока, получаем
. Складывая потенциалы и функции тока, получаем 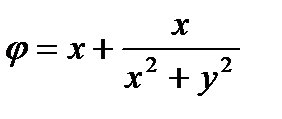 и
и  .
.
Найдем линии тока, для чего приравняем функцию тока постоянной:
 ,
,
откуда
 (2.80)
(2.80)
Из чего следует, что линии тока течения представляют семейство кривых третьего порядка. Найдем нулевую линию тока, т.е. линию, для которой  . Это дает два уравнения:
. Это дает два уравнения: 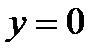 и
и  ,т.е. линия тока представляет собой ось x -ов и окружность единичного радиуса с центром в начале координат (рисунок 38). Это позволяет рассматривать окружность как твердую границу и течение вне ее, что приводит к задаче обтекания бесконечно длинного цилиндра.
,т.е. линия тока представляет собой ось x -ов и окружность единичного радиуса с центром в начале координат (рисунок 38). Это позволяет рассматривать окружность как твердую границу и течение вне ее, что приводит к задаче обтекания бесконечно длинного цилиндра.

Рисунок 38 – Обтекание цилиндра
Покажем, что на достаточно большом удалении от цилиндра скорость направлена вдоль оси x и равна  . Найдем проекции скоростей
. Найдем проекции скоростей  и
и 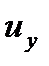 .
.
Имеем:
 ,
,
Откуда
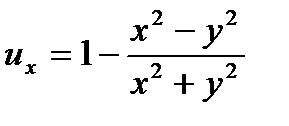 ;
;
аналогично
 .
.
Для дальнейшего удобно перейти к полярным координатам, имея в виду, что  и
и  . Подстановка этих значений в выражения для
. Подстановка этих значений в выражения для  и
и 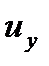 дает:
дает:
 (2.81)
(2.81)
 (2.82)
(2.82)
Перейдем к пределу. При  получаем
получаем  и
и  , т.е. то, что и требовалось доказать.
, т.е. то, что и требовалось доказать.
Точки B и A, показанные на рисунке 38, являются так называемыми особыми либо критическими точками, т.к. скорость в них обращается в нуль. Покажем, что это действительно так, для чего запишем выражение для потенциала скорости в полярных координатах:
 ;
;
 (2.83)
(2.83)
Найдем проекции скорости в произвольной точке на произвольной линии тока (рисунок 39). Имеем:
 ;
;
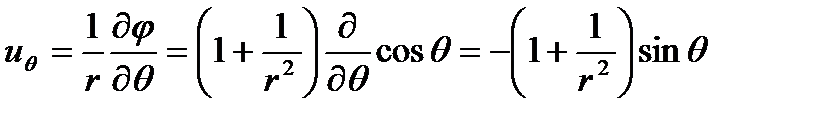 .
.

Рисунок 39 – Проекция скорости
На поверхности цилиндра  и
и  , т.е. обтекание безотрывно. Компонента
, т.е. обтекание безотрывно. Компонента  . В общем случае, когда
. В общем случае, когда  ,
,
 (2.84)
(2.84)
Знак «минус» указывает на то, что направление скорости на верхней половине цилиндра противоположно положительному направлению отсчета угла 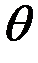 . В точках B и A(
. В точках B и A( 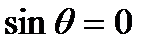 ) скорости равны нулю, т.е. действительно эти точки являются критическими.
) скорости равны нулю, т.е. действительно эти точки являются критическими.
Рассматриваемый ниже метод относится к числу наиболее эффективных способов анализа плоских потоков. Вернемся к полученным выше (см. 2.62) соотношениям Коши-Римана. Они показывают, что комплексная комбинация этих двух функций (т.е.  и
и  ) от действительных переменных x и y, т.е.
) от действительных переменных x и y, т.е.  , является аналитической функцией комплексного переменного
, является аналитической функцией комплексного переменного  . Другими словами, эти условия показывают, что существует функция комплексной переменной
. Другими словами, эти условия показывают, что существует функция комплексной переменной  либо просто W, вещественная и мнимая части которой
либо просто W, вещественная и мнимая части которой  и
и  соответственно, т.е.
соответственно, т.е.
 (либо
(либо  ).
).
Функция  называется аналитической в данной точке, если она дифференцируема как в самой точке, так и в некоторой ее окрестности. В гидромеханике функция
называется аналитической в данной точке, если она дифференцируема как в самой точке, так и в некоторой ее окрестности. В гидромеханике функция  называется комплексным потенциалом. Следует отметить, что теория аналитических функций является одной из наиболее разработанных ветвей классической математики [43].
называется комплексным потенциалом. Следует отметить, что теория аналитических функций является одной из наиболее разработанных ветвей классической математики [43].
Как показывается в теории функций комплексного переменного, производная от комплексного потенциала  по комплексному же переменному
по комплексному же переменному  имеет вид [44]:
имеет вид [44]:
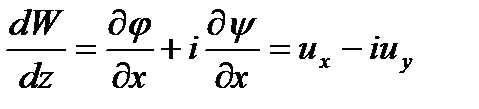 (2.85)
(2.85)
Это выражение называется комплексной скоростью. Модуль этой величины дает саму скорость, т.е.
 (2.86)
(2.86)
Рассмотрим некоторые примеры.
Пусть течение задано комплексным потенциалом  , где a - действительное число. Имея в виду, что
, где a - действительное число. Имея в виду, что  и
и  ,можно записать:
,можно записать:

Разделяя действительную и мнимую части, получаем:
 и
и  .
.
Этот поток рассмотрен выше. Обратим лишь внимание на то, что с помощью комплексного потенциала результат достигается более коротким путем.
Найдем комплексную скорость. Имеем:
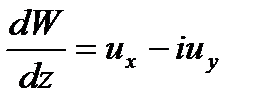 ;
;
 ;
;  ;
;
 ;
;
 ,
,
т.е. частицы движутся по гиперболическим линиям тока со скоростью  .
.
Геометрические преобразования, при которых величины углов между любыми двумя линиями, содержащимися в преобразуемой фигуре, не изменяются, называются конформными преобразованиями или отображениями. Широкое применение конформные отображения находят в гидромеханике. Обсудим лишь общую идею метода.
Рассмотрим две координатные сетки на плоскостях комплексных переменных  и
и  (рисунок 40).
(рисунок 40).

Рисунок 40 – ОтображениеА в В
В плоскости z имеется какая-то фигура (A), которую необходимо отобразить на плоскость 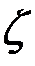 . Эта операция может быть выполнена при одном непременном условии: должно быть известно соотношение, устанавливающее связь
. Эта операция может быть выполнена при одном непременном условии: должно быть известно соотношение, устанавливающее связь 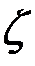 и z, т.е.
и z, т.е.  .Эта зависимость носит название отображающей функции. Предположим, что она нам известна. Тогда, задавшись какой-то произвольной точкой на контуре A, например 1, можно вычислить
.Эта зависимость носит название отображающей функции. Предположим, что она нам известна. Тогда, задавшись какой-то произвольной точкой на контуре A, например 1, можно вычислить  , и подставив это значение в отображающую функцию, найти значение
, и подставив это значение в отображающую функцию, найти значение  и соответствующую точку на плоскости
и соответствующую точку на плоскости 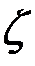 (1'). Повторив эти операции для точек 2, 3 и т.д., найдем 2', 3',.... В результате этих действий получим контур B на плоскости
(1'). Повторив эти операции для точек 2, 3 и т.д., найдем 2', 3',.... В результате этих действий получим контур B на плоскости 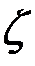 , т.е. контур A отобразился в контур B. Такое преобразование получило название конформного. В теории функций комплексного переменного доказывается, что модуль производной
, т.е. контур A отобразился в контур B. Такое преобразование получило название конформного. В теории функций комплексного переменного доказывается, что модуль производной  характеризует изменение линейных размеров области при преобразовании, а аргумент ее определяет угол поворота радиуса-вектора. При этом преобразование, осуществляемое аналитической функцией, сохраняет эти углы во всех точках, где производная отображающей функции отличается от нуля. Теперь вопрос может быть сформулирован таким образом: какие же практические преимущества можно получить, используя метод конформных отображений?
характеризует изменение линейных размеров области при преобразовании, а аргумент ее определяет угол поворота радиуса-вектора. При этом преобразование, осуществляемое аналитической функцией, сохраняет эти углы во всех точках, где производная отображающей функции отличается от нуля. Теперь вопрос может быть сформулирован таким образом: какие же практические преимущества можно получить, используя метод конформных отображений?
Остановимся лишь