И ПЕРЕЧИСЛИМЫЕ ЯЗЫКИ
Контекстно-свободные грамматики недостаточно «сильны» в смысле порождающей способности, чтобы учесть все синтаксические правила языка программирования (так, все встречающиеся переменные должны быть объявлены) или чтобы вычислить относительно простые функции (например, { 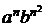 | n ³ 0}). Поэтому как обобщение контекстно-свободных грамматик введем грамматику Ван-Вайнгаардена.
| n ³ 0}). Поэтому как обобщение контекстно-свободных грамматик введем грамматику Ван-Вайнгаардена.
Грамматика Ван - Вайнгаардена есть шестерка G = (VZ, VM, S, R, P, S), причем
(i) VZ – алфавит, называемый алфавитом синтаксических знаков, который не содержит <, >;
(ii) VM – конечное множество (которое может быть и пустым), называемое множеством метапонятий, где VM Ç (VZ È {<, >}) = Æ и V = VM È VZ;
(iii) S - алфавит, называемый алфавитом базовых или терминальных символов, такой что VM Ç S = Æ;
(iv) R Ì VM ´ V * - конечное множество метапродукций;
(v) P Ì < V *> ´ (< V *> È S)* - конечное множество схем продукций;
(vi) S Î < 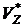 > - стартовая переменная.
> - стартовая переменная.
Пусть G = (VZ, VM, S, R, P, S) - грамматика Ван-Вайнгаардена. Тогда назовем GA = (VM, VZ, R, A) - грамматикой, ассоциированной с метапонятием A Î VM. Грамматика GA - контекстно-свободная и порождает контекстно-свободный язык L (GA) Í 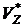 . Из схем продукций получают с помощью контекстно-свободного языка L (GA), A Î VM, продукции, которые потом применимы в выводах. Чтобы из некоторой схемы продукции получить продукцию, следует все встречающиеся метапонятия согласованно заменить словами из языка L (GA). Это значит, что если некоторое метапонятие A встречается многократно, то все встречаемые A должны быть заменены одним и тем же словом из L (GA).
. Из схем продукций получают с помощью контекстно-свободного языка L (GA), A Î VM, продукции, которые потом применимы в выводах. Чтобы из некоторой схемы продукции получить продукцию, следует все встречающиеся метапонятия согласованно заменить словами из языка L (GA). Это значит, что если некоторое метапонятие A встречается многократно, то все встречаемые A должны быть заменены одним и тем же словом из L (GA).
Как ранее, будем писать для (<a>, b1), …,(<a>, b n) Î P также <a>::= b1 | … | b n и для (A, a1), …,(A, a n) Î R также A::= a1 | … | a n.
Гомоморфизм h: (V È S È {<, >})* ® (VZ È S È {<, >})* называется допустимым (в отношении грамматики G) тогда и только тогда, когда h (a) = a, a Î VZ È S È {<, >}, h (А) Î L (GA), A Î VM.
Множество продукций 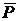 определяется следующим образом:
определяется следующим образом:
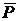 = {< h (a)> ® h (b) | <a>::= b Î P, aÎ V *, b Î (< V *> È S)*,
= {< h (a)> ® h (b) | <a>::= b Î P, aÎ V *, b Î (< V *> È S)*,
h – допустимый гомоморфизм}.
(Для различения метапродукций от схем продукций будем записывать продукции в виде: < 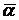 > ®
> ® 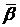 .)
.)
С помощью множеств продукций 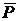 определяется прямое отношение вывода ÞG (или просто Þ) над (<
определяется прямое отношение вывода ÞG (или просто Þ) над (< 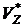 > È S)*:
> È S)*:
j ÞG y Û j = g< 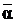 >d, y = g
>d, y = g  d, <
d, < 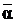 > ®
> ®  Î
Î 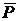 , g, d Î (<
, g, d Î (< 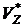 > È S)*.
> È S)*.
С помощью L (G) снова обозначим язык, порожденный грамматикой G:
L (G) = { w Î S* | S Þ* w }.
При этом Þ* есть рефлексивное и транзитивное замыкание отношения Þ и называется отношением вывода.
Формальный язык L Í S* называется перечислимым, если существует грамматика Ван-Вайнгаардена, такая что L = L (G).
Предложение 2.1. Любой контекстно-свободный язык перечислим.
Доказательство. Пусть < wi >::= b i 1 | … | 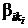 , 1 £ i £ n, – продукции контекстно-свободной грамматики G, записанные в нормальной форме Бэкуса, < w 1> - начальная переменная G, VZ - алфавит с wi Î
, 1 £ i £ n, – продукции контекстно-свободной грамматики G, записанные в нормальной форме Бэкуса, < w 1> - начальная переменная G, VZ - алфавит с wi Î 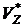 , 1 £ i £ n и S - терминальный алфавит. Тогда грамматика Ван-Вайнгаардена G = (VZ, Æ, S, Æ, P, < w 1>), причем P точно содержит продукции в нормальной форме Бэкуса в G, порождает тот же самый язык. □
, 1 £ i £ n и S - терминальный алфавит. Тогда грамматика Ван-Вайнгаардена G = (VZ, Æ, S, Æ, P, < w 1>), причем P точно содержит продукции в нормальной форме Бэкуса в G, порождает тот же самый язык. □
Чтобы избежать повторов в примерах, условимся о следующем.
Пусть G = (VZ, VM, S, R, P, S) - грамматика Ван-Вайнгаардена. Все встречающиеся большие буквы есть метапонятия в VM, все встречающиеся маленькие буквы и специальные знаки есть синтаксические знаки в VZ или терминальные символы в S, S обозначается как <начало>. Тем самым должны быть только заданы множества R и P. Теперь с помощью примеров покажем, как определенные синтаксические конструкции языков (языков программирования) могут быть представлены с помощью грамматики Ван-Вайнгаардена, соответственно как с помощью этой грамматики могут быть вычислены функции. Контекстно-свободные грамматики для этого слишком слабы.
Пример 2.1. Пусть L = { 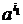 b …
b … 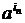 b
b 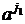 d …
d … 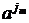 d | ik ¹ il, ik ³ 1 для 1 £ k, l £ n, k ¹ l, js Î { ik | 1 £ k £ n }, 1 £ s £ m, m, n ³ 1}. Слова ai могут пониматься как обозначения переменных в блоке объявления переменных, слова b - как разделительные знаки и d - как правые части присваиваний. Таким образом, L содержит в точности те «куски» программы, в которых все объявленные переменные различно обозначены и в которых объявлены все переменные, встречающиеся в левой части присваивания.
d | ik ¹ il, ik ³ 1 для 1 £ k, l £ n, k ¹ l, js Î { ik | 1 £ k £ n }, 1 £ s £ m, m, n ³ 1}. Слова ai могут пониматься как обозначения переменных в блоке объявления переменных, слова b - как разделительные знаки и d - как правые части присваиваний. Таким образом, L содержит в точности те «куски» программы, в которых все объявленные переменные различно обозначены и в которых объявлены все переменные, встречающиеся в левой части присваивания.
Метапродукции в R заданы посредством:
K::= aK | a, K 1::= K | e, K 2::= K | e,
L::= KbL | Kb, L 1::= L | e, L 2::= L | e.
Схемы продукций в P заданы посредством:
< начало >::= < L > < проверить L > < применить L >,
< KbL >::= < K > b < L >, < Kb >::= < K > b, < aK >::= a < K >,
< a >::= a,
< проверить KbL >::= < K не лежит в L > < проверить L >,
< проверить Kb >::= e,
< K 1 не лежит в K 2 bL >::= < K 1 не равно K 2> < K 1 не лежит в L >,
< K 1 не лежит в K 2 b >::= < K 1 не равно K 2>,
< K 1 K не равно K 1>::= e,
< K 1 не равно K 1 K >::= e,
< применить L 1 KbL 2>::= < K > d < применить L 1 KbL 2> | < K > d.
Получим:
L (Gk) = { ai | i ³ 1}, L (GL) = { 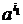 b …
b … 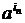 b | ik ³ 1, 1 £ k £ n, n ³ 1}.
b | ik ³ 1, 1 £ k £ n, n ³ 1}.
Зададим некоторые продукции в 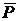 :
:
< начало > ® < a 2 bab > < проверить a 2 bab > < применить a 2 bab > поэтому L Þ* a 2 bab (в GL);
< проверить a 2 bab > ® < a 2 не лежит в ab > < проверить ab >, поэтому K Þ* a 2, L Þ* ab (в GK, GL);
< a 2 не лежит в ab > ® < a 2 не равно a >, поэтому K 1Þ* a 2, K 2Þ* a;
< a 2 не равно a > ® e, поэтому K 1 Þ* a, K Þ* a;
< применить a 2 bab > ® < a 2> d < применить a 2 bab >, поэтому L 1 Þ* e, K Þ* a 2, L 2 Þ* ab;
< применить a 2 bab > ® < a 2> d, поэтому L 1 Þ* e, K Þ* a 2, L 2 Þ* ab.
Слово a 2 baba 2 dada 2 d выводится следующим образом (в G):
< начало > Þ < aabab > < проверить aabab > < применить aabab >
Þ* aabab < проверить aabab > < применить aabab > aаbab < aa не лежит в ab > < проверить ab > < применить aabab >
Þ* aabab < проверить ab > < применить aabab > Þ aabab < применить aabab >
Þ* aababaad < применить aabab > Þ aababaad < a > d < применить aabab >
Þ aababaadad < применить aabab > Þ* aababaadadaad. □
Каждому выводу в грамматике Ван-Вайнгаардена G = (VZ, VM, S, R, P, S) можно сопоставить направленное дерево, узлы которого маркированы с помощью элементов из множества < 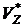 > È S.
> È S.
1. Выводу S Þ A 1… An, Ai Î < 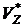 > È S соответствует дерево вывода (1) на странице 7.
> È S соответствует дерево вывода (1) на странице 7.
2. Пусть выводу S Þ* a1 A a2, a1, a2 Î (< 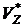 > È S)*, A Î <
> È S)*, A Î < 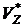 > соответствует первое дерево вывода (2) на странице 7. Тогда выводу S Þ* a1 A a2 Þ a1 A 1 … An a2, Ai Î <
> соответствует первое дерево вывода (2) на странице 7. Тогда выводу S Þ* a1 A a2 Þ a1 A 1 … An a2, Ai Î < 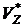 > È S соответствует второе дерево вывода (2) на странице 8.
> È S соответствует второе дерево вывода (2) на странице 8.
Как и ранее, получают результат дерева вывода.
Пример 2.2. Выводу в примере 2.1 соответствует дерево вывода:

Пример 2.3. Функция Аккерманна f: ¥ ´ ¥ ® ¥ определяется следующим образом:
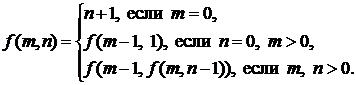
Справедливо следующее:
f (1, 1) = f (0, f (1, 0)) = f (0, f (0, 1)) = f (0, 2) = 3.
Мы хотим «вычислить» функцию Аккерманна посредством некоторой грамматики Ван-Вайнгаардена G, то есть должно выполняться:
L (G) = {1 m  1 n
1 n  1 f ( m , n ) | n, m ³ 0}.
1 f ( m , n ) | n, m ³ 0}.
(Число n представляется в виде 1 n .)
Метапродукции в R заданы посредством:
M::= M 1 | e, N::= M, S::= Sf (N, | e, T::=) T | e.
Схемы продукции в P заданы посредством:
< начало >::= < M >*< N >*< f (M, N)>,
< Sf (, N) T >::= < SN 1 T >, < Sf (M 1,) T >::= < Sf (M, 1) T >,
< Sf (M 1, N 1) T >::= < Sf (M, f (M 1, N)) T >,
< N 1>::= < N >1, <e>::= e.
Слово 1*1*111 выводится следующим образом:
< начало > Þ <1>*<1>*< f (1, 1)> Þ* 1*1*< f (1, 1)>
Þ 1*1*< f (, f (1,))> Þ 1*1*< f (, f (, 1))>
Þ 1*1*< f (, 11)> Þ 1*1*<111> Þ* 1*1*111. □
Введем теперь грамматики, которые будут рассматриваться как обобщение контекстно-свободных грамматик. Грамматика G задана посредством G = (Ф, S, P, S), причем:
(i) Ф – алфавит, называемый алфавитом переменных (англ. nonterminals).
(ii) S– алфавит, называемый алфавитом терминальных символов (англ. terminals), причем Ф Ç S = Æ (пустое множество). Посредством V = Ф È S обозначается совокупный алфавит.
(iii) Р – конечное множество продукций или правил замещения (англ. productions) вида a ® b, причем a Î V + и b Î V *. Таким образом, Р есть конечное отношение над V *.
(iv) S Î Ф переменная, называемая стартовой переменной (англ. start symbol).
Для отличия от остальных грамматик грамматику G называют также грамматикой Хомского типа 0.
Теперь мы хотим определить, какой формальный язык порождает грамматика. Для этого нам понадобится определение отношения вывода Þ, которое вводится через отношение ®.
Þ G есть отношение над V *, определяемое следующим образом:
j Þ G y тогда и только тогда, когда j = gad, y = gbd и a ® b Î P.
Как и раньше, говорят: j непосредственно выводит y или: y может быть непосредственно выведено из j.
Отношение Þ 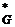 есть снова рефлексивная и транзитивная оболочка отношения Þ G. Говорят также: j выводит y, или y может быть выведено из j. В случае, если ясно какая грамматика имеется в виду, вместо Þ G и Þ
есть снова рефлексивная и транзитивная оболочка отношения Þ G. Говорят также: j выводит y, или y может быть выведено из j. В случае, если ясно какая грамматика имеется в виду, вместо Þ G и Þ 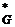 можно также писать Þ и Þ*.
можно также писать Þ и Þ*.
Слово a Î V * называется сентенциальной формой, если S Þ* a. Обозначим через L (G) формальный язык, который порождается грамматикой G. L (G) есть множество слов
L (G) = { w | w Î S* и S Þ* w }.
Это означает то, что L (G) содержит в точности все те сентенциальные формы, которые являются словами над терминальным алфавитом.
Путем введения ограничений на разрешаемые продукции получают так называемую иерархию грамматик по Хомскому.
Пусть G = (Ф, S, P, S) - грамматика. Она называется контекстно-зависимой, или грамматикой Хомского типа 1 тогда и только тогда, когда каждая продукция a ® b Î P:
(i) имеет вид a = a1 A a2, в случае b = a1ga2, A Î Ф, a1a2 Î V *, g Î V +;
(ii) имеет вид S ® e, в случае если S не встречается в правой части продукции.
Контекстно-свободные и регулярные грамматики, получаемые из грамматик типа 0 введением ограничений, называются в этой связи грамматиками типа 2 и типа 3.
Грамматика G называется ограниченной тогда и только тогда, когда для каждого правила продукции a ® b Î P выполняется: |a| £ |b|, или, если S не встречается в правой части продукции, когда выполняется a = S и b = e.
Можно легко показать, что справедливо следующее предложение.
Предложение 2.2. Формальный язык может порождаться контекстно-зависимой грамматикой тогда и только тогда, когда он может порождаться ограниченной грамматикой. □
Формальный язык называется контекстно-зависимым, если найдется контекстно-зависимая грамматика, которая порождает этот язык.
Пример 2.4. Ограниченная грамматика G = ({ S, A, B }, { a, b }, P, S), где
P = {S ® abc, S ® aAbc, Ab ® bA, Ac ® Bbcc, bB ® Bb, aB ® aaA, aB ® aa}
порождает язык L (G) = { anbncn | n ³ 1}. (Для доказательства следует рассмотреть сентенциальные формы aiAbici i ³ 1и выводимые из них формы.) Этот язык является также контекстно-зависимым. Можно показать, что L (G) не является контекстно-свободным. □
Справедливо следующее предложение.
Предложение 2.3. Формальный язык порождается грамматикой Ван-Вайнгаардена тогда и только тогда, когда он порождается грамматикой Хомского типа 0. □
Теперь мы хотим определить автоматы, которые принимают перечислимые языки. По историческим причинам эти автоматы называются машинами Тьюринга. Машину Тьюринга можно рассматривать как прибор, который имеет конечное число состояний и в обе стороны потенциально бесконечную ленту с головкой чтения-записи. Лента разделена на ячейки, в каждой ячейке находится один символ ленты. Почти все ячейки содержат специальный символ ленты, символ пробела е. Головка чтения-записи может читать и изменять содержимое ячейки. Машина Тьюринга стартует в заданном начальном состоянии, причем головка чтения-записи находится над первым (крайним слева) символом входного слова. Один такт машины Тьюринга (в зависимости от состояния и читаемого символа) состоит из следующих действий:
1) прочитанный символ стирается и на его месте записывается новый символ;
2) головка чтения-записи перемещается на одну ячейку влево или вправо;
3) машина Тьюринга переходит в новое состояние.
Машина Тьюринга может применяться для представления некоторой (в общем случае частичной) функции или для акцептирования некоторого формального языка следующим образом:
(i) Машина Тьюринга заканчивает свои вычисления с входным словом w. Содержимое ленты по окончании вычисления означает тогда значение функции от аргумента w, в случае, если представляется функция. Если должен акцептироваться язык, то слово w тогда и только тогда содержится в языке, когда машина Тьюринга находится по окончании вычисления в конечном состоянии.
(ii) Процесс вычислений на машине Тьюринга не прерывается. Тогда функция для аргумента w не определена. Соответственно, слово w не содержится в языке.
Двусторонняя детерминированная машина Тьюринга T = (Q, S, Г, d, q 0, F) определяется через:
(i) конечное множество состояний Q;
(ii) входной алфавит S;
(iii) алфавит символов ленты Г. При этом Г содержит символ пробела е и выполняется: S Í Г - { e };
(iv) функция перехода в общем случае лишь частично определенная:
d: (Q - F) ´ Г ® Q ´ Г ´ {L, R};
(v) начальное состояние q 0 Î Q;
(vi) множество конечных состояний F Í Q.
Вычисление на машине Тьюринга представляется через конфигурации, причем конфигурация (или ситуация) есть элемент из Г* Q Г*. (При этом Q, Q Ç Г = Æ используется как алфавит). Конфигурация a q b интуитивно означает, что машина Тьюринга находится в состоянии q, что ab есть содержимое ленты и что головка чтения-записи читает первый символ слова b.
Условимся, что конфигурация a q b означает то же самое, что и конфигурация en a q b em, n, m ³ 0.
Один шаг вычислений машины Тьюринга T представляется отношением над конфигурациями. Это отношение определяется следующим образом через d:
(i) a qA b a Bp b, если d(q, A) = (p, B, R),
(ii) a CqA b a pCB b, если d(q, A) = (p, B, L),
A, B, C Î G, a, b Î G*, q Î Q - F, p Î Q.
(На основе нашего соглашения выполняется:
q peB, если d(q, e) = (p, B, L), a q a Bp, если d(q, e) = (p, B, R).)
Говорят также, что отношение прямо переводит одну конфигурацию в другую. Отношение 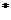 переводит некоторую конфигурацию в другую.
переводит некоторую конфигурацию в другую.
Конечная конфигурация есть конфигурация a qA b, такая, что d(q, A) не определена. (В случае, если q Î F, то a qA b автоматически конечная конфигурация.)
Машина Тьюринга Т останавливается при вводе слова (w 1, …, wn), wi Î S*, 1 £ i £ n в конечной конфигурации a q b, когда
q 0 w 1 ew 2 e … ewn 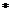 a q b.
a q b.
Пусть h: G* ® (G - { e })* - гомоморфизм, который определен через h (A) = A, A Î G - { e }, h (e) = e. Пусть T - некоторая машина Тьюринга и n ³ 0. n - местная частичная функция fT,n: (S*) n ® G*, которая представляется (или вычисляется) машиной T, задается как:

n -местная частичная функция f: (S*) n ® G* называется частично вычислимой по Тьюрингу, если существует такая машина Тьюринга, что
fT,n (w 1, …, wn) = f (w 1, …, wn),
для всех (w 1, …, wn) Î (S*) n.
Частично вычислимая по Тьюрингу функция называется полностью вычислимой по Тьюрингу, если T останавливается для всех входных слов (w 1, …, wn) Î (S*) n.
Формальный язык L Í S*, принимаемый машиной Тьюринга T, определяется через:
L = { w | q 0 w 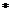 a q b, w Î S*, q Î F, a, b Î G*}.
a q b, w Î S*, q Î F, a, b Î G*}.
Формальный язык над S называется перечислимым по Тьюрингу, если он принимается некоторой машиной Тьюринга. Он называется разрешимым по Тьюрингу, если он принимается некоторой машиной Тьюринга, которая останавливается для всех входных слов w Î S*.
Пример 2.6. Мы хотим построить машину Тьюринга T, которая принимает формальный язык { anbncn | n ³ 1}:
T = (Q, S, Г, d, q 0, F), где
Q = (q 0, q 1, q 2, q 3, q 4, q 5, q 6, q 7, qf), S = { a, b, c }, G = (a, b, c, X, e }, F = { qf };
Функция перехода d определена следующим образом:
| d(q 0, a) = (q 1, a, R) d(q 1, a) = (q 1, a, R) d(q 1, b) = (q 2, b, R) d(q 2, b) = (q 2, b, R) d(q 2, c) = (q 3, c, R) d(q 3, c) = (q 3, c, R) d(q 3, e) = (q 4, e, L) | Проверка, выполнено ли w Î a + b + c +. Если да, то T переходит в состояние q 4. В противном случае T останавливается в одном из состояний q 0, q 1, q 2 или q 3, не акцептируя слово. |
| d(q 4, X) = (q 4, X, L) d(q 4, c) = (q 5, X, L) | Головка передвигается налево до символа c. Он заменяется на X. |
| d(q 4, e) = (qf, e, R) | При пробеге влево в состоянии q 4 на ленте находятся только символы X. T акцептирует слово. |
| d(q 5, c) = (q 5, c, L) d(q 5, X) = (q 5, X, L) d(q 5, b) = (q 6, X, L) | Головка передвигается дальше налево до символа b, который заменяется на X. |
| d(q 6, b) = (q 6, b, L) d(q 6, X) = (q 6, X, L) d(q 6, a) = (q 7, X, R) | Головка передвигается дальше до символа a, который заменяется на X. |
| d(q 7, X) = (q 7, X, R) d(q 7, b) = (q 7, b, R) d(q 7, c) = (q 7, c, R) d(q 7, e) = (q 4, e, L) | Головка возвращается на самый крайний справа символ X, и T снова попадает в состояние q 4. |
Если в состоянии q 4 будет найден один из символов a или b, то T останавливается, не акцептируя слово. Потому что тогда число символов a или b во входном слове больше, чем число символов c. Если в состоянии q 5 или q 6 не будет найдено b или a, то аналогично T останавливается, не акцептируя слово, так как тогда число символов c во входном слове больше, чем количество b или a.
Слово w = a 3 b 3 c 3 принимается следующим образом:
q 0 aaabbbccc * aaabbbсссq 3 aaabbbccq 4 c
aaabbbcq 5 cX * aaabbq 5 bccX aaabq6bXccX *
* aaq 6 abbXccX aaXq 7 bbXccX * aaXbbXccq 4 X
aaXbbXcq 4 cX aaXbbXq 5 cXX * aaXbq 5 bХcXX
aaXq 6 bXXcXX * aq 6 aXbXXcXX aXq 7 XbXXcXX *
* aXXbXXcXq 4 X * aXXbXXq 4 cXX aXXbXq 5 XXXX *
* aXXq 5 bXXXXX aXq 6 XXXXXXX * q 6 aXXXXXXXX
* Xq 7 XXXXXXXX * XXXXXXXXq 4 X * q 4 eXXXXXXXXX
qfXXXXXXXXX.
Акцептирование anbncn требует O (n 2) шагов. □
Пример 2.7. Построим теперь машину Тьюринга, которая при вводе an, n ³ 0 вычисляет двоичное представление числа n как слово над {0, 1}:
T = (Q, S, Г, d, q 0, F),
где Q = (q 0, q 1, q 2, q 3), S = { a }, G = (a, 0, 1, e }, F = Æ;
Функция перехода d определена следующим образом:
| d(q 0, e) = (q 2, 0, L) | При вводе e = а 0 возвращается 0. |
| d(q 0, a) = (q 1, a, R) d(q 1, a) = (q 1, a, R) d(q 1, 0) = (q 1, 0, R) d(q 1, 1) = (q 1, 1, R) d(q 1, e) = (q 2, e, L) | Головка передвигается на крайний справа, отличный от е символ. Если этот символ 0 или 1, то вычисление закончено. |
| d(q 2, a) = (q 3, e, L) d(q 3, a) = (q 3, a, L) | Если это символ а, то он замещается на е, и головка передвигается влево до двоичного числа, стоящего перед группой символов а. |
| d(q 3, 0) = (q 1, 1, R) d(q 3, 1) = (q 3, 0, L) d(q 3, e) = (q 1, 1, R) | К этому двоичному числу добавляется 1. |
Двоичное представление числа 6 вычисляется следующим образом:
q 0 aaaaaa * aaaaaq 2 a aaaaq 3 a * q 3 eaaaaa
1 q 1 aaaaa * 1 aaaaq2a 1 aaaq 3 a * q 31 aaaa
q 3 e 0 aaaa 1 q 10 aaaa * 1 q 30 aaa 11 q 1 aaa *
* 1 q 31 aa q 310 aa q 3 e 00 aa 1 q 100 aa *
* 10 q 30 a 101 q 1 a * 10 q 31 1 q 300
11 q 10 110 q 1 11 q 20.
Вычисление двоичного представления числа n требует O(n 2) шагов. Существует «более сложная» машина Тьюринга, которая вычисляет двоичное представление за O(n log n) шагов. □
Как модификацию двусторонней детерминированной машины Тьюринга рассмотрим одностороннюю детерминированную машину Тьюринга. Она имеет ленту, которая потенциально бесконечна только в одну сторону. Конец ленты маркируется некоторым специальным символом, например Z0, который не должен меняться.
Пусть Т 2 двусторонняя машина Тьюринга. Тогда односторонняя машина Тьюринга Т 1 моделирует двустороннюю машину Тьюринга Т 2 следующим образом. Начальный участок ленты машины Т 1 при необходимости разделяется на две дорожки (т. е. алфавит ленты машины Т 1 содержит Г ´ Г, где Г – алфавит ленты Т 2). Вторая дорожка служит для того, чтобы представлять содержание ячеек машины Т 2, которые лежат левее той ячейки, над которой находится головка чтения-записи в начале вычислений. В своем множестве состояний Т 1 «отмечает», находится она на верхней или на нижней дорожке (т. е. множество состояний машины Т 1 содержит Q ´ {вверху, внизу}, где Q – множество состояний машины Т 2). Если, например, машина Т 2, исходя из начальной конфигурации, q 0 a 1 a 2 a 3 a 4 a 5 делает три шага влево, при которых последовательно записываются символы А 1, А 2, А 3, то достигаемая тем самым конфигурация qeA 3 A 2 A 1 a 2 a 3 a 4 a 5 машины Т 2 представляется с помощью машины Т 1 следующим образом:
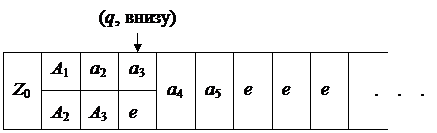 |
Если машина Т 2 выполняет передвижение вправо, то и машина Т 1, если она находится в состоянии (q, вверху), тоже выполняет движение вправо. Если же машина Т 1, как в предыдущем примере, находится в состоянии (q, внизу), то она выполняет движение влево. Подобное справедливо при передвижении машины Т 2 влево. Если Т 1 достигает символа Z 0, то она должна перейти из состояния (q, внизу) в (q, вверху), или наоборот.
В конце вычислений, если должна представляться функция, все символы должны быть сдвинуты на верхнюю дорожку и пары 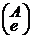 заменяются на А.
заменяются на А.
В следующем предложении мы сформулируем, что языки, принимаемые машинами Тьюринга, есть в точности перечислимые языки.
Предложение 2.4. Пусть L - формальный язык. Тогда следующие высказывания эквивалентны:
(i) Существует грамматика Ван-Вайнгаардена, которая порождает L.
(ii) Существует грамматика Хомского типа 0, которая порождает L.
(iii) Существует двусторонняя детерминированная машина Тьюринга, которая принимает L.
(iv) Существует односторонняя детерминированная машина Тьюринга, которая принимает L.
Доказательство. Мы покажем только моделирование действий односторонней машины Тьюринга T = (Q, S, Г, d, q 0, F) грамматикой типа 0 G = ({ S, T, $} È Q È (G - S), S, P, S). При этом следующие продукции лежат в Р:
(i) S ® TZ 0 q 0, T ® $, T ® aTa, a Î S.
Эти продукции осуществляют вывод S Þ* w $ w R Z 0 q 0, где w Î S*.
(ii) aq ® pb для d(q, a) = (p, b, R),
aqc ® bcp для d(q, a) = (p, b, L),
$ ® $ e.
Применяя эти продукции, мы можем моделировать действия машины Тьюринга Т: S Þ* w $ 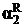 q
q 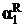 тогда и только тогда, когда q 0 Z 0 w *a1 q a2.
тогда и только тогда, когда q 0 Z 0 w *a1 q a2.
(iii) qz ® q, zq ® q, $ q ® e, q Î F, z Î G.
Если Т достигает конечной конфигурации a1 q a2, q Î F, то с помощью продукций (i), (ii) возможен вывод: S Þ* w $ 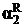 q
q 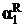 . С помощью продукций (iii) возможен следующий вывод: w $
. С помощью продукций (iii) возможен следующий вывод: w $ 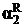 q
q 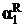 Þ* w. □
Þ* w. □
Рассмотрим другую модификацию машины Тьюринга – многоленточную машину. Детерминированная k-ленточная машина Тьюринга имеет k лент, потенциально бесконечных в обе стороны. Над каждой лентой находится головка чтения-записи. Функция перехода d имеет в качестве аргументов соответствующее состояние и символы, читаемые на каждой из лент. Ее значения задают новое состояние, новые символы, которые записываются на месте старых, и независимые друг от друга перемещения головок чтения-записи, которые на каждом шаге передвигаются влево (L), вправо (R) или не передвигаются (S):
d(q, A 1, …, Ak) = (p, B 1, …, Bk, S 1, …, Sk),
где q, p Î Q, Ai, Bi Î G, Si Î {L, S, R}.
(Также и в рассматривающихся до сих пор моделях машин Тьюринга возможно допустить отсутствие передвижения головки чтения-записи при прямом переходе. Тем самым вычислительная «сила» машины Тьюринга не повышается – только что «программирование» становится удобней.)
Конфигурация k -ленточной машины Тьюринга есть элементы из (Q ´ (G*¸G*) k. При этом специальный символ ¸ обозначает положение головки чтения-записи на соответствующей ленте. Таким образом, конфигурации имеют вид:
(q, a1¸b1, a2¸b2, …, a k ¸b k).
Входное слово (w 1, …, wn) представляется конфигурацией (q 0, ¸ w 1 e … ewn, ¸, …, ¸). Переход от одной конфигурации к другой осуществляется детерминированным образом с помощью функций перехода. Остальные определения, которые относятся к машинам Тьюринга, переносятся аналогично.
Предложение 2.5. k -ленточная машина Тьюринга (k ³ 1) может быть смоделирована двухсторонней машиной Тьюринга.
Доказательство. Пусть Т – k -ленточная машина Тьюринга. Тогда конфигурация машины Т может быть смоделирована двухсторонней машиной Тьюринга Т 1, лента которой разделена на 2 k дорожек:
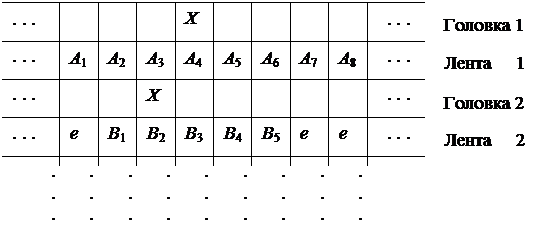 |
Дорожка «лента i » содержит содержимое i -той ленты машины Т 1, дорожка «головка i » маркирует позицию i -той дорожки, в которой находится головка чтения-записи машины Т. В состояниях машины Т 1 хранится информация о том, находится символ Х на дорожке «головка i » слева или справа от головки чтения-записи машины Т 1. Кроме того, соответствующие состояния машины Т хранятся в машине Т 1. Для моделирования перехода машины Т машина Т 1 должна найти символ Х на дорожке «головка i » и лежащий под ним символ на дорожке «лента i » занести как информацию в состояние. После просмотра всех k дорожек машина Т 1 знает, как нужно изменить k символов и как нужно выверить позиции символа Х. Тогда необходимо снова найти символ Х на дорожке «головка i », лежащий под ним символ заменить согласно функции перехода машины Т и сдвинуть при необходимости символ Х. После того как это проделано для всех дорожек, Т 1 находится в конфигурации, которая представляет последовательность конфигураций машины Т. Разумеется, на каждом шаге нужно следить за тем, чтобы информация о том, находится символ Х на дорожке «головка i » слева или справа от головки чтения-записи машины Т 1, была занесена в новое состояние. □
Преимущество многоленточных машин Тьюринга состоит в том, что они в общем случае быстрее, чем одноленточные.
Пример 2.8. Мы хотим построить двухленточную машину Тьюринга, которая принимает формальный язык { anbncn | n ³ 1}:
T = (Q, S, Г, d, q 0, F),
где Q = (q 0, q 1, q 2, qf), S = { a, b, c }, G = (a, b, c, e }, F = { qf }.
Функция перехода d определена следующим образом:
| d(q 0, a, e) = (q 0, a, a, R, R) | Ведущая а -группа входного слова копируется на вто
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2018-01-08 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |