Мы начнем с интуитивно ясного понятия алгоритма.
Алгоритм есть метод решения некоторой задачи с входными данными. Этот метод может быть разложен на отдельные единичные шаги, исполнение которых и порядок их следования однозначно определены. Этот метод должен иметь возможность описания с помощью текста конечной длины. При этом «решение проблемы с одним входом» есть, в сущности, вычисление значения функции для заданного аргумента.
Для того чтобы математически овладеть понятием алгоритма, следует заменить его формализованным понятием, а именно его экспликатом, т.е. интерпретацией. Существуют различные интерпретации понятия алгоритма, такие, как μ-рекурсивные функции, машины Тьюринга, грамматики типа 0, грамматики Ван-Вайнгаардена и др. При этом эти интерпретации служат также для описания алгоритмов, что означает: каждая конкретная μ-рекурсивная функция, каждая конкретная машина Тьюринга, каждая конкретная грамматика типа 0, каждая конкретная грамматика Ван-Вайнгаардена описывает определенный алгоритм; она, таким образом, репрезентирует алгоритм. Мы в дальнейшем не будем делать строгого различия между конкретным алгоритмом и его возможными описаниями (если это не приведет к неясности). Все эти интерпретации эквивалентны в том смысле, что каждый алгоритм, который может быть описан с помощью одной из этих интерпретаций, таким же образом может быть описан и с помощью любой другой из этих интерпретаций. Также и любой формально определенный язык программирования с определенными минимальными требованиями (как, например, присваивание и структура циклов) может рассматриваться как интерпретация понятия алгоритма. В это число попадают все имеющиеся языки программирования (машинный код, Ассемблер, Бейсик, Алгол 60, Алгол 68, Фортран, Паскаль, Модула-2, Лисп, …).
Мы рассмотрим сначала такие алгоритмы, отдельные шаги которых состоят в изменении слов над заданным алфавитом. Если достигается конец этого процесса изменения, то полученное слово есть результат алгоритма при некотором определенном входе. Если же при некотором определенном входе конец этого процесса изменения не достигается, то результат не определен.
Мы будем полагать теперь, что понятие алгоритма формально определено, а именно с помощью однойиз приведенных интерпретаций. (Для дальнейшего достаточно выбрать некоторый язык программирования и описать алгоритмы с помощью программ на этом языке.) Мы хотим далее с помощью понятия алгоритма получить другие понятия и рассмотреть основы теории рекурсивных функций.
Пусть М – бесконечное множество, тогда М является эффективно нумерованным (счетным) с помощью биективной функции F: М ®¥ тогда и только тогда, когда для всех входных данных из ¥найдется алгоритм, с помощью которого для любого п Î¥ может быть эффективно вычислено значение обратной к F функции в точке п, т.е. F -1(п) Î М. В случае, если М конечно, где ç М ç =п, то в этом определении ¥ следует заменить на {0,1,..., п -1}.
Таким образом, можно говорить об n -м элементе F -1(п) множества М. Если обозначить F -1(п)через xn, то последовательность
x 0, х 1,…, хn,…
является эффективной нумерацией множества М. Элемент х Î М имеет тогда индекс F (х)Î ¥. Также говорят, что F кодирует М, F -1 декодирует М.
Пример 3.1. (1) Пусть S={a1,...,a k } – алфавит. Лексикографический порядок над å*определяется следующим образом:
Пусть w 1, w 2 Îå*. Тогда w 1 £ w 2 Û
(i) | w 1| £ | w 2|, или
(ii) | w 1| = | w 2|, w 1 = v a i v 1, w 2 = v a j v 2, i < j, v, v 1, v 2 Î å*, или
(iii) w 1 = w 2
Порядок £ является полным и нётеровым и å* может быть эффективно занумеровано согласно лексикографическому порядку. Иногда также следующий порядок называется лексикографическим:
w 1 £ ’ w 2 Û
(i) w 2 = w 1 v, v Îå*, или
(ii) w 1 = v a i v 1, w 2 = v a j v 2, i < j, v, v 1, v 2 Î å*.
Этот порядок£ ’ полный, но не нётеров:
a2 > ’ а1а2> ’ a1a1a2 > ’ …> ’ a 
a2> ’ …
В лексике применяется этот лексикографический порядок.
(2) Пусть М =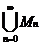 
, Мп – конечно, причем |Мn|=kn, kn >0, Мi 
Мj= Æ для i ¹ j. Пусть Мn эффективно нумеровано посредством функции Fn: Мп ® {0,1,…, kn -1}, тогда последовательность
F 
(0),..., F (k 0 – 1), F 
(0),..., F (k 1 – 1),..., F 
(0),..., F (kn – 1),...
является эффективной нумерацией множества М.
(3) Множество D 1× D 2, где D 1 и D 2являются эффективно счетными, само является эффективно счетным. Пусть Di эффективно нумеруется посредством Gi: Di ®¥, i= 1,2.
Определим для п ³ 0,
Мn = {(d 1, d 2)| G 1 (d 1)+ G 2(d 2) = n, d 1Î D 1, d 2Î D 2 }
и
Fn ((d 1, d 2)) = G 1 (d 1) = n – G 2(d 2), (d 1, d 2) Î Мn.
Тогда, согласно (2), последовательность
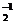(G (0), G 
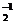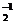(0)), (G (0), G (1)), (G (1), G (0)),(G (0), G 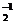(2)),…
является эффективной нумерацией D 1× D 2. Oна называется диагональной нумерацией. ÿ
В дальнейшем, пусть Е и D – эффективно счетные множества. (Большей частью Е = 
×…× 
, D = å*). Тотальная функция F: Е ® D называется вычислимой (а также рекурсивной), тогда и только тогда, когда существует один для всех аргументов из Е завершающийся алгоритм, с помощью которого для каждого аргумента x Î Е можно эффективно вычислить значение функции F (x) Î D. Частичная функция F: Е ® D называется частично вычислимой (а также частично рекурсивной) тогда и только тогда, когда существует алгоритм, который обеспечивает следующее. Если F (x), x Î Е, определено, то алгоритм завершается при вводе х и возвращает F (x) Î D); если F (x), x Î Е, не определено, то при вводе х алгоритм не завершается за конечное время.
Тем самым понятия «алгоритм» и «частично вычислимая функция» соответствуют друг другу в следующем смысле: каждый алгоритм определяет частично вычислимую функцию, которая посредством него вычисляется.
Полагая в предыдущих определениях E =¥× … ×¥ ,D= ¥, получают числовые вычислимые и соответственно частично вычислимые функции. В сущности, можно ограничиться числовыми функциями 
: ¥®¥. Именно пусть G: Е ® D вычислимая (соответственно частично вычислимая) функция. Тогда существуют биективные функции F 1: Е ®¥ и F 2 : D ®¥, такие, что Е посредством F 1и D посредством F 2 – эффективно счетные. Пусть : ¥®¥ – функция, определяемая посредством:
(n) = F 2(G (F (n))), п Î¥.
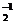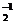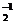Очевидно, является вычислимой (соответственно частично вычислимой) и выполняется: G (x) =F ( (F 1(x))), х Î Е. Действительно, из определения следует: F ( (n)) = G (F (n)). Положим теперь х= F (n), тогда п = F 1(x) и F ( (F 1(x))) =G (x).
Множество М Í D называется рекурсивно перечислимым тогда и только тогда, когда существует вычислимая функция F: Е ® D, с подходящим образом выбранным множеством Е, такая, что область значений функции F совпадает с М, т.е., М ={ F (x) | х Î Е } или, короче, М = F (E). В дальнейшем пустое множество Æ также является рекурсивно перечислимым.
Название «перечислимое» множество отражает следующую сущность: Пусть z 0, z 1,…, zn, …– эффективная нумерация Е. Тогда M может быть перечислено посредством
F (z 0), F (z 1), …, F (zn), …
Множество М Í D называется рекурсивно разрешимым (или рекурсивным), если М и D – М рекурсивно перечислимы.
Так как оказывается, что введенные уже перечислимые и разрешимые формальные языки являются в точности рекурсивно перечислимыми и рекурсивно разрешимыми формальными языками, то в дальнейшем мы будем, если это не приведет к неясностям, слово «рекурсивный» опускать.
Пусть М Í D. Определим тогда характеристическую функцию c M: D ®{0,1} множества М (относительно D) посредством:
c M (x) = 
.
Тогда справедливо, что M Í D разрешимо тогда и только тогда, когда c M вычислима. Это может быть показано следующим образом:
Для М = Æ или М = D, М является разрешимым (Æ перечислимо по определению и D – перечислимо посредством тождественной функции, которая, конечно, вычислима). Далее, в этих случаях выполняется, что характеристическая функция c M является вычислимой (так как она в случае М = Æ всегда принимает значение 0 и в случае М=D всегда значение 1).
Теперь рассмотрим случай М ¹Æи М ¹ D.
(i) Пусть c M – вычислимая. Пусть 
Î М и 
Î D–М произвольные, но фиксированные элементы. Мы определим две функции F 0, F 1: D ® D как
F 0(x) = 
; F 1(x)= 
Конечно, F 0 и F 1 являются вычислимыми и выполняется: F 0(D)= D – М и F 1(D)= М. Отсюда D – М и М перечислимы и М – разрешимо.
(ii) Пусть М – разрешимо. Тогда М и D – М – перечислимы. Поскольку М ¹ Æ и М ¹ D, то существуют две вычислимые функции F 0 и F 1, которые перечисляют множества D – М и М:
D – M: у 0, у 1, …, уn,…,
M: x 0, x 1,…, xn,….
Мы хотим теперь для z Î D вычислить значение c M (z). Для этого применим следующий алгоритм: для каждого i = 0, 1,2... вычислим с помощью F 0 и F 1 элементы yi и хi. А так как z должен встретиться или в последовательности (уn), или в последовательности (xп), то существует такое т, что выполнимо z = ут или z = xm. В первом случае мы положим c M (z) = 0, а во втором случае положим c M (z)=1. Тем самым характеристическая функция c M – вычислимая.
Подобное выполняется и для перечислимых множеств. Пусть М Í D. Мы определим частичную характеристическую функцию 
: D ®{1} множества М (относительно D) посредством
(x)= 
Тогда справедливо, что М Í D перечислимо тогда и только тогда, когда – частично вычислимая. Это может быть показано следующим образом:
(i) Пусть – частично вычислимая. В случае, если (x) является не определенной для всех x Î D, тогда М = Æ и поэтому является перечислимым множеством.
Пусть теперь (
)=1 для Î D. Тогда выполняется Î М. Определим функцию F: (¥ – {0})× D ® D посредством
F ((n,x)) = 
Так как (¥ – {0})× D, согласно примеру 3.1(3), является эффективно счетным, то функция F – вычислимая. А вследствие М ={ F ((n,x)) | п ³1, x Î D }, М является перечислимым.
(ii) Пусть М – перечислимое. Для М = Æфункция нигде не определена и поэтому частично вычислимая. Для М ¹Æ существует вычислимая функция F: Е ® D, которая перечисляет М:
M: x 0, x 1, …, x n, …
Мы хотим теперь для элемента z Î D вычислить значение (z). Для этого сравним последовательно z с хi, i ³ 0. Если мы найдем т ³0, для которого z = xт, то положим (z) = 1. В противном случае (z) не определена.
Из-за этих обстоятельств перечислимые множества называют также полуразрешимыми множествами. Таким образом, справедливо, что множество М Í D разрешимо тогда и только тогда, когда М и D–М полуразрешимы.
Определим теперь важный экспликат понятия частично вычислимой функции, а именно m-рекурсивные функции. Эти функции отображают (å*)n, п ³ 0(п - кратное декартово произведение множеств å*) в å*. Сначала определим три вида простых базовых функций:
(i) Для любого а Îå отображение N a: å*® å*, N a (w) = wa, w Î å*, называется функцией следования.
(ii) Для любого п ³ 0 отображение С n:(å*)n®å*, С n (w 1, w 2,..., w n)=e, wi Îå*, 1£ i £ n, называется п-местной нуль-функцией.
(iii) Для любого п ³ 1 и 1£ j £ п отображение 
:(å*)n ® å*, (w 1, w 2,..., w n)= wj, wi Îå*, 1£ i £ n называется п-местной проекцией.
Определим далее три функционала, которые позволяют получить новые функции из уже ранее определенных функций.
(i) Пусть п ³ 0, т ³ 1 и H: (å*) m ®å*, Gj: (å*) n ®å*, 1£ j £ m. Функция F: (å*) n ® å* образуется из Н путем подстановки функций G 1, G 2,…, Gm тогда и только тогда, когда для всех wi Îå*, 1£ i£ п, выполняется:
F (w 1, w 2,..., wn)= Н (G 1 (w 1,..., wn),..., Gm (w 1,..., wn)).
(ii) Пусть n ³ 1, G: (å*) n -1®å* и На: (å*) n +1® å*, a Îå. Функция F:(å*) n ®å* образуется из G и Ha, a Îå, посредством рекурсии тогда и только тогда, когда для всех wi Îå*,1£ i £ n, имеет место
F (e, w2,…,wn) = G (w2,…,wn),
F (w1a,…,wn) = Ha (F (w 1,…, wn), w 1,…, wn), a Îå.
(iii) Пусть n ³ 0 и G: (å*) n +1®å*. Функция F: (å*) n ®å*образуется из G путем минимизации относительно a Îå тогда и только тогда, когда для всех wi Îå*, 1£ i £ п выполняется:
F (w 1, … ,wn) = ma [ G (w0,w 1 ,…,wn)].
При этом m а [ G (w 0 ,w 1, …, wn)] определена следующим образом: в случае, если найдется некоторое т ³0, такое, что G (аl,w 1 ,..., wn), 0£ l £ m, определена, причем G (аl,w 1 ,..., wn)¹e, 0£ l < m и G (аm,w1,...,wn)=e, то выполняется: m а [ G (w0,w 1 ,..., wn)] = am. В противном случае m а [ G (w0,w 1 ,..., wn)] не определена.
С помощью базовых функций и функционалов определяют примитивно рекурсивные и m-рекурсивные функции. Семейство примитивно рекурсивных (соответственно m- рекурсивных) функций над å есть наименьшее семейство функций F:(å*)n®å*, n ³0, которое содержит N a, а Îå,C0, 
, n ³1, и замкнуто относительно подстановки и рекурсии (соответственно подстановки, рекурсии и минимизации).
Ясно, что m-рекурсивная функция в общем случае является частично рекурсивной, тогда как примитивно рекурсивная функция всегда вполне m‑рекурсивна.
Из приведенных выше определений получают числовые функции из ¥n в ¥, полагая, что å одноэлементный алфавит, å={ а }, и идентифицируя am с числом т. В частности, числу 0 соответствует элемент e. Семейство числовых примитивно рекурсивных функций (соответственно числовых m- рекурсивных функций) есть наименьшее семейство функций F: ¥n ®¥, n ³ 0, которое содержит N (=N a), С0, , n ³1 и замкнуто относительно подстановки и рекурсии (соответственно подстановки, рекурсии и минимизации).
Для того чтобы получить компактное описание m-рекурсивных функций над å, введем m- рекурсивные программы. Каждая m-рекурсивная программа имеет один или несколько входов в зависимости от того, на какое количество аргументов из å* она рассчитана. Каждая п- местная m‑рекурсивная программа представляет п- местную m-рекурсивную функцию (служит для вычисления этой функции). Выберем (всюду, где это возможно) следующие обозначения: m-рекурсивная функция будет обозначаться большими буквами, m-рекурсивная программа, которая ее вычисляет, будет обозначаться теми же самыми малыми жирными буквами. Пусть å={a 1,..., a k}.
(i) Программа n 
– одноместная и представляет функцию следования N , 1£ i £ k.
(ii) Программа c – нуль-местная и представляет нуль-функцию С0.
(iii) Программа u может иметь любое число входов п ³ 1 и представляет 
.
(iv) Пусть m-рекурсивные функции Н: (å*)m ®å* иG j: (å*)n, l£ j £ n, n ³ 0, m ³ 1 представляются через т- местные (соответственно, п- местные) программы h и g j. Функция F, которая образуется путем подстановки G 1,..., Gm в Н, представляется п- местной программой h (g 1,..., g m).
(v) Пусть m-рекурсивные функции G:(å*)n-1 ®å* и Н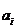 
:(å*)n+1 ®å*, 1£ i £ k, n ³ 1 представлены через (n – 1)-местные (соответственно (n +1)-местные) программы g и h 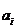. Функция F, которая образуется путем рекурсии из G и Н 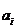, 1£ i £ k, представляется n- местной программой [ gh 
,..., h 
].
(vi) Пусть m-рекурсивная функция G: (å*)n+1®å*, n ³ 1 представлена (n +1)‑местной программой g. Функция F, которая образуется из G путем минимизации относительно a i, 1£ i £ k, представляется n- местной программой § g ¨ .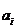
Синтаксис языка m - рекурсивных программ (без учета разрядности), таким образом, задан следующими продукциями:
P ® n |…| n | c | u | P (L)| [ Pk +1] | § P ¨ |…| § P ¨ ,
L ®PL | P
m - рекурсивная программа, в которой не встречаются символы §, ¨, называется примитивно рекурсивной программой. В случае числовых m‑рекурсивных программ k = 1 и индексы при n и § ¨опускаются:
P ® n | c | u | P (L) | [ PP ] | § P ¨.
Пример 3.2. (1) Мы хотим функции 
, п ³ 2, 2£ j £ n представить с помощью программ. Пусть u j – программа произвольной размерности большей или равной j,такая, что примененная к (w 1 ,...,wn), где n ³ j, возвращает слово wj (u 1 = u). Тогда [ u j u k ] есть программа размерности ³ j +1, такая, что примененная к (w1,..., wn), где n ³ j +1, возвращает слово wj +1. Поэтому[ u j u k ] представляет следующую функцию F:
F (e, w 2, …, wn) = 
(w2, …, wn),
F (w 1 a,w 2,…, wn) = 
(F (w 1 ,w2,…, wn), w 1 ,w 2 ,...,wn), a Îå.
Тем самым выполнено:
F (w 1 a, w 2,…, wn) =... =F (e, w 2,..., wn) = (w2,..., wn)= wj +1.
(2) Представим С n,п ³0с помощью п- местной программы c n. Функция С n представляется с помощью [ c n -1 u k ] (где c 0 = c). Тогда [ c n -1 u k ] представляет следующую функцию F:
F (e, w 2,…, wn) = C n -1(w2, …, wn),
F (w 1 a,w 2,..., wn) = (F (w 1, w2,...,wn), w 1, w2, …, wn), a Îå,
при этом выполняется:
F (w 1 a, w2,..., wn) =... = F (e, w2,..., wn) =C n- 1(w2,..., wn)=e.
(3) Представим одноместную постоянную функцию K v, v Îå*, гдеK v (w)= v, для всех w Îå*с помощью программы. Пусть k v – одноместная программа, которая представляет K v. Тогда [сuk ] представляет функциюKe = С1 и n a(k v)представляет постоянную функцию K va, a Îå. Поэтому n a (k v) представляет следующую функцию F:
F (w) =N a (K v (w)) = N a (v) = va.
Теперь мы хотим определить дальнейшие функционалы, позволяющие из примитивно рекурсивных (соответственно m-рекурсивных) функций снова получать того же рода функции.
Предложение 3.1. Пусть G:(å*) n ®å*, H:(å*) m ®å*, Ha:å*®å*, a Îå, – примитивно рекурсивные (соответственно m-рекурсивные) функции. Тогда следующие функции F тоже являются примитивно рекурсивными (соответственно m-рекурсивными):
(i) F (w 1 ,…,wn) =G (wp (1) ,…,wp(n)), где p – перестановка из {1,…, n }.
(ii) F (w 1 ,…,wl- 1 ,wl+ 1 ,…,wn,v 1 ,..,vm) =G (w 1 ,…,wl- 1 ,H (v 1 ,..,vm) ,wl+ 1 ,..,wn).
(iii) F (w 1 ,…,wn,e)= G (w 1 ,…,wn),
F (w 1 ,…,wn,w 0 a) =Ha (F (w 1 ,…,wn,w 0)) ,a Îå.
Доказательство: Функции G, H, Ha могут быть представлены программами g, h, h a, a Îå.
(i) F представяется программой g(u p(1),…, u p(n)). Поэтому справедливо:
F (w 1,…, wn)= G (U 
(w 1,…, wn),…,U 
(w 1,…, wn))= G (w p(1),…, w p(n)).
(ii) F представляется программой g (u 1… u l -1 h (u n … u n + m -1) u l … u n -1).
(iii) программа [ gh (u)… h (u)](u n +1 u 1… u n) представляет функцию F 1. Тогда справедливо:
F 1(w 1,…, wn, w 0)= F 2(w 0, w 1,…, wn),
где F2 представлятся программой [ gh (u)… h (u)], таким образом,
F2 (e, w 1 ,…,wn) = G (w 1 ,…,wn),
F2 (w0ai,w 1 ,…,wn)= 
( 
F2 (w0,w 1 ,…,wn) ,w0,w 1 ,…,wn)) =
= (F2 (w0,w 1 ,…,wn)), 1£ i £ k.
Тем самым получим
F 1(w 1, …,wn, e) = G (w 1 ,…,wn),
F 1(w 1 ,…,wn,w0a) = (F (w 1 ,…,wn,w0)), 1£ i £ k
и F 1 совпадает с F. ð
Пример 3.3. (1) Мы хотим записать программу con2 для функции CON2:å*×å*®å* с CON2(w 1, w 2)= w 1 w 2 Справедливо:
CON2(w 1, e) = U 
(w),
CON2(w 1, w 2a) = Na(CON2(w 1, w 2)), a Îå.
Согласно предложению 3.1 (iii) CON2 является примитивно рекурсивной и con 2 = [ u n (u) … n (u) ](u 2 u).
(2) Программа con n для n -местной функции CON n , n ³ 3, с CON n (w 1,…, wn)= w 1,…, wn имеет вид: con 2 (con n -1 (u 1… u n -1) u n). ð
Пример 3.4. Мы хотим представить теперь некоторые числовые функции программами. Все x,y лежат в¥.
(1) Функция следования.
Пусть Nt: ¥®¥, t ³1, – функция Nt(x)= x+t, таким образом, N1(x)=N(x) и Nt+1(x)=N(Nt(x)).
n 1 =n, n t +1 =n (n t), t ³1.
(2) Константа.
Пусть K 
:¥n®¥ – n -местная постоянная функция, причем K (x 1,…, x n)= i.
а) Нульместная константа.
k 
= c, k 
= n i(c).
b) Одноместная константа. K 
=C0, K (x +1)=U 
(K (x), x).
k = [ c u ], k 
= (n i k ).
c) n-местная константа, n ³2. K 
(x 1,…, x n)=K ( 
(x 1,…, x n)).
k 0 =k (u), k i =n i (k 0).
(3) Сумма.
SUM(0, y) = y = U (y),
SUM(x +1, y)=SUM(x, y)+1=N(SUM(x, y))=N(U 
(SUM(x, y)), x, y).
sum= [ un (u)].
(4) Произведение.
PROD(0, y)=0= K (y),
PROD(x+1,y)=SUM(PROD(x,y),y) =
=SUM(U (PROD(x, y), x, y),U 
(PROD(x, y), x, y)).
prod =[ k sum (u u 3)] = [ [ cu ][ un (u)](u [ [ u u ] u ])].
(5) Потенцирование.
EXP(0, y) = 1 = K (y),
EXP(x+1,y) = PROD(EXP(x,y),y)=
=PROD(U (EXP(x, y), x, y),U (EXP(x, y), x, y).
exp =[ k prod (uu 3)]=[ n ([ cu ])[[ cu ][ un (u)](u [[ uu ] u ])](u [[ uu ] u ])]
(6) Функция предшествования.
V(0) = 0 = C0,
V(x +1) = x = U 
(V(x), x).
v = [ c u 2] = [ c [ u u ] ].
(7) Разность.
DIFF1(0, y) = y = U (y),
DIFF1(x +1, y) =V(DIFF1(x, y)) = V(U (DIFF1(x, y), x, y);
DIFF(x, y) = DIFF1(y, x) = DIFF1(U (x, y),U (x, y).
diff1= [ uv (u)] = [ u [ c [ uu ]](u)], diff = [ u [ c [ uu ] ](u)]([ uu ] u).
(8) Факториал.
FAK(0) = 1 = K 
,
FAK(x +1) = PROD(FAK(x),N(x)) =
= PROD(U (FAK(x), x),N(U (FAK(x), x))).
fak =[ k prod (un (u 2))]=[ n (c)[[ cu ][ un (u)](u [[ uu ] u ])](un ([ uu ]))].
(9) Знак.
SGN(0) = 0 = C0,
SGN(x +1) = 1 =K (SGN(x), x).
sgn = [ c k ]=[ cn ([ cu ](u))].
Покажем теперь, что алфавит å ={ а 1,…, аk } может эффективно нумероваться с помощью биективной примитивно рекурсивной функции С k. Здесь снова речь идет о лексикографическом порядке. Мы определяем С k:å*®¥ (¥ отожествляется с а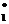 
) через
С k (e) = 0, С k (а 
,…, а 
) = 
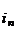ij kn-j.
Функция С k отображает биективно å n на числа между k n -1+ kn -2+…+ k +1 и kn + kn -1+…+ k2 + k, n ³ 1. Вследствие того, что
ij kn-j = k 
ij k n -1- j + in,
справедливо:
C k (e) = 0 = C0,
C k (wai) = SUM(PROD(C k (w), k) i) = N i (P k (U (C k (w), <