Цель работы: Приобретение практических навыков в разработке программ поиска безусловного экстремума функций многих переменных методом наискорейшего спуска.
Работа выполняется с использованием алгоритмических языков высокого уровня.
На работу отводится 8 часов.
Метод наискорейшего спуска - это процесс, на каждой итерации которого шаг 
выбирается из условия минимума функции 
в направлении движения:
При этом на каждой итерации необходимо решать задачу одномерной оптимизации (одномерного поиска экстремума).
Существуют различные методы одномерного поиска. Одним из наиболее эффективных методов является метод золотого сечения. Метод работает при условии, что заданная функция унимодальная на интервале, в котором имеется экстремум.
Алгоритм метода золотого сечения [3].
1. Ищется начальный отрезок 
, в котором находится экстремум:
от точки 
делается последовательная серия возрастающих шагов в направлении поиска.
При этом запоминаются 3 последние точки.
Процесс выполняется до тех пор, пока 
не будет больше, чем 
Тогда искомый интервал равен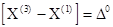 
2. Уточняется область нахождения экстремума: k:=0;
2.1. Находятся точки 
2.2. Вычисляется значение функции 
2.3. Переопределяется интервал 
и точки X1, X3:
если
если
если 
то выбирается любой из рассмотренных выше вариантов
Процедура одномерного поиска продолжается до тех пор, пока не будет достигнута заданная точность, т.е. пока Dk не будет меньше D доп.
После определения величины a (в формуле 1) методом одномерного поиска, находится новое значение многомерной точки Xk+1, в которой вновь выделяется градиент функции 
Итерационный процесс продолжается до тех пор, пока не будет достигнута требуемая точность вычисления экстремума, т.е. пока не выполнится условие: 
При небольшой размерности пространства En может быть найдено аналитическое выражение для оптимального значения a. Для этого формула (1) записывается в явном виде как функция от a: 
Затем берется производная от 
по a и приравнивается нулю. В результате решения полученного уравнения находится оптимальное значение a.
Если минимизируемая функция квадратичная, то оптимальное значение a на k - ой итерации может быть определено из векторного равенства [2]
(2)
где X1 - вектор - строка X;
- нормированный антиградиент;
- норма вектора;
H - матрица вторых производных (матрица Гессе).
Рассмотренные выше методы предполагают вычисление градиента минимизируемой функции в аналитическом виде. Если целевая (минимизируемая) функция слишком сложна, чтобы ее дифференцировать аналитически, то составляющие градиента, являющиеся частными производными по оптимизируемым переменным, аппроксимируются разностными соотношениями:
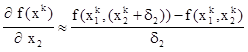(3)
где di - малые отклонения.
Для функции двух переменных для численного вычисления градиента нужно находить значения функции всего в трех точках
