А.П.Господариков, Т.Р.Акчурин, И.А.Лебедев, В.В.Тарабан
Учебно-методическое пособие дает возможность получить практические навыки при самостоятельном изучении материала и выполнении контрольных работ по темам, входящим в программу второго курса высшей математики.
Предназначено для студентов заочной формы обучения технических специальностей.
Научный редактор проф. А.П.Господариков
Рецензенты: кафедра прикладной математики (Санкт-Петербургский государственный университет путей сообщения); д-р физ.-мат. наук проф. С.И.Перегудин (Санкт-Петербургский государственный университет).
| В723 | Высшая математика. Ряды. Функции нескольких переменных. Теория вероятностей и элементы математической статистики: Учебно-методическое пособие / А.П.Господариков, Т.Р.Акчурин, И.А.Лебедев, В.В.Тарабан; Санкт-Петербургский государственный горный институт (технический университет). СПб, 2009. 113 с. |
ISBN 978-5-94211-382-7
УДК 517.52 (075.80)
ББК 22.161.1 + 22.161.6 + 22.131
| ISBN 978-5-94211-382-7 | Ó Санкт-Петербургский горный институт имени Г.В.Плеханова, 2009 |
Введение
Изучая разделы курса высшей математики, необходимо научиться исследовать сходимость рядов, использовать функциональные ряды для вычислений и решения дифференциальных уравнений, находить и использовать частные производные функций нескольких переменных, вычислять кратные и криволинейные интегралы, а также применять теорию вероятностей и обрабатывать статистический материал.
Программа
1. Числовые ряды. Признаки сходимости числовых рядов.
2. Степенные ряды. Разложение функций в степенные ряды.
3. Применение степенных рядов для приближенных вычислений.
4. Ряды Фурье и их применение (метод Фурье).
5. Частные производные и полный дифференциал функций нескольких переменных.
6. Касательная плоскость и нормаль к поверхности.
7. Частные производные высших порядков функций нескольких переменных.
8. Градиент и производная по направлению.
9. Экстремум функции нескольких переменных.
10. Наибольшее и наименьшее значения функций нескольких переменных.
11. Двойной интеграл. Вычисление двойного интеграла.
12. Двойной интеграл в полярных координатах.
13. Тройной интеграл. Вычисление тройного интеграла.
14. Тройной интеграл в цилиндрических и сферических координатах.
15. Приложения кратных интегралов (вычисление объема, массы, центра тяжести, моментов инерции).
16. Криволинейные интегралы первого и второго рода. Формула Грина.
17. Независимость криволинейного интеграла второго рода от пути интегрирования.
18. Случайные события. Основные понятия теории вероятностей.
19. Вероятность суммы событий.
20. Вероятность произведения событий.
21. Формула полной вероятности и формула Байеса.
22. Повторение независимых опытов и теоремы Лапласа.
23. Теорема Бернулли и закон Пуассона.
24. Случайные величины. Закон распределения и функция распределения.
25. Математическое ожидание случайной величины.
26. Дисперсия и среднее отклонение случайной величины.
27. Биномиальный закон распределения и закон Пуассона.
28. Равномерный и нормальный законы распределения.
29. Система двух случайных величин. Закон и функция распределения.
30. Условный закон распределения и условное математическое ожидание.
31. Начальные и центральные моменты случайной величины и системы случайных величин. Коэффициент корреляции.
32. Выборка и эмпирическое распределение. Графическое представление.
33. Точечные оценки параметров распределения по эмпирическим данным.
34. Интервальные оценки параметров распределения по эмпирическим данным.
35. Понятие о критерии согласия. Критерий Пирсона хи-квадрат.
36. Статистическая и корреляционная связь. Уравнения прямых регрессий.
37*. Векторное поле. Циркуляция, поток, дивергенция и ротор.
38. Формула Стокса и формула Остроградского. Потенциальные и соленоидальные векторные поля.
39. Операционное исчисление. Теоремы об оригиналах и изображениях.
40. Применение операционного исчисления к решению дифференциальных уравнений.
1. Ряды
1.1. Сходимость числовых рядов
Рядом называется выражение вида
 .
.
Ряд сходится, если существует конечный предел частичных сумм, образованных первыми членами ряда:

где 
Этот предел называется суммой ряда.
Если конечного предела нет, то ряд расходится. Сумму сходящегося ряда можно найти приближенно, заменяя ее на частичную сумму с достаточно большим номером:  . При этом остаток ряда
. При этом остаток ряда

позволяет оценить точность такого приближения;  при
при  .
.
Сходимость и расходимость ряда не зависит от конечного числа членов.
Необходимый признак сходимости. Если ряд  сходится, то
сходится, то  . Следовательно, если
. Следовательно, если  , то ряд
, то ряд  расходится (достаточный признак расходимости). Заметим, что необходимое условие
расходится (достаточный признак расходимости). Заметим, что необходимое условие  не является достаточным для сходимости: так, для расходящегося гармонического ряда
не является достаточным для сходимости: так, для расходящегося гармонического ряда  имеем
имеем  .
.
Для положительных рядов ( ) имеются четыре основных признака сходимости.
) имеются четыре основных признака сходимости.
Признак сравнения. 1. Пусть  (n = 1, 2, …). Если ряд
(n = 1, 2, …). Если ряд  сходится, то сходится и ряд
сходится, то сходится и ряд  ; если ряд
; если ряд  расходится, то расходится и ряд
расходится, то расходится и ряд  . 2. Ряды
. 2. Ряды  и
и  сходятся и расходятся одновременно, если
сходятся и расходятся одновременно, если  .
.
Последний предельный признак сравнения удобно применять к рядам, общий член которых зависит только от степеней переменной n. В этом случае ряд сравниваем с рядом Дирихле  , который сходится при p > 1 и расходится при p £ 1.
, который сходится при p > 1 и расходится при p £ 1.
Признак Даламбера. Если  , то при
, то при  ряд
ряд  сходится, а при
сходится, а при  ряд расходится.
ряд расходится.
Этот признак удобно применять к рядам, общий член которых зависит от степеней и показательных функций переменной n, или содержит факториалы. Напомним определение факториала:
0! = 1, 1! = 1, 2! = 1×2, 3! = 1×2×3 = 6, …, n! = 1×2× … × (n – 1) n.
Радикальный признак Коши. Если  , то при
, то при  ряд
ряд  сходится, а при
сходится, а при  – расходится.
– расходится.
Этот признак удобно применять к рядам, общий член которых зависит только от показательных функций переменной n.
Замечание. Признаки Даламбера и Коши (радикальный) не позволяют судить о сходимости ряда в случае l = 1 (требуется дополнительное исследование сходимости ряда или применение другого достаточного признака).
Интегральный признак Коши. Если непрерывная функция f (x) монотонно убывает на [1,¥) и an = f (n), то ряд  и интеграл
и интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Этот признак удобно применять к ряду, для которого нетрудно проинтегрировать функцию, задающую общий член ряда.
Пример 1. Определить сходимость или расходимость рядов:
1.  . 2.
. 2.  . 3.
. 3. 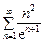 . 4.
. 4. 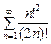 . 5.
. 5. 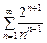 . 6.
. 6.  .
.
Решение.
1. 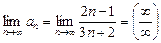

 , т.е. ряд расходится (признак расходимости).
, т.е. ряд расходится (признак расходимости).
2. Так как общий член ряда зависит только от степеней n  , то для применения признака сравнения надо определить, какой степени n эквивалентно это выражение при n ® ¥:
, то для применения признака сравнения надо определить, какой степени n эквивалентно это выражение при n ® ¥:
 .
.
Если 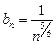 , то в силу этой эквивалентности имеем
, то в силу этой эквивалентности имеем

и по предельному признаку сравнения ряд  расходится, так как расходится ряд Дирихле
расходится, так как расходится ряд Дирихле  с показателем p = 5/6 < 1.
с показателем p = 5/6 < 1.
3. 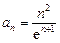 . Найдем
. Найдем  ,
,

и по признаку Даламбера ряд сходится.
4.  ,
,

 =
= 
и по признаку Даламбера ряд сходится.
5.  . Найдем
. Найдем

и по радикальному признаку ряд сходится.
6.  – непрерывная функция, убывающая на промежутке
– непрерывная функция, убывающая на промежутке  ; несобственный интеграл
; несобственный интеграл


сходится, и поэтому по интегральному признаку ряд тоже сходится.
Если для ряда  с членами аn произвольного знака сходится положительный ряд
с членами аn произвольного знака сходится положительный ряд  , из абсолютных величин его членов, то ряд называется абсолютно сходящимся. Если ряд
, из абсолютных величин его членов, то ряд называется абсолютно сходящимся. Если ряд  сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  называется условно сходящимся.
называется условно сходящимся.
Для знакочередующихся рядов  , где
, где 
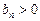 имеется следующий признак сходимости:
имеется следующий признак сходимости:
Признак Лейбница. Если для знакочередующегося ряда выполнено условие  и члены
и члены  монотонно убывают
монотонно убывают  , то ряд сходится.
, то ряд сходится.
Следствие. 
Пример 2. Определить сходимость рядов:
1.  . 2.
. 2. 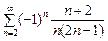 .
.
Решение. 1. Рассмотрим
 ,
,
где ряд из абсолютных величин сравним с рядом Дирихле  , который сходится (p = 2 > 1). Тогда по предельному признаку сравнения ряд
, который сходится (p = 2 > 1). Тогда по предельному признаку сравнения ряд  сходится абсолютно.
сходится абсолютно.
2.  ,
,
т.е. такой ряд сравним с гармоническим, который расходится. По предельному признаку сравнения ряд из абсолютных величин  также расходится, т.е. исходный ряд абсолютно расходится. Проверим для данного знакочередующегося ряда условия признака Лейбница:
также расходится, т.е. исходный ряд абсолютно расходится. Проверим для данного знакочередующегося ряда условия признака Лейбница:
 ,
,


члены  монотонно убывают и, следовательно, по признаку Лейбница данный ряд сходится условно.
монотонно убывают и, следовательно, по признаку Лейбница данный ряд сходится условно.
1.2. Степенные ряды. Разложение функций в степенные ряды
Важным примером функционального ряда является степенной ряд:
 ,
,
который по теореме Абеля сходится абсолютно в некотором наибольшем интервале  , называемом интервалом сходимости,где R – радиус сходимости.
, называемом интервалом сходимости,где R – радиус сходимости.
Для вычисления радиуса сходимости применяются формулы
 . (1)
. (1)
Пример 3. Найти область сходимости степенного ряда
 .
.
Решение. Чтобы определить интервал абсолютной сходимости, необходимо использовать или признаки сходимости положительных рядов, или формулы для радиуса сходимости (1). Общий член данного степенного ряда
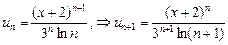 .
.
Применим признак Даламбера для определения абсолютной сходимости ряда:


 .
.
Итак, интервал сходимости – интервал (–5,1) с центром a = -2 и радиусом R = 3. Исследуем поведение степенного ряда на концах интервала. При x = 1 имеем
 .
.
Так как  и в силу расходимости гармонического ряда по признаку сравнения будет расходиться и ряд с общим членом
и в силу расходимости гармонического ряда по признаку сравнения будет расходиться и ряд с общим членом  , т.е. степенной ряд при x = 1 расходится. При x = -5 имеем
, т.е. степенной ряд при x = 1 расходится. При x = -5 имеем
 .
.
Этот знакочередующийся ряд ( ) абсолютно расходится; по признаку Лейбница
) абсолютно расходится; по признаку Лейбница 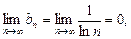 а члены ряда
а члены ряда  монотонно убывают
монотонно убывают  , поэтому данный ряд сходится (условно). Следовательно, исследуемый степенной ряд сходится на промежутке [–5,1).
, поэтому данный ряд сходится (условно). Следовательно, исследуемый степенной ряд сходится на промежутке [–5,1).
Функцию, бесконечно дифференцируемую в окрестности точки a, можно разложить в степенной ряд по степеням  . Такой ряд называется рядом Тейлора или (при a = 0) – рядом Маклорена:
. Такой ряд называется рядом Тейлора или (при a = 0) – рядом Маклорена:

 или
или  .
.
Приведем канонические разложения основных элементарных функций в ряды Маклорена:
 (2)
(2)


 (3)
(3)
 (4)
(4)
Пример 4. Разложить функцию: 1) e3 x по степеням x + 1; 2)  по степеням x; 3) ln x в окрестности точки a = 2.
по степеням x; 3) ln x в окрестности точки a = 2.
Решение. 1. В окрестности точки a = -1, используя каноническое разложение (2), имеем



где  .
.
2. В этом случае a = 0. Используя каноническое разложение (4), имеем:




 ,
,
где 
3. Используя каноническое разложение (3), имеем:



где 
Ряд сходится на интервале 
1.3. Применение степенных рядов
Разложение в степенные ряды можно использовать для приближенного вычисления значений функций, приближенного решения дифференциальных уравнений и вычисления определенных интегралов в силу того, что внутри интервала сходимости степенные ряды можно почленно многократно интегрировать и дифференцировать.
Пример 5. Вычислить с точностью D = 10–3 значение интеграла 
Решение. Используя каноническое разложение (3) и интегрируя почленно, получим:



 .
.
Этот знакочередующийся ряд удовлетворяет всем условиям признака Лейбница. Поэтому погрешность, получаемая при замене его суммы частичной суммой, не превосходит первого отброшенного члена. Найдем первый член ряда, который по абсолютной величине меньше заданной погрешности D: 


Следовательно, отбрасывая все члены ряда, начиная с четвертого, имеем

Пример 6. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения задачи Коши 

Решение. Начальное условие задано в точке a = 0, поэтому ищем решение в виде ряда Маклорена:
 .
.
Используя начальное условие и последовательно дифференцируя уравнение, можно получить значения производных от искомой функции при x = 0:
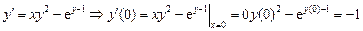 ;
;


 .
.
Так как 
 , то соответствующие члены разложения отличны от нуля и решение имеет вид
, то соответствующие члены разложения отличны от нуля и решение имеет вид
 .
.
1.4. Ряды Фурье и их применение
Функциональные ряды по тригонометрической системе функций  на промежутке
на промежутке  называются тригонометрическими рядами, или рядами Фурье. Каждая гладкая (производная непрерывная) или кусочно-гладкая функция f (x) на промежутке
называются тригонометрическими рядами, или рядами Фурье. Каждая гладкая (производная непрерывная) или кусочно-гладкая функция f (x) на промежутке  в точках непрерывности разлагается в ряд Фурье
в точках непрерывности разлагается в ряд Фурье
 (5)
(5)
где

 (6)
(6)

Если f (x) – четная функция, то
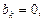


 .
.
Если f (x) – нечетная функция,то
 и
и  ,
,  . (7)
. (7)
Пример 7. Разложить в ряд Фурье функцию

Эта функция не обладает симметрией и задана на промежутке  . Находим коэффициенты ряда Фурье по формуле (6), причем интегралы по промежутку
. Находим коэффициенты ряда Фурье по формуле (6), причем интегралы по промежутку  возьмем по частям:
возьмем по частям:







Следовательно, ряд Фурье для этой функции по (5) имеет вид
 .
.
Ряды Фурье можно использовать для решения краевых задач математической физики. В качестве примера рассмотрим решение волнового уравнения колебаний струны с закрепленными концами. Движение струны описывается уравнением в частных производных:
 , (8)
, (8)
где  – отклонение точки струны с координатой x от положения равновесия в момент времени t,
– отклонение точки струны с координатой x от положения равновесия в момент времени t,  ,
,  .
.
Граничные условия для уравнения (8) (условия закрепления концов струны):
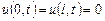 . (9)
. (9)
Начальные условия:
 , (10)
, (10)
где функции f (x) и g (x)задают начальную форму струны и начальное распределение скоростей соответственно. Это – краевая задача.
Решение поставленной задачи ищем в виде ряда Фурье по синусам для x и с коэффициентами от t (метод Фурье):
 (11)
(11)
Краевые условия (9) при этом удовлетворяются автоматически, так как  при x = 0, l. Подставляя (11) в уравнение (8), получим:
при x = 0, l. Подставляя (11) в уравнение (8), получим:
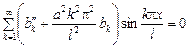 ,
,
откуда  . Решение данного уравнения имеет вид
. Решение данного уравнения имеет вид 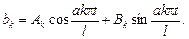
Таким образом,
 (12)
(12)
Постоянные  и
и  находим из начальных условий (10). Имеем
находим из начальных условий (10). Имеем
 ,
,  .
.
Отсюда следует, что  и
и  являются коэффициентами Фурье функций f (x) и g (x)в их представлении тригонометрическими рядами Фурье по синусам. Поэтому по (7)
являются коэффициентами Фурье функций f (x) и g (x)в их представлении тригонометрическими рядами Фурье по синусам. Поэтому по (7)

 (13)
(13)
Таким образом, решением задачи является функция (12), где коэффициенты  и
и  определяются формулами (13).
определяются формулами (13).
Отметим, что любую функцию, заданную на  , можно разложить в ряд Фурье по косинусам (как четную) или по синусам (как нечетную).
, можно разложить в ряд Фурье по косинусам (как четную) или по синусам (как нечетную).
2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2.1. Частные производные и дифференциалы функций нескольких переменных
Производные функции нескольких переменных вычисляют отдельно по каждому из аргументов (остальные аргументы при этом полагают постоянными) и называют частными производными. В свою очередь, от них, как от функций нескольких переменных, можно снова находить частные производные, которые будут уже частными производными второго порядка, и т.д.
Например, для функции  имеем
имеем
 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
 .
.
Если функция  и все ее частные производные второго порядка непрерывны, то
и все ее частные производные второго порядка непрерывны, то  , т.е. смешанные (по разным переменным) частные производные не зависят от порядка дифференцирования (теорема Шварца).
, т.е. смешанные (по разным переменным) частные производные не зависят от порядка дифференцирования (теорема Шварца).
Полный дифференциал – это главная часть полного приращения функции нескольких переменных, линейная относительно приращений аргументов. Полный дифференциал функции 
 ,
,
где  .
.
Функция дифференцируема, если она имеет дифференциал. Достаточным условием этого является непрерывность частных производных первого порядка.
Применение дифференциала в приближенных вычислениях основано на том, что он является главной частью приращения функции, поэтому справедливы приближенные равенства:  и
и 
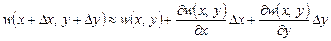 . (14)
. (14)
Если приращения аргументов имеют смысл абсолютных погрешностей аргументов, то с помощью дифференциала можно оценить абсолютную (D) или относительную (d) погрешность вычисления функции:
 ;
;  .
.
Пример 8. Вычислить приближенное значение функции  в точке B (4,03; 1,96), исходя из ее значения в точке A (4,2) и заменив приращение функции дифференциалом. Найти возникающую при этом относительную погрешность (в процентах).
в точке B (4,03; 1,96), исходя из ее значения в точке A (4,2) и заменив приращение функции дифференциалом. Найти возникающую при этом относительную погрешность (в процентах).
Решение. В данном случае  ,
,  ,
,  ,
,
 .
.
По (14) приближенное значение функции в точке B
 .
.
Так как точное значение функции в точке B
 ,
,
то абсолютная и относительная погрешности равны соответственно:

 0,04 %.
0,04 %.
Формула производной сложной функции нескольких переменных, если  и
и  , имеет вид
, имеет вид
 .
.
Если функция одной переменной  задана неявно уравнением
задана неявно уравнением 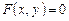 , то ее производная
, то ее производная
 ,
,
где  ,
,  .
.
Частные производные функции двух переменных  , заданной неявно уравнением
, заданной неявно уравнением  , имеют вид
, имеют вид
 ,
,
где  .
.
Аналогичные выражения справедливы для производных неявно заданной функции от любого числа переменных.
Градиент функции  – вектор, компонентами которого являются соответствующие частные производные
– вектор, компонентами которого являются соответствующие частные производные
 .
.
Градиент функции б©льшего числа переменных определяется аналогично. Градиент в данной точке перпендикулярен проходящей через эту точку линии  или поверхности
или поверхности  уровня одинаковых значений функции.
уровня одинаковых значений функции.
Производная функции  или
или 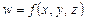 в точке M по направлению l (т.е. скорость изменения значений функции при движении в данном направлении) равна скалярному произведению градиента функции в точке M и единичного вектора, задающего направление
в точке M по направлению l (т.е. скорость изменения значений функции при движении в данном направлении) равна скалярному произведению градиента функции в точке M и единичного вектора, задающего направление  :
:

 .
.
Градиент задает направление наибольшего роста значений функции в данной точке, и производная по направлению градиента равна модулю градиента.
Пример 9. Дана функция  . Найти скорость и направление максимального роста функции в точке M (2,1,0) и производные по направлению от точки М к точке N (1,2,2) и по направлению
. Найти скорость и направление максимального роста функции в точке M (2,1,0) и производные по направлению от точки М к точке N (1,2,2) и по направлению 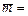 {2,1 – 2}.
{2,1 – 2}.
Решение. Так как

 ,
,
то направление максимального роста и его скорость

 .
.
Направление от точки M к N задается вектором

 .
.
Производная по этому направлению
 ,
,
т.е. функция убывает в этом направлении.
Для направления, заданного вектором 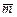 , имеем
, имеем
 ,
,
а производная по этому направлению
 ,
,
т.е. функция возрастает в этом направлении.
Если поверхность S задана неявно уравнением  , то уравнение касательной плоскости к этой поверхности в точке
, то уравнение касательной плоскости к этой поверхности в точке  имеет вид
имеет вид
 ,
,
а уравнение нормали (т.е. прямой, перпендикулярной касательной плоскости) имеет вид

2.2. Экстремум функций нескольких переменных
Точки, в которых все частные производные функции обращаются в нуль или не существуют, являются подозрительными на экстремум (необходимое условие экстремума). Достаточные условия экстремума формулируются для функций любого числа переменных, но мы рассмотрим только случай функции двух переменных  : если в стационарной точке M (где все частные производные первого порядка равны нулю) найдены значения вторых частных производных
: если в стационарной точке M (где все частные производные первого порядка равны нулю) найдены значения вторых частных производных
 , то
, то
1) если дискриминант  , то в точке M есть экстремум, причем максимум при A < 0 и минимум при A > 0;
, то в точке M есть экстремум, причем максимум при A < 0 и минимум при A > 0;
2) если 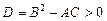 , то в точке M нет экстремума;
, то в точке M нет экстремума;
3) если  , то необходимо дополнительное исследование.
, то необходимо дополнительное исследование.
Пример 10. Найти экстремум функции  .
.
Решение. Находим стационарные точки:

Найдем решения первого уравнения и подставим их во второе:
 ;
;
 .
.
Таким образом, стационарными точками являются точки:

Определим вторые частные производные:
 ;
;
 ;
;
 .
.
Для первой и второй стационарных точек  и
и 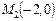 соответственно имеем
соответственно имеем
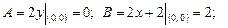
 ;
;
 ;
;
 .
.
Так как  , то экстремума нет.
, то экстремума нет.
Для третьей и четвертой стационарных точек  и
и  соответственно имеем
соответственно имеем
 ;
;
 ;
;
 ;
;
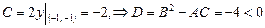 .
.
Так как  , то в точках M 3 и M 4 есть экстремум, причем
, то в точках M 3 и M 4 есть экстремум, причем  и
и  .
.
2.3. Оптимизация функций нескольких переменных
Для отыскания наибольшего или наименьшего значения функций нескольких переменных в ограниченной замкнутой области достаточно найти значения этой функции в подозрительных на экстремум точках внутри области и сравнить с ее наибольшим и наименьшим значениями на границе области.
Пример 11. Найти наибольшее и наименьшее значения функции  в области
в области  и
и  .
.
Решение. Область ограничена линиями х = –2, х = 0,  и представляет собой треугольник, ограниченный тремя линиями L 1, L 2 и L 3 (рис.1).
и представляет собой треугольник, ограниченный тремя линиями L 1, L 2 и L 3 (рис.1).
Найдем стационарные точки:

Точка (–1/4,1/4) лежит внутри области  .
.
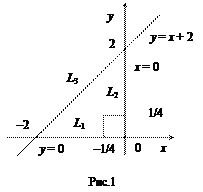
|
Исследуем функцию на наибольшее и наименьшее значения на границе области. Уравнение линии L 1 есть y = 0, где –2 £ х £ 0 и на L 1 функция z – функция только переменной x, заданная на отрезке [–2, 0]:
 .
.
Производная  при
при  и
и 
 .
.
Значения функции z 1 на концах отрезка [–2, 0]: 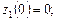
 .
.
Уравнение линии L 2 есть  где 0 £ y £ 2, и на L 2 функция z – функция только переменной y, заданная на отрезке [0, 2]:
где 0 £ y £ 2, и на L 2 функция z – функция только переменной y, заданная на отрезке [0, 2]:
 .
.
Производная  при
при  . Значения функции z 2 на концах этог
. Значения функции z 2 на концах этог