Эту аксиому часто называют законом независимости действия сил или принципом суперпозиции.
Под действием нескольких сил материальная точка приобретает ускорение, равное геометрической сумме ускорений, которые бы имела точка под действием каждой силы в отдельности.
Согласно аксиоме, несколько сил (F1, F2,..., Fn), действующих на материальную точку, можно заменить одной силой F = F1 + F2 +... + Fn, то есть она аналогична аксиоме параллелограмма сил в статике.
I закон Ньютона
Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.
II закон Ньютона
Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:
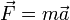
III закон Ньютона
Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.


Билет №18
1.Система сходящихся сил. Условие равновесия.
Система сходящихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке.
Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух (а не трёх, как в других статически определимых системах). Это обусловлено тем, что у такой системы сил имеется равнодействующая, равная нулю, и её момент равен нулю относительно любой точки плоскости по теореме Вариньона, а не исходя из условий равновесия статики.
В трёхмерном пространстве сходящаяся система сил является статически определимой, если число неизвестных сил в ней не превышает трёх.
На практике простейшим примером сходящейся системы сил являются силы, действующие на груз, лежащий на абсолютно гладком, горизонтальном столе. В такой системе сил имеется сила тяжести, и сила реакции опоры, действующие вдоль одной линии. Другим примером сходящейся системы сил являются силы, действующие в точке подвеса груза, висящего на двух тросах (см. рисунок).

Задачи с системой сходящихся сил могут быть решены как аналитически, так и графически (методами графостатики).

F1, F2,...,Fn)~R => для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут (рис.). Это условие используется при графическом решении задач для плоских систем сил. Векторное равенство R=0 эквивалентно трем скалярным равенствам: Rx=åFkx=F1x+F2x+…+Fnx=0; Ry=åFky=F1y+F2y+…+Fny=0; Rz=åFkz=F1z+F2z+…+Fnz=0; где Fkx, Fky, Fkz– проекции силы Fkна оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.
2.Первая задача динамики.
В основе классической динамики лежат законы, впервые сформулированные и систематически изложенные И.Ньютоном в его «Математических началах натуральной философии».
В зависимости от того, что нам известно и что необходимо найти, в динамике рассматривают две основные задачи.
Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.
При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки

где m – масса точки;
a – ускорение точки;
Fi – силы, действующие на точку.
В зависимости от способа задания движения точки, это уравнение можно записать по-разному.
Для векторного способа задания движения

где r = r (t) – радиус-вектор, определяющий положение точки по отношению к выбранной системе отсчета.
Для координатного способа задания движения точки

где x = x (t), y = y (t), z = z (t) – координаты точки, заданные как функции времени.
Для естественного способа задания движения точки

0 = Σ Fib,
где dV/ dt – проекция ускорения точки на касательную в данной точке (касательное ускорение), V2/ ρ – проекция ускорения на нормаль (нормальное ускорение),
ρ – радиус кривизны траектории.
В правой части уравнений – проекции сил на касательную ΣFiτ,
нормаль ΣFin и бинормаль ΣFib.
По заданному закону движения точки определяются правые части этих уравнений, и далее может быть определена результирующая сила
– при координатном способе задания движения:
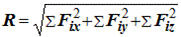
– при естественном способе или одна из составляющих сил:

Направление силы определяется с помощью направляющих косинусов:
cos (α) = Rx / R, cos (β) = Ry / R, cos (γ) = Rz / R
где α, β, γ – углы между направлением силы и осями x, y, z соответственно.
Аналогично определяются углы, которые составляют силы с естественными осями координат.

Билет №19
1.Диаграмма растяжения.
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F - продольная растягивающая сила, [Н];
Δl - абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I - участок пропорциональности;
II - участок текучести;
III - участок самоупрочнения;
IV - участок разрушения.
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова "идет вверх" (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая "шейка", вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Рис. 2 Стальной образец с "шейкой"
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы "идет вниз".
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована "шейка"
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax ⋅ Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
2.Вращательное движение твердого тела. Закон движения.
Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П, одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.
Угловое ускорение – мера изменения угловой скорости:

Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида

Закон движения может быть найден, в зависимости от задачи, либо из дифференциальных законов механики, либо из интегральных, либо из так называемых вариационных принципов.

Билет №20
1.Оценка прочности.
Прочность — свойство материала сопротивляться разрушению под действием внутренних напряжений, возникающих под воздействием внешних сил.
Свойство конструкции выполнять назначение, не разрушаясь в течение заданного времени.
Прочность подразделяют на статическую, под действием постоянных нагрузок, динамическую и усталостную (выносливость), имеющую место при действии циклических переменных нагрузок.
Для конструкций различают общую прочность — способность всей конструкции выдерживать нагрузки без разрушения, и местную — та же способность отдельных узлов, деталей, соединений.
В настоящее время при расчёте на прочность используют как расчёт по допускаемым напряжениям, так и расчёт по допускаемому числу циклов нагружения. Основные неравенства расчёта по допускаемым напряжениям:

где
 и
и  — наибольшие расчётные нормальное и касательное напряжения, соответственно;
— наибольшие расчётные нормальное и касательное напряжения, соответственно;
 и
и  — допускаемые нормальное и касательное напряжения, безопасные для прочности детали.
— допускаемые нормальное и касательное напряжения, безопасные для прочности детали.
2.Правила сложения ускорения в сложном движении.
Дифференцируя по времени выражение  , получаем
, получаем
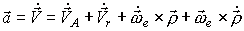
| (1) |
В выражении (1) V' = aA является ускорением начала подвижной системы координат; ωe = εe является угловым ускорением переносного движения или угловым ускорением вращения подвижной системы координат в неподвижной. Векторы Vr и ρ известны в проекциях на оси подвижной системы координат и изменяются по величине и направлению, поэтому, согласно теореме об абсолютной производной вектора,

| (2) |
В выражениях (2) локальная производная вектора скорости характеризует быстроту его изменения в подвижной системе координат и является относительным ускорением. Таким образом, из (1) имеем

| (3) |
Для выделения переносного ускорения используем прием останова, принимая в (3) ar = 0 и Vr = 0. Когда точка остановлена в подвижной системе координат (вморожена в подвижную систему координат), она за счет движения подвижной системы координат переносится относительно неподвижной, и ее абсолютное ускорение равно переносному ускорению a = ae. Учитывая это, из (3) получаем
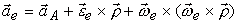
| (4) |
то есть переносное ускорение совпадает с ускорением той точки подвижной системы координат, где в данное мгновение времени находится материальная точка, если принять подвижную систему координат за твердое тело. Картина движения будет нагляднее, если подвижный трехгранник Ox1y1z1 на рис. 105 принять за ледяной трехгранник, где в данный момент времени, в данном положении вморожена точка M.
Подставляя выражение (4) в (3), имеем

| (5) |
Последнее слагаемое в (5) называется кориолисовым ускорением и обозначается ac. Таким образом, имеем математическую запись теоремы:

| (6) |
которую можно сформулировать так: абсолютное ускорение точки, участвующей в сложном движении, равно геометрической сумме относительного, переносного и кориолисова ускорений.
Остановимся на кориолисовом ускорении, равном

| (7) |
Величина кориолисова ускорения вычисляется по формуле

| (8) |
 а направление вектора определяется по правилу построения вектора векторного произведения векторов ωe и Vr (рис. a). Когда переносное и относительное движение лежат в одной плоскости, построение вектора кориолисова ускорения облегчается применением правила Н.Е. Жуковского. В этом случае для нахождения направления кориолисова ускорения достаточно повернуть вектор относительной скорости на угол 90° в сторону переносного вращения (рис. b).
а направление вектора определяется по правилу построения вектора векторного произведения векторов ωe и Vr (рис. a). Когда переносное и относительное движение лежат в одной плоскости, построение вектора кориолисова ускорения облегчается применением правила Н.Е. Жуковского. В этом случае для нахождения направления кориолисова ускорения достаточно повернуть вектор относительной скорости на угол 90° в сторону переносного вращения (рис. b).
На основании формулы (8) можно указать следующие случаи, когда кориолисово ускорение равно нулю: 1) ωe = 0; 2) ωe//Vr; 3) Vr = 0. Второй и третий случаи могут возникать в процессе движения, но особого интереса не представляют. Первый случай имеет место, когда переносное движение поступательное, и часто встречается при решении конкретных вопросов теории и практических задач.

Билет №21
1.Сила. Координатный способ задания сил.
Сила в механике, величина, являющаяся мерой механического действия на данное материальное тело других тел. Это действие вызывает изменение скоростей точек тела или его деформацию и может иметь место как при непосредственном контакте (давления прижатых друг к другу тел, трение), так и через посредство создаваемых телами полей (поле тяготения электромагнитное поле). Сила (в механике) — величина векторная и в каждый момент времени характеризуется её численным значением, направлением в пространстве и точкой приложения; сложение Сила (в механике) производится по правилу параллелограмма.
Прямая, вдоль которой направлена Сила (в механике), называется линией действия Сила (в механике) Если тело можно рассматривать как недеформируемое (абсолютно твердое), то Сила (в механике) можно считать приложенной к любой точке на ее линии действия. Действующая на частицу Сила (в механике) может быть постоянной (Сила (в механике) тяжести), а может определенным образом зависеть от времени (переменное электромагнитное поле), от положения частицы в пространстве (Сила (в механике) тяготения) и от скорости частицы (Сила (в механике) сопротивления среды).
Измерение Сила (в механике) производят статическими или динамическими методами. Статический метод основан на уравновешивании измеряемой Сила (в механике) другой, ранее известной. Динамический метод основан на законе Динамики mw = F, позволяющем, если известна масса т тела и измерено ускорение w его свободного поступательного движения относительно инерциальной системы отсчета, найти силу F. Единицами измерения С служат ньютон (н) и дина (дин); 1 дин = 10-5 н и 1 кгс » 9,81 н.
В прямоугольной системе координат XYZ (рис.) сила  задается модулем
задается модулем  , углами QUOTE
, углами QUOTE 
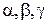 , образованными силой
, образованными силой  с осями координат и точкой приложения силы (точка А). Положение точки А определяется координатами
с осями координат и точкой приложения силы (точка А). Положение точки А определяется координатами  . Углы QUOTE
. Углы QUOTE 
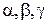 называются направляющими углами.
называются направляющими углами.
Если же заданы проекции силы 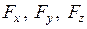 , то модуль силы и косинусы направляющих углов определятся по следующим формулам:
, то модуль силы и косинусы направляющих углов определятся по следующим формулам:
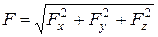


2.Закон изменения момента количества движения.
Разделяя силы, действующие на точки системы, на внешние и внутренние, запишем для каждой точки системы теорему об изменении момента количества движения относительно неподвижного центра O:

Суммируя между собой правые и левые части полученных выражений, вынося производную за знак суммы, получаем

| (1) |
так как главный момент внутренних сил системы равен нулю.
Сумму моментов количеств движений материальных точек системы относительно неподвижного центра O назовем моментом количеств движений системы материальных точек или кинетическим моментом системы относительно центра O и обозначим KO, то есть

| (2) |
Тогда из последнего выражения в (1) следует

| (3) |
то есть теорему об изменении момента количеств движения системы материальных точек в дифференциальной форме можно сформулировать так: производная по времени от момента количеств движения (кинетического момента) системы относительно неподвижного центра равна главному моменту внешних сил системы относительно того же центра.
Векторной записи теоремы соответствуют три скалярных выражения записи теоремы в проекциях на оси инерциальной системы координат Oxyz, которая считается неподвижной:

| (4) |
где Kx, Ky, Kz - моменты количеств движения системы относительно осей координат, а Mxe, Mye, Mze - суммы моментов всех внешних сил системы относительно тех же осей.
Теорема имеет интегральную форму, которую часто называют теоремой момента импульсов. Теорема об изменении момента количеств движения в интегральной форме редко используется в решении задач динамики материальной системы и здесь не рассматривается. Отметим, что она чаще применяется в механике сплошной среды, в теории удара и что на ее основе доказывается теорема Резаля, которая применяется в приближенной теории гироскопа.

Билет №22
1.Внутренние усилия, напряжения, деформации и связь между ними.
Силы, которые действуют на изделие, можно подразделить на внешние и внутренние.
Внешние силы возникают от внешней нагрузки: вес изделия, давление газа в сосуде, вес снега на крыше здания, сейсмические воздействия и др. Внутренние силы возникают от изменения структуры металла под действием внешней нагрузки или при сварке, от изменения температуры изделия при эксплуатации и т. п. При расчетах на прочность внутреннюю силу часто называют усилием.
Внешние нагрузки могут быть статическими, то есть постоянными по величине и направлению, динамическими (то есть переменными) и ударными. Динамические знакопеременные нагрузки называют также вибрационными.
Деформацией называется изменение формы и размеров тела под действием внешней или внутренней силы.
Рассмотрим удлинение стержня длиной L, к которому приложены силы, возрастающие от Р до Pv растягивающие его.
Под действием этих сил стержень удлиняется. Обозначим через L удлинение стержня (такое удлинение называется абсолютным удлинением). При растяжении стержня постоянного сечения величина деформации определяется действующей силой и будет тем больше, чем больше приложенная сила. Напряжением называют силу, отнесенную к единице площади поперечного сечения тела. Так как сила измеряется в кгс, а поперечное сечение в мм2 или в см2, то напряжение будет выражаться в кгс/мм2. Различают напряжения, возникающие при растяжении, сжатии, изгибе, кручении и срезе. Величину напряжения растяжения находят по формуле: А> — где 8р — напряжение растяжения (выраженное в кгс/мм2); Р — растягивающая сила, кгс; F — площадь поперечного сечения детали до ее разрушения, мм2. Деформации бывают упругие и пластические. Если форма и размеры тела восстанавливаются после прекращения действия силы, то такая деформация называется упругой. Если же деформация остается и после снятия нагрузки, то такая деформация называется пластической.
2.Плоскопараллельное движение твердого тела.
Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 1).
При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M1M2) совершают одинаковые движения.

Рисунок 1

Рисунок 2
Отрезок M1M2 движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.
На рисунке 2 показано перемещение пластинки в плоской системе отсчета xOy из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A с последующим поворотом на угол φ вокруг точки A1. Это же перемещение можно выполнить иначе.
Например, перемещая пластинку поступательно с траекторией точки B, с последующим поворотом вокруг B1 на угол φ. Траектории точек A и B различны, а угол поворота в обоих случаях одинаков.
Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:
xA=xA(t), yA=yA(t), φ=φ(t).
Точка A в этом случае называется полюсом. Если принять за полюс точку B, то получим уравнения:
xB=xB(t), yB=yB(t), φ=φ(t)
За полюс выбирается точка, закон движения которой известен.

Билет №23
1.Напряжения при растяжении и сжатии стержня.
При растяжении-сжатии стержня с постоянными поперечными размерами в любом поперечном сечении возникают нормальные напряжения, равномерно распределенные по сечению и равные
o = N/A
где N - продольная сила в сечении;
А -площадь поперечного сечения.
Эта формула справедлива только для поперечных сечений, отстоящих от места приложения нагрузки на расстоянии не меньшем поперечного размера стержня (принцип Сен-Венана).
Вблизи места приложения нагрузки напряжения распределяются
неравномерно.
В случае однородного стержня, растянутого или сжатого силами, приложенными на концах, напряжения остаются постоянными как по сечению, так и по длине, т.е. одинаковы для всех точек объема стержня
Такое напряженное состояние в сопромате называется однородным.
Продольную деформацию стержня характеризуют следующие величины (рис. 5).
Абсолютная продольная деформация (удлинение при растяжении и укорочении при сжатии) ^ l = l1-l
где 1 -первоначальная длина стержня;
l1 - конечная длина.
 Относительная продольная деформация (относительное удлинение). e = ^ l / l
Относительная продольная деформация (относительное удлинение). e = ^ l / l
Поперечную деформацию стержня в сопротивление материалов характеризуют следующие величины:
Абсолютная поперечная деформация ^b = b – b1,
где b -первоначальный поперечный размер,
b1 - поперечный размер после деформации
Относительная поперечная деформация e 1 = ^b / b
При растяжении продольную деформацию можно считать положительной (е > 0), а поперечную отрицательной (е 1 < 0).
При сжатии, наоборот e < 0, е 1 > 0.
Абсолютная величина отношения e1 к е называется коэффициентом Пуассона,
M = [e1/e]
Коэффициент Пуассона M (мю) - величина безразмерная и его значение
для различных материалов колеблется в пределах от 0 до 0,5. Объемная деформация характеризуется относительным изменением объема
ev = ^V / V
где ^V - абсолютное изменение объема;
V - Первоначальный объем стержня.
Закон Гука о = e Е,
где Е - коэффициент пропорциональности, называемый модулем продольной упругости, который имеет размерность Па, кПа, мПа.
Закон Гука справедлив, пока напряжения не превосходят определенной для каждого материала величины, называемой пределом пропорциональности.
Абсолютное удлинение стержня постоянного сечения при постоянном по его длине значении продольной силы определяется по формуле: ^l = Nl / EA - закон Гука
где ЕА – жесткость сечения. Эта формула очень важна в курсе изучения сопротивления материалов вообще и в решении задач по сопромату в частности.
2.Ускорение кориолиса.
Ускорение кориолиса (поворотное ускорение) - добавочное ускорение  , к-рое точка получает при т. н. сложном движении, когда подвижная система отсчёта перемещается не поступательно. К. у. учитывает влияние переносного движения (движения подвижной системы отсчёта) на изменение относит. скорости точки
, к-рое точка получает при т. н. сложном движении, когда подвижная система отсчёта перемещается не поступательно. К. у. учитывает влияние переносного движения (движения подвижной системы отсчёта) на изменение относит. скорости точки  и влияние относит. движения точки на изменение её переносной скорости. Вектор
и влияние относит. движения точки на изменение её переносной скорости. Вектор  и его модуль вычисляются соответственно по ф-лам
и его модуль вычисляются соответственно по ф-лам  и
и  =
=  , где
, где  - угл. скорость поворота подвижной системы отсчёта относительно неподвижной,
- угл. скорость поворота подвижной системы отсчёта относительно неподвижной,  - угол между
- угол между  и
и 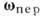 . Направление К. у. можно найти, спроектировав вектор
. Направление К. у. можно найти, спроектировав вектор  на плоскость, перпендикулярную к
на плоскость, перпендикулярную к  , и повернув эту проекцию на 90° в сторону переносного вращения. Напр., у точки, движущейся в северном полушарии вдоль поверхности Земли с севера на юг, К. у., обусловленное суточным вращением Земли, направлено на восток.
, и повернув эту проекцию на 90° в сторону переносного вращения. Напр., у точки, движущейся в северном полушарии вдоль поверхности Земли с севера на юг, К. у., обусловленное суточным вращением Земли, направлено на восток.
Следует подчеркнуть, что К. у. точки - это часть её абс. ускорения, т. е. ускорения по отношению к основной (неподвижной) системе отсчёта, а не по отношению к подвижной. Так, напр., при движении вдоль поверхности Земли точка будет иметь К. у. по отношению к звёздам, а не к Земле.
К. у. отсутствует, когда переносное движение является поступательным (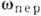 =0) или когда относит. движение происходит вдоль прямой, параллельной оси переносного вращения (
=0) или когда относит. движение происходит вдоль прямой, параллельной оси переносного вращения ( ). Понятием К. у. пользуются в кинематике при определении полного ускорения точки по ускорениям составных движений, а также в динамике при изучении относит. движения.
). Понятием К. у. пользуются в кинематике при определении полного ускорения точки по ускорениям составных движений, а также в динамике при изучении относит. движения.

Билет №24
1.Правила сложения сил. Равнодействующая системы сходящихся сил.



Сложение сил производится по правилам сложения векторов. Пусть есть две силы: f1 и f2. Надо найти их сумму.
Перенесем по правилу сложения векторов начало второго вектора в конец первого.
Соединим начало первого вектора с концом второго. Полученный вектор - искомая сумма.

Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Докажем теорему: Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия. Пусть задана система сходящихся сил F1, F2, F3,..., Fn, приложенных к абсолютно твердому телу (рис. а). Перенесем точки приложения сил по линиям их действия в точку пересечения этих линий (б). Получили сист сил, прил к одной точке. Она эквивалентна заданной. Сложим F1 и F2, получим их равнодействующую: R2=F1+F2. Сложим R2 с F3: R3=R2+F3=F1+F2+F3. Сложим F1+F2+F3+…+Fn=Rn=R=åFi. Ч.т.д. Вместо параллелограммов можно построить силовой многоугольник. Пусть система состоит из 4 сил (рис 2.). От конца вектора F1 отложим вектор F2. Вектор, соединяющий начало О и конец вектора F2, будет вектором R2. Далее отложим вектор F3 помещая его начало в конце вектора F2. Тогда мы получим вектор R8, идущий от точки О к концу вектора F3. Точно так же добавим вектор F4; при этом получим, что вектор, идущий от начала первого вектора F1 к концу вектора F4, является равнодействующей R. Такой пространственный многоугольник называется силовым. Если конец последней силы не совпадает с началом первой силы, то силовой многоугольник наз разомкнутый. Если для нах равнодействующей исп прав геометр, то этот способ наз геометрическим.

Больше пользуются аналитическим способом для определения равнодействующей. Проекция суммы векторов на некоторую ось равна сумме проекций на ту же ось слагаемых векторов, получим Rx=åFkx=F1x+F2x+…+Fnx; Ry=åFky=F1y+F2y+…+Fny; Rz=åFkz=F1z+F2z+…+Fnz; где Fkx, Fky, Fkz– проекции силы Fk на оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на соответствующие оси. Модуль равнодействующей R равен: R=(Rx2+Ry2+Rz2)1/2. Направляющие косинусы равны: cos(x,R)=Rx/R, cos(y,R)=Ry/R, cos(z,R)=Rz/R. Если силы распол в пл-ти то всё аналогично, отсутствует ось Z.
2.Способы задания закона движения и связь между ними.
Способы задания движения точки: 1)естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении.
Естественный сп.указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t)– закондвижения точки. При прямолинейном движении: х=f(t).
Координатный сп.положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t).
Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).
Векторный сп. положение точки определяется ее радиус-вектором, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е.траектория – годограф радиус-вектора. Связь между координатным и векторным способами:,
(– орты – единичные вектора, сонаправленные с какой-либо осью)
модуль, направляющие косинусы: и т.д.
Переход от координатного способа к естественному:.
Скорость точки.Вектор ск-сти: – первая производная от радиус-вектора по времени (точка обозначает производную по времени);. Проекции скорости:,,. Модуль скорости:
, направляющие косинусы: и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным. При естественном сп.: – модуль скорости,вектор скорости:, – орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление, поперечное направление, модуль скорости; x=rcosj, y=rsinj.
Ускорение точки., [м/сек2]. Проекции уск.-я: и т.д. Модуль уск.-я:, направляющ.косинусы:, и т.д.
При задании движения в полярных координатах: проекции ускорения на радиальное направление, поперечное направление, модуль ускорения. При естественным сп. задания движения