Глава 1. Выборочный метод.

 

§1. Основные задачи математической статистики.

 

Математическая статистика занимается разработкой методов сбора и анализа эк­спериментальных данных, полученных в результате наблюдения массовых случайных явлений с целью выявления закономерностей, которым подчинены эти явления.

Основные методы и приёмы рассуждений в математической статистике – те же са­мые, что и в теории вероятностей, т.к. задачи математической статистики в известной мере являются обратными задачам теории вероятностей.

В теории вероятностей математическая модель считается заданной, требуется найти вероятности событий, законы распределения случайных величин и их числовые характеристики.

В математической статистике исходят из известных реализаций случайных собы-тий, называемых статистическими данными. Математическая статистика разрабатывает методы, которые позволяют по этим статистическим данным подобрать подходящую теоретико-вероятностную модель.

Перечислим основные задачи, которые решает математическая статистика:

1. Определение закона распределения случайной величины по статисти-чес­ким данным.

2. Проверка статистических гипотез. Например, согласуются ли экспери-мен­тальные данные с гипотезой о том, что случайная величина имеет за­кон распределения с функцией распределения F (x). Являются ли случай­ная величина X и случайная величина Y независимыми.

3. Статистическое оценивание параметров распределения.

 

§2. Генеральная совокупность и выборка.

 

Пусть имеется совокупность однородных объектов. Изучается распределение ка-кого-либо признака, характеризующего эти объекты. Например: если есть партия дета-лей, то таким признаком может быть стандартность, вес, геометрические размеры и т.д.

Изучаемый признак является случайной величиной, значение которой меняется от объекта к объекту. Чтобы составить представление о распределении этой случайной величины или её числовых характеристиках, нет необходимости обследовать каждый объект совокупности. Это физически невозможно, если совокупность содержит большое число объектов, кроме того, проведение каждого эксперимента может быть связано с его дороговизной и сложностью. Поэтому отбирают из всей генеральной совокупности огра-ниченное число объектов и подвергают их изучению. Совокупность объектов, из которых производится выборка, или весь мыслимый набор наблюдений, описывающих случайную величину, называется генеральной совокупностью. Генеральная совокупность – это гене-ральная случайная величина X (e) и связанное с ней вероятностное пространство (E, K, P).

Генеральная совокупность может содержать конечное число или бесконечное число элементов.

Случайно отобранные из генеральной совокупности объекты или совокупный ре-зуль­тат n независимых наблюдений за генеральной случайной величиной называется выборкой.

Различают выборку конкретную и случайную.

Конкретная выборка – это конкретный набор чисел x₁, x₂, …, x_n, полученных в ре-зуль­тате n независимых наблюдений над случайной величиной X.

Случайная выборка – это весь мыслимый набор конкретных выборок или последо-ва­тельность X₁, X₂, …, X_n случайных величин, независимых, одинаково распределённых, и рас­пределение каждой из этих случайных величин совпадает с распределением гене-раль­ной случайной величины X (e).

Пусть имеется куча камней, каждый камень имеет конкретный вес, т.е. вес камня – есть случайная величина X (e). Выберем из этой кучи n камней, найдём x₁, x₂, …, x_n – веса камней (конкретная выборка).

Расположим числа (*) в порядке возрастания их веса

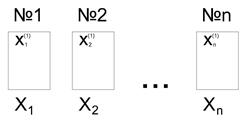
Повторив процедуру, мы можем получить k конкретных выборок типа (*). В ящик №1 – самые лёгкие камни, №2 – более тяжёлые, …, № n – самые тяжёлые. В результате веса камней в каждом ящике будут являться случайными величинами, независимыми, одинаково распределёнными. В этом случае мы имеем случайную выборку: X₁, X₂, …, X_n. Сущность выборочного метода состоит в том, что по выборке, как по некоторой части генеральной совокупности, делается вывод о генеральной совокупности в целом.

 

§3. Повторные и бесповторные выборки. Репрезентативная вы­борка.

 

Повторной называют выборку, при которой объект перед выбором следующего воз­вращается в генеральную совокупность.

Бесповторная выборка – отобранный объект в генеральную совокупность не возвраща­ется.

Оказывается, результаты выборки зависят не только от её объёма, но и от способа от­бора объектов.

Выбор должен быть таким, чтобы он правильно представлял интересующий нас при­знак генеральной совокупности. В этом случае выборку называют репрезентативной (представительной). Можно показать, что в силу закона больших чисел можно утверж-дать, что выборка будет репрезентативной, если её осуществлять случайно. Выборка бу-дет осуществлена случайно, если все объекты имеют одинаковую вероятность попасть в выборку. На практике обычно пользуются бесповторным случайным отбором.

 

§4. Статистическое распределение выборки.

 

Пусть из генеральной совокупности извлечена выборка и изучается случайная вели­чина X, при этом значение x₁ наблюдалось n₁ раз, x₂ – n₂ раз, …, x_k – n_k раз.

- объём выборки.

Наблюдаемые значения x_i (x₁, x₂, …, x_k) называются вариантами, а последователь-ность вариант, записанных в возрастающем виде, называется вариационным рядом. Числа наблюдений n_i называют частотами, а их отношения к объёму выборки – относитель­ными частотами - (*) (для x_i).

Статистическим распределением выборки называют таблицу, где указан пере-чень вариант и соответствующих им частот или относительных частот.

xi	x1	x2	…	xk
pi*	p1*	p2*	…	pk*

В этом случае говорят, что составлен дискретный ряд распределения. Такой ряд со­ставляется по результатам наблюдений над дискретной случайной величиной.

В теории вероятностей под распределением дискретной случайной величины пони­мают соответствие между возможными значениями случайной величины и их ве-роятностями, а в математической статистике – соответствие между наблюдаемыми ва-риантами и их частотами или относительными частотами.

Если у нас есть результат наблюдений над непрерывной случайной величиной, то то­гда статистическое распределение выборки задаётся интервальным рядом распределе-ния. В этом случае весь диапазон наблюдаемых значений случайной величины разделим на интервалы и подсчитаем количество значений m_i, приходящихся на каждый i -й интервал.

- относительная частота, приходящаяся на i -й интервал, где n – объём вы­борки, .

I	(x1, x2)	(x2, x3)	…	(xk, xk+1)
mi pi*	m1 p1*	m2 p2*	… …	mk pk*

Эту таблицу называют интервальным рядом распределения.

 

§5. Эмпирическая функция распределения.

 

В теории вероятностей F (x) мы называем теоретической функцией распределения. В математической статистике F *(x) – эмпирическая функция распределения.

Пусть изучается распределение некоторого количественного признака X – слу-чай­ная величина, и в результате n независимых наблюдений получена конкретная вы-борка x₁, x₂, …, x_n.

Обозначим: n_x – это число вариант в конкретной выборке, меньшее x.

Пример.

2,4,6,7,8

x =4,5; n_x =2

Тогда определим функцию - это эмпирическая функция распределе-ния выборки, определяющая для каждого значения x относительную частоту события X < x.

Можно показать, что при больших n эмпирическая функция распределения близка к теоретической функции распределения.

Теорема.

(без доказательства).

Свойства функции F *(x) (функция F *(x) имеет те же свойства, что и F (x)):

1. .

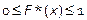2. F *(x) – неубывающая.

3. Если x₁ – наименьшая варианта, F *(x)=0, x ≤ x₁. Если x_k – наибольшая варианта, F *(x)=1, x > x_k.

Пример.

Построить эмпирическую функцию распределения по данной выборке:

xi
ni

Дискретный ряд, объём выборки n =6+16+18+20=60.

; ; ; .

 

Скачки на графике F_x* равны относительным частотам.

 

§6. Полигон и гистограмма.

 

Статистическое распределение выборки графически отображается в виде полиго-на и гистограммы.

Дискретный ряд распределения отображается в виде полигона.

(x_i, n_i) – полигон частот

 

Можно построить полигон относитель-ных частот.

 

Интервальный ряд распределе-ния отображается графически при по-мощи гисто­граммы. По оси абсцисс откладываются интервалы, и на каждом из них строится прямоуголь­ник, площадь которого равна относительной частоте данного интервала, а высота прямоугольника равна относительной частоте интервала, поделённой на его длину, т.е. .

, площадь под гистограммой - .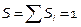

Величину 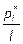называют плотностью относительной частоты, она является оцен-кой плотности вероятности f (x) генеральной совокупности.

Пример.

Выборка задана интервальным рядом распределения. Построить гистограмму выбо­рочной оценки плотности вероятности.

Ii	(-4,-3)	(-3,-2)	(-2,-1)	(-1,0)	(0,1)	(1,2)	(2,3)	(3,4)
mi
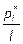
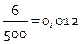
		0,05	0,144	0,266	0,24	0,176	0,092	0,02

; n =500

Высота столбика точно отображает количество значений выборочных данных, которые принадлежат соответствующему интервалу, и даёт наглядное представление о местах с повышенной концентрацией данных. Используя эти данные, при помощи интервального ряда распределения можно приближённо построить эмпирическую функцию распределения.

F *(-4) =0; F *(-3) =0,012;

F *(-2) =0,062; F *(-1) =0,206;

F *(0) =0,472;

F *(1) =0,712; F *(2) =0,888;

F *(3) =0,980; F *(4) =1.

 

§7. Статистические оценки.

 

Рассмотрим задачу оценки закона распределения генеральной случайной величины на основе выборочных данных. Пусть вид закона распределения генеральной случайной величины известен, но неизвестны его параметры, например, математическое ожидание и дисперсия.

Требуется на основе выборочных данных найти приближённые значения этих параметров, т.е. найти статистические оценки этих параметров.

Существует два подхода к оценке неизвестных параметров распределения по наблюдениям:

1) точечный – указывает лишь точку, около которой находится оцениваемый параметр

2) интервальный – находят интервал, который с заданной вероятностью накрывает числовое значение параметра

θ * - оценка неизвестного параметра θ.

Пусть в результате n независимых наблюдений над генеральной случайной величиной получена конкретная выборка x₁, x₂, …, x_n. По этой выборке мы можем рассчитать оценку θ *.

Если бы мы имели k конкретных выборок того же объёма n, то для каждой такой выборки мы смогли бы рассчитать оценки параметра θ: - различные числа, т.е. мы бы получили разные оценки.

Таким образом, оценку θ * можно рассматривать как случайную величину, а - это её конкретные реализации.

Понимая под случайной выборкой весь мыслимый набор конкретных выборок, определим оценку θ * как функцию от случайной выборки, где X₁, X₂, …, X_k - независимые, одинаково распределённые случайные величины, и распределение – такое же, как распределение генеральной случайной величины (т.к. все они имеют одно и то же математическое ожидание a и дисперсию σ²): .

Как определить качество оценки? Качество определяют, проверяя, выполняются ли следующие три свойства:

1) состоятельность оценки – оценка θ * называется состоятельной, если она сходится по вероятности к истинному значению оценки θ *, т.е.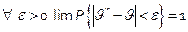

Это свойство является обязательным, несостоятельные оценки не рассматриваются.

2) несмещённость оценки – оценка называется несмещённой, если M (θ *) равно её истинному значению θ

Это свойство является желательным, но не обязательным. Если полученная нами оценка является смещённой, то её можно поправить так, чтобы она стала несмещённой.

3) эффективность оценки – оценка называется эффективной, если она - самая точная в данном классе оценок θ *, т.е. имеет минимальную дисперсию

 

Выборочная средняя.

Выборочной средней называется среднее арифметическое значений выборки.

Если все варианты выборки различны, то: .

Если варианты имеют частоты: , 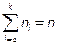- объём выборки.

В ряде случаев все выборочные значения разбиваются на отдельные группы, и в каждой группе находится её среднее значение; среднее значение для группы - групповая средняя . Зная групповые средние, находят общую среднюю для всей выборки и обозначают .

Пример.

Найти общую среднюю на основе выборки:

Группа
Значение варианты
Частота
Объём

Требуется найти групповые средние и общую среднюю.

;

.

Ответ: .

Выборочную среднюю используют в качестве оценки для математического ожидания.

Пусть x₁, x₂, …, x_n – конкретная выборка; X₁, X₂, …, X_n – случайная выборка (все эти случайные величины имеют одно и то же математическое ожидание a и дисперсию σ²).

Для случайной выборки: .

1. Согласно закону больших чисел 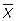- среднее арифметическое независимых, одинаково распределённых случайных величин, имеющих дисперсию σ ², сходится по вероятности к их математическому ожиданию a. Это означает, что - оценка состоятельная.

2. Несмещённость оценки проверим непосредственно. , т.е. оценка является несмещённой.

3. Свойство эффективности. Если распределение генеральной случайной величины – нормальное, то можно доказать, что оценка является эффективной.

 

Выборочная дисперсия.

Выборочная дисперсия является характеристикой рассеивания выборочных значений относительно выборочной средней.

Выборочной дисперсией называется (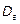) среднее арифметическое квадратов отклонений вариант от выборочной средней.

Если все варианты различны:

Если варианты сгруппированы по частотам:

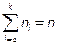- объём выборки

- выборочное среднее квадратическое отклонение (стандартная ошибка).

Для случайной выборки выборочная дисперсия имеет вид: .

Проверим эту оценку на несмещённость:

Рассмотрим каждое слагаемое суммы:

1)

2)

3)

Получим

Оценка имеет систематическое смещение . Это смещение сходит на «нет» при , т.е. оценка асимптотически не смещена.

Поправим так, чтобы она стала несмещённой: - исправленная выборочная дисперсия.

Можно показать, что оценка также является состоятельной.

Теорема.

Выборочная дисперсия равна разности среднего арифметического квадратов значений выборки и квадрата выборочной средней: .

Доказательство.

Пусть выборочные значения (варианты) имеют частоту, тогда

Пример.

Из генеральной совокупности извлечена выборка:

xi	-8	-2
ni
	-6,96	-0,96	2,04	6,04

 

n =50

 

 

Требуется найти выборочную и исправленную дисперсии.

; ;

Ответ: , .

 

Оценка вероятности.

Пусть в генеральной совокупности проводится испытание Бернулли и вероятность успеха p в одном испытании неизвестна.

Оценкой для параметра p является относительная частота , где X – суммарное число успехов за n испытаний, n – объём выборки, p * - конкретное значение относительной частоты.

Если n фиксировано, то p * является таким же, как и распределение суммарного числа успехов, т.е. биномиальным.

Математическое ожидание и среднее квадратическое отклонение биномиального распределения соответственно равны:

; , тогда

оценка является несмещённой.

, где p – вероятность успеха, q =1- p – вероятность неудачи одного испытания Бернулли.

Когда n возрастает, биномиальное распределение стремится к нормальному.

Распределение относительной частоты p * можно приближённо считать нормальным распределением со средним значением p и средним квадратическим отклонением , если и .

Пример.

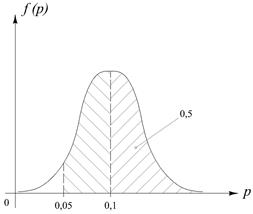
Среди определённой категории людей 10% предпочитают отдыхать на даче. Случайно выбраны 100 человек из этой категории людей. Какова вероятность того, что не менее 5% из них проведут отпуск на даче?

Решение.

Требуется найти вероятность того, что . По условию p =0,1; объём выборки n =100. Т.к. , , то распределение p * можно приближённо считать нормальным с ; . Искомая вероятность равна площади под графиком нормального распределения, лежащей правее вертикали x =0,05.

 

§8. Эмпирические моменты распределения случайных величин.

 

Эмпирическим моментом порядка k называется среднее арифметическое значений k -х степеней разностей (x_i - C).

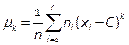; - объём выборки.

C – произвольное постоянное число (ложный нуль).

Различают начальные и центральные эмпирические моменты.

Начальные эмпирические моменты, когда C=0: ; k=1: - начальный эмпирический момент 1-го порядка (выборочная средняя).

Центральные эмпирические моменты, когда 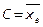: ; k=2: - выборочная дисперсия.

 

§9. Методы точечного оценивания параметров распределения.

 

1. Метод моментов.

Пусть вид закона распределения генеральной случайной величины f(x) известен, например, из соображений, связанных с существом задачи. В выражение плотности f(x) входит несколько параметров. Требуется найти точечные оценки этих параметров.

Метод моментов состоит в том, что точечные оценки неизвестных параметров распределения выбирают так, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим характеристикам (моментам) эмпирического распределения.

Пример.

Рассмотрим показательное распределение .

Это распределение зависит только от одного параметра λ. Найдём точечную оценку этого параметра.

Поскольку нам нужно найти оценку только одного параметра распределения, то достаточно составить только одно уравнение.

(1)

Приравниваем 1-й теоретический момент и 1-й начальный эмпирический момент,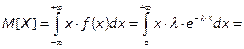

Проинтегрируем это выражение по частям по формуле .

.

Подставим в (1): ; .

Если плотность распределения f(x) зависит от двух параметров, то для отыскания их оценок составляют два уравнения. К уравнению (1) добавляют уравнение, в котором приравнивается 2-й центральный момент теоретического распределения, т.е. генеральная дисперсия и 2-й центральный момент эмпирического распределения, т.е. выборочная дисперсия D_в или исправленная выборочная дисперсия S².

Пример.

Пусть известно, что статистическое распределение, заданное интервальным рядом (см. табл. §6), подчинено нормальному закону распределения: .

Ii	(-4,-3)	(-3,-2)	(-2,-1)	(-1,0)	(0,1)	(1,2)	(2,3)	(3,4)
mi
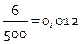
		0,05	0,144	0,266	0,24	0,176	0,092	0,02

; n =500

Найти точечные оценки параметров a (мат. ож.) и σ (ср. квадратическое откл.).

- середина интервала,

Ответ: ; .

2. Метод наибольшего правдоподобия.

В основе метода лежит понятие функции правдоподобия. Пусть X – генеральная случайная величина и x₁, x₂, …, x_n – конкретная выборка из генеральной совокупности. Известен вид распределения, но неизвестны его параметры. Найти оценки неизвестных параметров распределения.

Обозначим 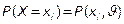, где θ – оцениваемый параметр.

1) X – дискретная случайная величина. Функцией правдоподобия в этом случае называют функцию . При фиксированном θ функция правдоподобия – это вероятность или мера правдоподобия набора x₁, x₂, …, x_n. Чем вероятнее наблюдать выборку x₁, x₂, …, x_n, тем большее значение имеет функция , поэтому за точечную оценку параметра θ принимают такое его значение θ*, при котором функция L имеет максимум. Такую оценку называют оценкой наибольшего правдоподобия. Если L(θ) имеет точку максимума, то и lnL(θ) имеет точку максимума, т.е. их максимумы совпадают, поэтому вместо L(θ) используют lnL(θ) и находят точку максимума, т.к. это технически проще и удобнее.

2) X – непрерывная случайная величина. , и предполагаем, что функция плотности f(x_i,θ) известна.

Пример.

Найдём методом наибольшего правдоподобия оценку параметра λ в распределении Пуассона.

Рассмотрим составной опыт из r независимых опытов. Каждый опыт имеет 2 исхода: успех – p, неудача – (1-p), всего n составных опытов.

, где x_i – число успехов в i -м составном опыте, .

Составим функцию правдоподобия

.

Будем рассматривать эту функцию правдоподобия как функцию одного параметра λ, и найдём максимум функции .

1. Находим критическую точку: ,

; при получим , или .

2. Проверяем достаточное условие существования экстремума:

.

Ответ: .

 

§10. Критические границы.

 

Это понятие для непрерывных случайных величин широко используется в математической статистике при построении доверительных интервалов и критериев проверки гипотез. Различают левосторонние, правосторонние и двусторонние критические границы.

Левосторонней критической границей, или квантилью, отвечающей вероятности α, называется такая граница K_α, левее которой вероятность равна α.

, т.о. квантиль определяется критерием: (1).

Правосторонней критической границей, отвечающей вероятности α, называется такая граница B_α, правее которой вероятность равна α.

По определению: . Правосторонняя граница является решением уравнения (2).

Установим связь между правосторонней и левосторонней границами:

Двусторонними критическими границами, отвечающими вероятности α, называются такие границы и , внутрь которых случайная величина попадает с вероятностью (1-α), а вне интервала, определяемого этими границами - с вероятностью α, причём .

Таким образом, двусторонние критические границы являются решением уравнений:

; .

Между односторонними и двусторонними границами существующие соотношения определяются равенствами:

; .

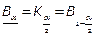Для стандартного нормального распределения двусторонние критические границы симметричны и обозначаются , т.е. , .

В дальнейшем мы убедимся в том, что .

 

§11. Основные законы распределения статистических оценок.

 

В качестве законов распределения статистических оценок используют следующие распределения.

 

Распределение χ².

Пусть X₀, X₁, …, X_n – независимые, стандартные, нормальные случайные величины (a =0, σ =1).

Распределение суммы квадратов этих случайных величин называется распределением χ² с n степенями свободы:

.

Число степеней свободы равно разности общего числа неизвестных и связей между этими неизвестными.

Изобразим графики функции плотности для разных степеней свободы:

Значение χ² распределения находится по таблице. При построении доверительных интервалов и проверке гипотез используются двусторонние критические границы χ². Поскольку двусторонние критические границы можно определить по односторонним, то обычно в таблице приводятся только правосторонние критические границы для каждого значения степеней свободы.

 

 

Распределение Стьюдента.

Рассмотрим случайную величину , где X₀ – стандартное нормальное распределение, причём случайная величина X₀ и - независимые. Такое распределение называется распределением Стьюдента с n степенями свободы. При распределение Стьюдента стремится к нормальному.

График плотности распределения Стьюдента является симметричным, но более плоским, чем график плотности нормального распределения и выше графика нормального распределения по краям. Двусторонние критические границы распределения Стьюдента шире соответствующих двусторонних границ нормального распределения: t_α>U_α. Обычно в таблице приводятся правосторонние двусторонние границы t_α(n) для разных значений степеней свободы.

 

Распределение Фишера.

χ²(m), χ²(n) – независимые случайные величины, имеющие распределение χ² с m и n степенями свободы соответственно.

- распределение Фишера с m и n степенями свободы.

 

§12. Интервальные оценки параметров нормального распределения.

 

Вычисленная на основе выборки точечная оценка θ* является лишь приближением к неизвестному значению параметра θ даже в том случае, когда оценка является состоятельной, несмещённой и эффективной.

Пусть γ=1-α – заданная, близкая к единице вероятность.

Если , (1)

то интервал (θ*-δ, θ*+δ) называется интервальной оценкой параметра θ или доверительным интервалом.

γ =0,99; γ =0,95; … γ =0,9 и т.д.

Точечная оценка θ* - случайная величина; число δ – ошибка оценки, случайная величина, которая зависит выборки и от γ (надёжность оценки или доверительная вероятность). Поэтому доверительный интервал также случайный.

Выражение (1) понимают так: интервал (θ*-δ, θ*+δ) накроет истинное значение параметра θ с вероятностью γ.

 

Схема построения интервальной оценки при конечном объёме выборки n.

1. Подбирается функция ψ(θ*,θ), которая удовлетворяет следующим двум условиям:

1) закон распределения ψ(θ*,θ) известен, но не зависит от θ

2) функция ψ непрерывна и строго монотонна по параметру θ

2. Задав доверительный интервал γ=1-α, находят двусторонние критические границы и , отвечающие вероятности γ=1-α. Тогда с вероятностью γ выполняется неравенство (2) Решив это неравенство (2) относительно θ, находят границы доверительного интервала: θ*-δ – нижняя граница доверительного интервала, θ*+δ – верхняя граница доверительного интервала Функцию ψ(θ*,θ) называют статистикой. Если плотность распределения ψ(θ*,θ) симметрична относительно оси OY, то доверительный интервал симметричен относительно θ*.

 

Общая схема построения доверительного интервала.

1. Из генеральной совокупности с известным распределением f(x,θ) случайной величины X извлекается выборка объёма n, и по ней находится точечная оценка θ* параметра θ.

2. Выбирается статистика ψ(θ*,θ), закон распределения которой известен.

3. Задаётся уровень значимости α (вероятность; 1-α=γ – надёжность оценки).

4. Находят двусторонние критические границы распределения ψ(θ*,θ), тогда