§1. Понятие о многомерных случайных величинах.
Случайный опыт характеризуется, как правило, не одной, а несколькими случайными величинами. Например, состояние газа в сосуде определяется давлением и температурой. При изготовлении труб контролируется внутренний диаметр и внешний диаметр. Многие экономические показатели являются многомерными случайными величинами, например, уровень жизни населения:
- ВНП на душу населения
- распределение доходов
- продолжительной жизни
- экологические факторы
- издержки предприятий: постоянные и переменные
Определение: говорят, что задана многомерная случайная величина или n-мерный случайный вектор X =(X1, X2,…, Xn). Если на одном и том же вероятностном пространстве (E, K, P) задано n случайных величин:
X1 (e), X2 (e), …, Xn (e)
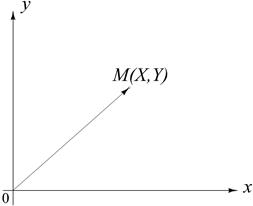
Мы будем рассматривать двумерную случайную величину (X, Y). Геометрически будем её использовать как случайную точку M (X, Y) на плоскости или как случайный вектор 
на плоскости.
Как и в одномерном случае, закон распределения двумерной случайной величины определяется функцией распределения 
, которая является числовой функцией двух переменных и как вероятность принимает значения на отрезке [0,1].
Геометрически – это вероятность того, что случайная точка попадает в бесконечный квадрат с вершиной в точке (x, y), расположенный левее и ниже этой вершины.
Свойства F ( x, y ).
1. F (x, y) – неубывающая:
F (x2, y)≥ F (x1, y), если x2 > x1
F (x, y2)≥ F (x, y1), если y2 > y1
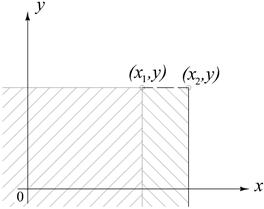
Вероятность попадания в квадрант с вершиной (x2, y) не может уменьшиться.
2. F (+∞,+∞)≥1. Квадрант с вершиной (x, y) при 
, 
обращается во всю плоскость XoY, попадание в которую случайной точки – есть достоверное событие.
3. F (-∞, y)= F (x,-∞)=0.
Частные законы распределения. Независимость случайных величин.
Дана двумерная случайная величина (X, Y) и F (x, y) – функция распределения.
F(x,y) – функция распределения.
F(x,y) – вероятность того, что 
.
, 
.
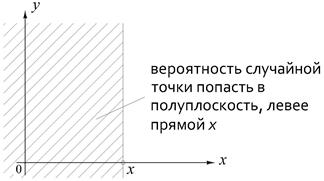
Говорят, что функция F(x,y) задаёт совместный закон распределения случайных величин X и Y, а функции F1(x) и F2(y) – частные законы распределения составляющих X и Y. Зная совместный закон, можно определить частные распределения.
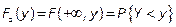
Определение. Случайные величины X и Y называются независимыми, если для любых действительных x и y выполняется равенство 
. Для случая независимого распределения по частным распределениям мы можем выставить совместный закон распределения.
§2. Дискретная двумерная случайная величина.
Случайная величина (X, Y) называется дискретной, если дискретны обе её составляющие.
Обозначим xi – возможные значения случайной величины X, i =1,2,…, n; обозначим yj – возможные значения случайной величины Y, j=1,2,…, m. Тогда возможные значения двумерной случайной величины – это пары вида 
. Обозначим 
, 
, Pij ≥0.
Закон распределения дискретной двумерной случайной величины задаётся с помощью таблицы, которая имеет 2 входа:
| X Y | x1 | x2 | … | xi | … | xn |
| y1 | P11 | P21 | … | Pi1 | Pn1 | |
| y2 | P12 | P22 | … | Pi2 | … | Pn2 |
| … | ||||||
| yj | P1j | P2j | … | Pij | … | Pnj |
| … | ||||||
| ym | P1m | P2m | … | Pim | … | Pnm |
Вероятности Pij задают совместный закон распределения.
Эти вероятности задают частные распределения. Выясним, как выражаются частные законы распределения через совместные.
X = xi, т.к. события 
, 
, …, 
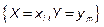несовместны, то по аксиоме сложения вероятностей 
.
Аналогично, 
.
Дискретные случайные величины X и Y называются независимыми 
.
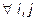Мы знаем, что если события A и B являются зависимыми, то условная вероятность события B отличается от его безусловной вероятности: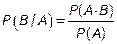 
.
Для характеристики зависимости между составляющими двумерной случайной величины вводят понятие условного распределения. Условным распределением составляющей X при Y = yj называют 
, 
, …, 
. Все эти вероятности вычисляются в предположении, что событие Y = yj уже наступило.
Зная совместный закон распределения двумерной дискретной случайной величины, можно определить условные законы распределения составляющих:
, 
.
Пример.
Дан закон распределения двумерной случайной величины. Выяснить, являются ли X и Y независимыми случайными величинами.
| X Y | |||
| 
|
| |
|
| 
|
| |
|
|
|
|
, 
, 
, 
, 
, 
, 
, , 
, 
, 
, 
, 
, 
, , 
, 
, 
, 
, , 
, 
, 
, , 
, , , 
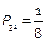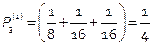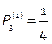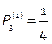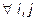
дискретные случайные величины X и Y – независимы.
Ответ: случайные величины X и Y – независимы.
§3. Непрерывная двумерная случайная величина.
Случайная величина (X, Y) называется непрерывной, если непрерывны обе её составляющие. Пусть функция распределения F (x, y) всюду непрерывна и имеет всюду непрерывную частную производную 
.
Определение. Функция 
называется плотностью распределения непрерывной двумерной случайной величины (X, Y). Графиком этой функции f (x, y) является некоторая поверхность, которую называют поверхностью распределения.
Вероятность попадания случайной точки в прямоугольник со сторонами, параллельными координатным осям.
(вероятность попасть в область)
(*) 
Свойства функции f ( x, y ).
1. Рассмотрим на плоскости прямоугольник R со сторонами Δ x и Δ y, примыкающий к точке (x1, y1) и со сторонами, параллельными осям OX и OY.
Используя (*), подсчитаем 
Получим 
- отношение вероятности попадания случайной точки в прямоугольник к площади этого прямоугольника.
Перейдём в этом равенстве к пределу 
.
Из этого равенства следует, что с точностью до бесконечно малых более высокого
порядка, чем Δ x и Δ y 
} 
.
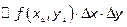Рассмотрим на плоскости произвольную область D, и разложим её на n ячеек прямыми, параллельными оси OY и оси OX на расстоянии Δ x и Δ y друг от друга соответственно.
Т.к. события, состоящие в попадании случайной точки в каждую из ячеек ei, несовместны, то мы можем использовать аксиому 3:
- интегральная сумма для f (x, y) по области D.
Перейдём в этом равенстве к пределу при 
и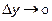 
:
Мы получили возможность выразить функцию F через функцию f: 
.
2. 
3. 
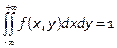
Пример.
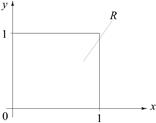Задана плотность распределения 
. Найти F (x, y) и вероятность попадания случайной точки в прямоугольник
Решение.
Ответ: .
Пусть известно f (x, y)
f1 (x), f2 (y) -?
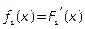
Теорема.
Непрерывные случайные величины X и Y независимы тогда и только тогда, когда 
: X и Y – независимы .
Доказательство.
Известно, что X, Y – независимые случайные величины. Дифференцируем это равенство сначала по x, затем по y.
Известно, что
Дважды интегрируем: по x, затем по y
,
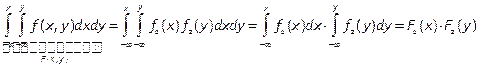т.е. , и X и Y – независимы.
Пример.
Задана функция плотности для двумерной случайной величины
Зависимы ли эти случайные величины?
Решение.
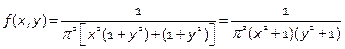
, т.е. X и Y – независимые случайные величины.
Определение. Условной плотностью распределения составляющей X при заданном значении другой составляющей Y = y называется отношение 
.
Аналогично 
.
; 
.
Мы можем найти закон распределения двумерной случайной величины (X, Y), если известен закон распределения одной из составляющих и условный закон распределения другой составляющей.
§4. Числовые характеристики двумерной случайной величины. Ковариация случайных величин X и Y. Коэффициент корреляции.
Для двумерной случайной величины (X, Y) важнейшими числовыми характеристиками являются математические ожидания M (X) и M (Y) и дисперсии D (X) и D (Y).
Совокупность M (X) и M (Y) является характеристикой положения случайной точки (X, Y) – это средняя точка, около которой происходит рассеяние точек (X, Y). Дисперсии D (X) и D (Y) характеризуют рассеяние случайных точек вдоль оси OX и OY. Важнейшей характеристикой условного распределения является условное математическое ожидание.
Условным математическим ожиданием дискретной случайной величины Y при X = x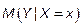 
называют сумму произведений возможных значений случайной величины Y на их условные вероятности: 
.
Для непрерывной случайной величины: 
.
Аналогично и для 
.
Пример.
Найти условное математическое ожидание случайной величины Y на основе заданной таблицы распределения двумерной случайной величины. 
-?
| X Y | ||
| 0,25 | 0,10 | |
| 0,15 | 0,05 | |
| 0,32 | 0,13 |
;
; 
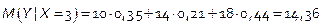
Ответ: 14,36.
Для случайных величин X и Y характеристикой зависимости является математическое ожидание произведения центрированных случайных величин:
- ковариация случайных величин X и Y.
Приведём формулы ковариации для непрерывных и случайных величин.
Дискретная случайная величина: 
- двойная сумма (суммируется по одной величине, затем по другой).
Непрерывная случайная величина: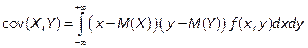 
.
для непрерывной и дискретной случайных величин.
Теорема.
Если случайные величины X и Y независимы, то их ковариация равна нулю.
X, Y – независимы 
Доказательство.
X, Y – независимы
Если 
, то это является признаком наличия зависимости между X и Y.
зависит от размерностей случайных величин X и Y, и при различных единицах измерения этих случайных величин мы будем получать разные значения для . Это затрудняет сравнение для различных двумерных случайных величин, поэтому вводится безразмерная характеристика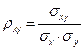 
- коэффициент корреляции случайных величин X и Y.
Две случайные величины X и Y называются коррелированными, если 
. Если 
, то X и Y – некоррелированные. Если X, Y – коррелированные, то они и зависимы.
Если X, Y – независимые, то они некоррелированные.
Если X, Y – некоррелированные, то не следует независимость.
Все значения коэффициента корреляции принадлежат 
, причём, если случайные величины:
1. X и Y связаны линейной зависимостью (Y =α+β x), 
.
2. X, Y – независимые, то .
3. Для всех остальных случаев 
.