Задачи на построение
Задача на построение это задача, в которой требуется построить геометрический объект, пользуясь только двумя инструментами: циркулем и линейкой (односторонней и без делений).
Решение таких задач состоит не в том, чтобы проделать «руками» соответствующие построения и описать их, а в том, чтобы найти алгоритм решения, то есть, описать решение задачи в виде последовательности уже известных стандартных построений.
В этом смысле решение задач на построение хорошо иллюстрирует один из основных принципов решения любых математических задач: решить задачу это значит свести ее к какой-либо задаче, уже решенной ранее!
Какие построения циркулем и линейкой считать стандартными?
Это вопрос предварительной договоренности. Договоримся, к стандартным построениям отнести следующие:
1) построение прямой, проходящей через две заданные точки;
2) построение окружности с данным центром и данным радиусом;
3) построение отрезка, равного данному;
4) построение угла, равного данному;
5) построение середины отрезка (серединного перпендикуляра к отрезку);
6) построение биссектрисы угла;
7) построение перпендикуляра к прямой, проходящего через заданную точку (два случая).
На основе этих стандартных построений легко осуществляется построение треугольниковпо трем основным элементам: 1) двум сторонам и углу; 2) стороне и двум углам; 3) трем сторонам. При этом очень важно понимать, что все линейные элементы в условиях задач заданы в виде отрезков (а не их длин), а все угловые – в виде углов (а не чисел, выражающих их величину)!
Далее, к тем же типовым построениям сводятся также построения равнобедренных и прямоугольных треугольников по их основным элементам, а также построение прямой, параллельной данной и проходящей через заданную точку (как это сделать?).
Таким образом, можно провести некоторую аналогию между решением задач на построение и строительством домов: стандартные построения – это «кирпичи», задачи на построение различных видов треугольников по их основным элементам – «блоки».
Теперь, пользуясь этими «блоками», можно приступить к решению задач, причем решенная задача становится готовой «панелью», которую можно целиком использовать при решении других задач. При этом, для того, чтобы научится решать задачи на построение (впрочем, как и другие геометрические задачи) очень важно осознавать, что решать их надо с конца, то есть не пытаться строить все, что умеешь, наугад, а представить себе, что искомый объект уже построен и, исходя из этого, восстановить цепочку возможных построений в виде крупных «блоков» или «панелей».
Выделим два основных метода решений задач на построение:
· метод вспомогательного треугольника
· метод геометрических мест точек.
|
1) Суть метода вспомогательного треугольника – свести решаемую задачу к уже известной задаче на построение треугольника по основным элементам или к уже решенной задаче на построение треугольника по каким-то другим элементам.
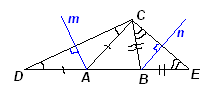
Пример 1. Объясните, как построить треугольник по двум его углам и периметру.
| Рис. 1 |
Решение. Пусть искомый треугольник АВС с данным периметром P и углами a и b при вершинах А и В соответственно – построен. «Развернем» его, то есть на прямой АВ отложим отрезок AD, равный АС, и отрезок ВЕ, равный ВС. Полученные толчки D и Е соединим с точкой С (см. рис. 1).
Заметим, что треугольник ACD – равнобедренный, угол САВ – внешний для этого треугольника, поэтому Ð СDА = Ð DCА = 
. Аналогично, Ð СЕВ = Ð ECB = 
.
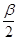Таким образом, задача сводится к построению вспомогательного треугольника СDЕ по стороне и двум прилежащим к ней углам (DE = P, Ð СDE = , Ð СЕD = 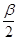). Для того, чтобы теперь получить вершины А и В искомого треугольника, достаточно, например, провести серединные перпендикуляры m и n к отрезкам CD и СЕ соответственно.
Отметим, что в подавляющем большинстве случаев, когда задана сумма (или разность) каких-либо отрезков, полезно сделать дополнительное построение, в результате которого заданный отрезок появляется на чертеже. Такой метод иногда называют «спрямлением» (и он применяется не только в задачах на построение).
2) Метод геометрических мест основан на том, что часть объектов, получаемых при стандартных построениях циркулем и линейкой, являются одновременно ГМТ, обладающих определенными свойствами. Например, окружность является геометрическим местом точек, удаленных от заданной точки на фиксированное расстояние; серединный перпендикуляр к отрезку – ГМТ, равноудаленных от концов отрезка; биссектриса угла – ГМТ, лежащих внутри угла и равноудаленных от его сторон и т. д. Помимо этого, некоторые ГМТ несложно построить, используя простейшие построения, метод вспомогательных треугольников и уже построенные ГМТ.
Суть метода ГМТ состоит в следующем: если некоторая точка X удовлетворяет двум условиям, то строятся ГМТ, удовлетворяющие каждому из этих условий, и тогда точка X принадлежит их пересечению.
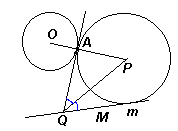
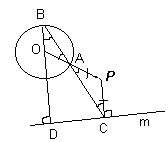
Пример 2. Объясните, как построить окружность, касающуюся данной прямой m и касающуюся данной окружности в данной точке А внешним образом.
|
| Рис. 2а |
Решение. Пусть даны прямая m и окружность с центром О, на которой отмечена точка А. Пусть искомая окружность построена, Р – ее центр (см. рис. 2 а, б). Так как искомая окружность проходит через фиксированную точку А, то для построения этой окружности достаточно построить ее центр Р. Так как окружности касаются в точке А внешним образом, то точки О, А и Р лежат на одной прямой (А – между О и Р).
|
| Рис. 2б |
Первый способ. Если через точку А провести также общую касательную AQ к этим окружностям (Q – точка ее пересечения с данной прямой m), то луч QР будет являться биссектрисой угла АQM (см. рис. 2а).
Таким образом, решение задачи сводится к построению луча ОА, касательной QА к данной окружности и биссектрисы QР угла АQM. Р – точка пересечения лучей ОА и QР.
Второй способ. Рассмотрим перпендикуляры OD и РC, опущенные из центров данной и искомой окружности на прямую m (см. рис. 2б). Пусть В – одна из точек пересечения OD и данной окружности, тогда, так как BD || PC, то Ð OAB = Ð DBC = Ð PCB = Ð PAC, значит, углы ОАВ и РАС – вертикальные, то есть точка А лежит на прямой ВС. Следовательно, искомая точка P лежит на перпендикуляре, проведенном к данной прямой из точки С, которая является пересечением прямых m и АВ.
Отметим, что если касательная QA параллельна прямой m (первый способ решения) или, что равносильно, точка А лежит на отрезке BD (второй способ решения), то решением задачи является окружность с диаметром AD.
Отметим также, что решая задачу вторым способом и выбрав вместо точки В ей диаметрально противоположную, получим не внешнее, а внутреннее касание окружностей.