Простые алгоритмы сортировки массива

 

Как было отмечено в разделе 1, в алгоритмах сортировки массива мы будем пользоваться только одной “вспомогательной” переменной типа Элемент. Эта переменная используется для обмена двух элементов мас­сива. Поскольку обмен некоторых двух элементов массива многократно используется во всех алгоритмах сортировки, оформим этот небольшой подалгоритм в виде процедуры:

procedure Обмен (I,J: word);

var Эл: Элемент;

begin

Эл:=Массив[J];

Массив^]:=Массив[!];

Массив[I]:=Эл;

end;

Иногда будем пользоваться модификацией этого алгоритма: менять элементы только тогда, когда ключ (Ключ) первого параметра больше ключа второго. В программах будет использоваться результат рабо­ты этого алгоритма – т.е. действительно ли мы поменяли элементы ме­стами, – поэтому оформим этот подалгоритм в виде такой логической функции:

function Упорядочили (I, J: word): boolean;

begin

if Массив[I].Ключ>Массив[J].Ключ

then begin Обмен(I,J); Упорядочили:=true; end

else Упорядочили:=false;

end;

Удобно выделить в качестве подалгоритма и циклический сдвиг нескольких элементов массива (ср. с процедурой Обмен):

procedure Сдвиг (I,J: word);

{Циклический сдвиг элементов:

либо I -> I+1 -> I+2 ->...-> J-1 -> J (при I<J),

либо I -> I-1 -> I-2 ->...-> J+1 -> J (при I>J).

}

var Эл: Элемент;

K: word;

begin

Эл:=Массив[J];

if J>I

then for K:=J downto I+1 do Массив[K]:=МассивК-1]

else for K:=J to I-1 do Массив[K]:=МассивК+1];

Массив[I]:=Эл;

end;

Рассмотренную ранее процедуру обмена двух элементов массива можно было бы также написать как частный случай алгоритма Сдвиг, - однако это, по-видимому, нерационально. Отметим также, что мы только один раз - а именно, при написании процедуры Сдвиг - выясняем, какой из наших двух элементов (I-й или J-й) имеет мень ши й номер. В даль­нейшем же, т.е. при применении процедуры Сдвиг, мы будем заботиться только о том, чтобы направление от первого из номеров-параметров ко второму было именно направлением сдвига.

Ниже, при печати текстов программ сортировки, мы не будем специ­ально отмечать то, что описания приведённых трёх алгоритмов обмена и сдвига - Обмен, Упорядочили и Сдвиг - всегда опущены. Отметим, что если несколько различных процедур сортировки собраны в единый мо­дуль, то три упомянутых подалгоритма должны оформляться “наравне” с остальными - т.е. быть доступными для всех других процедур^[8].

 

4.1 Метод прямого включения

Неформально алгоритм этого метода (итерационный процесс) описыва­ется следующим образом: в процессе работы алгоритма все элементы де­лятся на уже отсортированную часть, находящуюся в начале массива и ещё не отсортированную, находящуюся в конце. База итерационно­го процесса: можно считать, что в начале работы эта граница находится между первым и вторым элементами (т. к. массив из одного элемента все­гда является отсортированным). Шаг процесса: выбирается первый эле­мент второй части и переносится на необходимое место в первой части; при этом граница между частями массива сдвигается на один элемент.

Продемонстрируем алгоритм на примере. Будем здесь и всюду ниже на рисунках, поясняющих метод, изображать только ключи элементов (т.е. поля Ключ переменных типа Элемент). Кроме этого, предполагаем, что в нарисованных горизонтально массивах первый элемент находится слева, последний – справа, а в нарисованных вертикально – первый элемент является верхним. Изменения массива показаны здесь сверху вниз, граница между частями массива – толстая линия, рассматриваемый элемент выделен шрифтом большего размера, место в первой части, куда происходит включение - стрелкой.

 

Как мы видим, граница между частями массива “уехала” за границу массива - на этом сортировка кончается.

Программа для метода прямого включения несложна, отметим л иш ь использование в ней двух ранее рассмотренных подалгоритмов – дихото­мии (при использовании вместо неё линейного поиска ^[9] эффективность была бы ещё ниже), а также сдвига.

procedure ПрямоеВключение (Граница: word); var I,J: word;

Куда: word;

begin

for I:=2 to Граница do begin

Куда:=Дихотомия(I-1,Массив[I].Ключ);

{дихотомией нашли,

куда переписать рассматриваемый элемент

}

if Куда>0 then Сдвиг(Куда,I);

{ "else" рассматриваемый элемент не надо

переписывать

}

end;

end;

Оценим эффективность «в худшем» метода прямого включения. Ко­личество сравнений дихотомии мы оценивали ранее - эта величина для массива из n элементов имеет порядок logn. Мы применяем дихотомию n -1 раз, причём для i -го применения массив состоит из i элементов, поэтому общее число сравнений есть

Для подсчёта наибольшего возможного числа пересылок заметим, что на

i -м шаге в худшем случае (а именно - когда рассматриваемый элемент пересылается в 1 -ю позицию) будет i+1 пересылка, т.е. их общее число не превышает

Из последнего заключаем, что для метода прямого включения эффективность “в худшем” есть n².

 

4.2 Методы прямого выбора

Общее во всех методах прямого выбора - то, что на каждом шаге алго­ритмов среди непросмотренной части массива выбирается минимальный (или максимальный) элемент и переносится на первое (последнее) воз­можное место.

Первым рассмотрим метод пузырька, названный так из-за аналогии со всплывающим пузырьком газа в воде.^[10] Алгоритм: на i -м шаге среди непросмотренных элементов (их n-i+1) выбирается минимальный, записывается на i -е место массива, при этом промежуточные элементы сдвигаются (всплыл пузырёк):

 

 

При внимательном рассмотрении рисунка (или процедуры сортиров­ки, составленной на основе описанного алгоритма ^[11])

procedure Пузырек (Граница: word);

{==========}

function Минимум (Левый: word): word;

var I,Num,Key: word;

begin

Num:=Левый; Key:=Массив[Левый].Ключ;

{предполагаемый минимум}

for!:=Левый+1 to Граница do

if Массив[I].Ключ then begin

Num:=I; Key:=Массив[I].Ключ;

{новый предполагаемый минимум}

end;

Min:=M;

end;

{==========}

var I: word;

begin

for I:=1 to Граница-1 do Сдвиг^МинимумЦ));

end;

становится непонятным применение подалгоритма Сдвиг: ведь у нас ещё нет никакой информации об относительных значениях элементов с но­мерами от I+1 до Минимум(I). Поэтому подалгоритм Сдвиг можно заме­нить на более быстрый Обмен, при этом процедура сортировки становит­ся такой^[12]:

procedure ПузырекМ (Граница: word);

var I: word;

begin

for I:=1 to Граница-1 do Обмен(I,Минимум(I));

end;

Вот соответствующий этой процедуре рисунок:

Эффективность метода пузырька посчитаем для последнего вариан­та. Немного переформулируем ранее отмеченный факт: перед i-м шагом алгоритма у нас ещё нет никакой информации об относительных зна­чениях элементов с номерами от i до n. Из этого можно сделать такое заключение: на i-м шаге, вообще говоря, нельзя найти минимальный элемент, не сделав n-i сравнений. Таким образом, в худшем случае общее число сравнений пропорционально

При подсчёте общего числа пересылок естественно учитывать не только те из них, которые вызываются подпрограммой Обмен, но и необходимые для работы функции Минимум^[13]. На любом шаге возможны 3 пересыл­ки «первого рода», а максимально возможное число пересылок «второго рода» зависит от номера шага алгоритма: на i-м шаге их число равно 2*(n—i+1). Таким образом, для всего алгоритма максимально воз­можное число пересылок есть

т. е. и для метода пузырька мы получаем такую же оценку эффективности: n².

Далее рассмотрим один из вариантов т. н. шейкерной сортировки, также являющейся развитием метода пузырька^[14]. Сначала отметим сле­дующий факт: во всех рассмотренных ранее алгоритмах возможны си­туации, когда наш массив оказался отсортированным до окончания ра­боты алгоритма. Интуитивно ясно, что многократные проверки такой ситуации (для досрочного окончания работы алгоритмов в случае её обнаружения) приведёт к существенному снижению эффективности. Однако возможны ситуации, когда заранее известно, что входной массив «почти отсортирован» ^[15]. Рассмотрим два примера.

Во-первых, применяя метод пузырька к такому массиву:

33 11 51 64 17 83 90 32

увидим, что три «пузырька» - 11, 17 и 32 - полностью отсортируют массив. Однако массив

90 11 17 32 33 51 64 83,

который тем более хочется назвать «почти отсортированным» - требу­ет для сортировки максимально возможное (для размерности 8) число «пузырьков» 7.

Последний пример подсказывает такой алгоритм: чередовать перенос наверх минимального (из оставшихся) элемента и перенос вниз макси­мального («топорик»?). При таком алгоритме сортировка обоих «почти отсортированных» массивов завершается менее чем за 7 шагов - это, по-видимому, легко понять и без поясняющих рисунков. Процедура по­лучается такая:

procedure Шейкер (Граница: word);

var Вверх: boolean;

Левый,Правый: word;

begin

Вверх:=true;

Левый:=1; Правый:=Граница;

while not ПоПорядку(Левый,Правый) do begin

if Вверх then begin

Сдвиг(Левый,Минимум(Левый,Правый));

inc(Левый);

end

else begin

Сдвиг(Правый,Максимум(Левый,Правый));

dec(Правый);

end;

Вверх:=not Вверх;

end;

end;

Функция ПоПорядку в принципе может быть использована и в других алгоритмах, поэтому опишем её отдельно:

function ПоПорядку (Левый,Правый: word): boolean;

var I: word;

begin

ПоПорядку:=false; {пока}

for I:=Левый to Правый-1 do

if Массив[I].Ключ>Массив[I+1].Ключ then exit;

ПоПорядку:=true;

end;

К написанному необходимы следующие пояснения. Опущенные подал- горитмы Минимум и Максимум - функции, возвращающие номера мини­мального и максимального элементов среди находящихся между их па­раметрами (аналогичная функция была написана нами ранее). Условие

Левый<Правый в цикле while основной процедуры можно не проверять потому, что это делается при работе функции ПоПорядку. Пе­ременная Вверх используется в качестве переключателя «пузырёк/топо­рик», а подалгоритм ПоПорядку применяется только для «внутренних» элементов массива (т.е. тех, которые расположены между двумя отсор­тированными частями - этого достаточно). Ещё раз отметим применение подалгоритма Сдвиг (при применении вместо него подалгоритма Обмен терялся бы смысл всего метода).

Оценку эффективности метода шейкера проводить не будем по следу­ющим причинам. Во-первых, очевидно, что эффективность «в худшем» совпадает с соответствующей величиной метода пузырька, а нам уже из­вестно, что даже улучшенная процедура ПузырекМ имеет эффективность ~ n². Во-вторых, посчитать эффективность «в среднем» для удачных («почти отсортированных») вариантов расположения элементов (где и можно было бы ожидать меньшую величину) вряд ли вообще возможно - мы приме­няли лишь интуитивные размышления об удачных вариантах расположения элементов. В-третьих, в следующем разделе будет написана несколько более эффективная «процедура‑гибрид» методов шейкера и последовательных обменов.

 

 

4.3 Методы последовательных обменов

Рассмотренный нами в предыдущем подразделе алгоритм ПоПорядку на­водит на мысль не только сравнивать порядок расположения соседних элементов массива, но и переупорядочивать их в случае неверного рас­положения. Таким образом, возникает следующий цикл ^[16]:

for I:=1 to Граница-1 do Упорядочили(I,I+1);

(этот цикл можно назвать подалгоритмом). Подалгоритм «уменьшает эн­тропию» массива, поэтому за некоторое число его применений массив станет отсортированным^[17]. Но - чему равно необходимое число приме­нений последнего подалгоритма? Рассматривая начало его работы, мы убеждаемся что после каждого очередного прохода по крайней мере один элемент - максимальный из оставшихся - попадает на своё место, причём на следующих проходах этот элемент сдвигаться уже не будет.

Отсюда получаем следующие два вывода: во-первых, для массива раз­мерности n подалгоритм достаточно применить n-1 раз; во-вторых, его можно изменить, каждый раз заканчивая цикл на элементе с номе­ром на 1 меньше, чем в пре ды дущем случае. Будем называть описанный алгоритм методом последовательных обменов, для него получается сле­дующая процедура сортировки:

procedure Обмены (Граница: word);

var I,K: word;

begin

for K:=1 to Граница-1 do

for I:=1 to Граница-K do Упорядочили(I,I+1);

end;

Заметим, что после очередного прохода на своём месте может ока­заться не только максимальный из оставшихся элементов, но и ещё несколько (сейчас нас интересуют только следующие по «старшинству»). Пример такой ситуации нами уже был рассмотрен: на последнем рисунке после первого прохода на своём месте оказался не только элемент (с клю­чом) 90, но и 83. Это обстоятельство подсказывает такую модификацию алгоритма последовательностных обменов:

procedure ОбменыМ (Граница: word);

var I,М,тахОбмен: word;

begin

maxОбмен:=Граница-1;

while max0бмен>0 do begin

M:=1;

for I:=1 to max0бмен do

if Упорядочили(I,I+1) then M:=I;

maxОбмен:=М-1;

end;

end;

Здесь во время каждого прохода мы запоминаем максимальный из но­меров элементов, обмененных со следующими за ними, получая границу, отделяющую заведомо упорядоченную часть массива (перед очередным проходом эта граница имеет значение max0бмен+1).

Последняя процедура напоминает такой вариант сортировки, часто встречающийся в учебниках и задачниках по информатике:

procedure ОбменыП (Граница: word);

var 1,Проход: word;

Поменяли: boolean;

begin

repeat

Поменяли:=false;

Проход:=1;

for I:=1 to Граница-Проход do begin

Поменяли:=Упорядочили(I,I+1) or Поменяли; inc(Проход);

end;

until not Поменяли;

end;

Вместо Граница-Проход может “для простоты” быть Граница-1, и пере­менная Проход вообще не использоваться. Отметим порядок логических выражений в дизъюнкции – при применении иного порядка процедура перестаёт работать, т.к. при этом не гарантируется просмотр всей оставшейся части масси­ва, и, следовательно, постановка на место максимального элемента.

Несмотря на очевидные преимущества процедуры ОбменыМ по сравне­нию с Обмены и ОбменыП, понятно, что эти преимущества влияют только на эффективность «в среднем», нами не считаемую. Эффективность же «в худшем» у всех трёх модификаций метода последовательных обменов одинакова; это лучше всего видно на примере «инверсного» массива:

90 83 64 51 33 32 17 11

Попытки закончить сортировку раньше времени здесь успеха не прино­сят, причём и число сравнений, и число пересылок пропорциональны

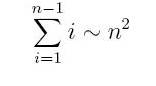
(лу чш е всего последнюю формулу объясняет вариант Обмены).

А теперь вспомним ещё раз про метод шейкера. Оказывается, он име­ет много общего с только что написанной нами процедурой - ведь в функ­ции ПоПорядку мы тоже сравнивали соседние элементы массива. Чтобы результаты этих сравнений не пропадали, попробуем менять элементы в случае неудачного сравнения. А чтобы было совсем похоже на метод шейкера, будем каждый нечётный раз двигаться слева направо (ставя при этом на место максимальный элемент, заодно “уменьшая энтропию” оставшейся части массива), а каждый чётный раз - справа налево (на место ставится минимальный элемент). Получается такая процедура:

procedure ШейкерМ (Граница:word);

var I,М,minОбмен,mахОбмен: word;

Вверх: boolean;

begin

Вверх:=false;

minОбмен:=1; mахОбмен:=Граница-1;

while minОбмен<=mахОбмен do

if Вверх then begin

М:=Граница;

for I:=mахОбмен downto minОбмен do

if Упорядочили(I,I+1) then M:=I;

minОбмен:=М+I;

Вверх:=false;

end

else begin M:=1;

for I:=minОбмен to mахОбмен do

if Упорядочили(I,I+1) then M:=I;

тахОбмен:=М-1;

Вверх:=true;

end;

end;

являющаяся “гибридом” методов шейкера и последовательных обменов. Очевидно, что эффективность процедуры ШейкерМ совпадает с эффектив­ностью каждого из методов последовательных обменов.

Таким образом, можно сделать следующий вывод: эффективность каждого из простых методов сортировки массива ~ n².

 

 

5. Сложные алгоритмы сортировки

массива

5.1 Сортировка с помощью двоичного дерева

В отличие от разобранных выше методов сортировки, описание рассмат­риваемой в данном разделе сортировки с помощью двоичного дерева (поскольку русское название этого метода сортировки не устоялолсь, бу­дем далее называть её английским сокращением – HeapSort) состоит из двух частей – собственно алгоритма и его реализации^[18]. Это связано с тем, что уже сейчас может возникнуть такой вопрос: какое отношение к сортировке массива имеет двоичное дерево? А если читающие данное методическое пособие уже знакомы с динамическими структурами дан­ных, создаваемыми с помощью ссылочных переменных, то вопрос может быть таким: как связаны с массивами двоичные деревья (являющиеся одним из примеров динамических структур данных для представления множеств)? В данном разделе есть ответы на эти вопросы.

Сначала рассмотрим алгоритм сортировки. Будем называть двоич­ными такие деревья, у которых каждая из вершин имеет не более 2 потомков^[19]. Ниже будем рассматривать только т.н. правильные дв оичные деревья – такие, у которых максимально возможное число уровней заполнено полностью, а у не до конца заполненного уровня все имеющие­ся вершины (листья) расположены слева. Очевидно, что для заданного n существует единственное (непомеченное) правильное двоичное дерево, содержащее ровно n вершин.

Представим себе сортируемые элементы массива расположенными в вершинах (как листьях, так и нелистьях) правильного двоичного дере­ва^[20], причём так, что число, расположенное в любой вершине, не меньше, чем расположенное в любой из дочерних. Будем называть такие пра­вильные деревья правильно заполненными. Существует много способов «правильно заполнить» вершины дерева “нашими” 8 элементами ^[21]; два из этих способов см. на приведённых рисунках.

 

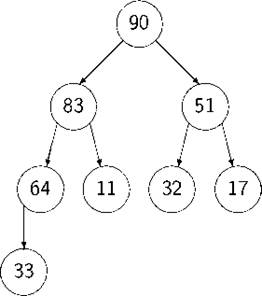
Отметим, что для любого из таких расположений каждая вершина по­мечена максимумом определяемого ею поддерева, и, в частности, корень обязательно помечен максимальным из элементов массива.

Если бы мы умели строить подобное двоичное дерево, то алгоритм сортировки можно было бы записать таким образом:

1. построить дерево;

2. «забрать» корень – максимальный элемент, и перенести его в начало отсортированной части массива;

3. если ещё остались элементы, то перестроить дерево (так, чтобы по­лученное дерево подчинялось ранее сформулированным правилам);

4. перейти на шаг 2.

Мы написали только “заготовку” для алгоритма сортировки HeapSort поскольку ещё остались невыясненными многие вопросы: «как связано двоичное дерево с массивом?»^[22], «как построить дерево?», «как его изме­нять при переносе элемента в отсортированную часть?» и др.

Ответим на главный из этих вопросов - как представить наше дво­ичное дерево в виде массива. Будем предполагать, что вершина дерева соответствует элементу массива, причём корнем является элемент с но­мером 1, а у вершины-элемента с номером i потомками являются эле­менты массива с номерами 2*i и 2*i+1 (если такие существуют). Нарисуем одно из рассмотренных нами правильных деревьев таким об­разом:

 

 

Вопросы всё же остаются: «как построить правильно заполненное дере­во?», «как его изменять?».

Сначала – построим. Будем рассматривать вер ши ны дерева (т.е. элементы массива) с конца, перестраивая при этом поддерево, определяемое рассматриваемой вершиной (корнем), если это поддерево не является правильно заполненным. Отметим, что поддеревья, опре­деляемые листьями общего дерева, заведомо правильно заполненные (т.к. состоят из единственной вершины-корня, не имеющей потомков), поэтому будем перебирать с конца вершины-нелистья. Несложно убе­диться, что независимо от чётности n - числа вершин (правильного) дерева, нелистьями являются вер ши ны с номерами от 1 до [n/2]. Итак, оп иш ем подалгоритм перестройки поддерева. Предполагаем («предпо­ложение индукции»), что все собственные поддеревья рассматриваемого поддерева уже правильно заполнены («базой индукции» при этом яв­ляются листья).

Выберем первую вершину поддерева (корень) в качестве текущей. Рассмотрим прямые потомки текущей вершины (дочерние вершины; их не более 2). Если значение текущей вер ши ны не меньше, чем значение максимальной из дочерних, то процесс обработки поддерева закончен (т.к. по предположению индукции поддеревья дочерних вершин – пра­вильно заполненные). В противном случае поменяем местами значения текущей вершины и максимальной из дочерних, после чего эту верши­ну (куда переместилось значение из текущей) объявим новой текущей. Корректность подалгоритма перестройки доказывается тем, что после описанного обмена только поддерево с корнем в новой текущей вершине может не быть правильно заполненным^[23]. Рассмотрим работу подалгоритма на старом примере. “Просеиваемое” число на рисунках обведено кружком, а стрелками показаны прямые потомки вершины, в которой оно расположено. Каждое применение подалгоритма названо проходом.

 

 

 

 

После приведённого обсуждения процедура Sift сложности не пред­ставляет:

procedure Sift (КореньПоддерева,ГраницаПоддерева: word);

var I,J,J1,J2: word;

begin

I:=КореньПоддерева;

repeat

J:=I;

{вычисляем номера дочерних вершин для J-й}

J1:=2*J; if J1>ГраницаПоддерева then exit;

J2:=J1+1;

if (J2>Lim) or (Массив[J1].Ключ>Массив[J2].Ключ)

then I:=J1

else I:=J2; until not Упорядочили(I,J);

end;

Отметим, что функция Упорядочили используется здесь не совсем обыч­ным способом – для “обратного” обмена, т.к. при этом, в отличие от предыдущих использований, значение первого параметра больше значе­ния второго: I>J. Пока не понятен смысл введения второго параметра (т.е. ГраницаПоддерева – ведь Sift, по-видимому, будет использована как «внутренняя» процедура алгоритма сортировки), – но этот момент прояснится в дальнейшем.

Таким образом, для (первоначального) построения правильно запол­ненного дерева необходимо выполнить следующее:

for!:=(Граница div 2) downto 1 do Sift(I,Граница);

(для примера на рисунке этот цикл выполняет все 4 прохода).

Итак, нами выполнена первая часть алгоритма – построение дере­ва^[24]. Перенесём максимальный элемент в конец массива (на своё место), и далее будем рассматривать дерево (массив), содержащие на 1 вер­шину (элемент) меньше. В начало массива (т.е. в корень дерева) при этом обмене записывается число из конца массива. Это – не обязательно ми­нимальный элемент массива, но, поскольку последний элемент массива есть лист дерева, полученное после такой перестановки дерево – скорее всего не будет правильно заполненным.

Но: где нарушается определение правильной заполненности? Только в корне! А с похожей ситуацией мы уже встречались - на последнем проходе при первоначальном построении дерева, и умеем её обрабаты­вать. (Теперь становится понятным смысл введения второго параметра процедуры Sift – ГраницаПоддерева.) В итоге мы получаем следующую про­цедуру сортировки методом HeapSort (дочерняя процедура Sift в тексте опущена):

procedure HeapSort (Граница: word);

var I: word;

begin

for!:=(Граница div 2) downto 1 do Sift(I,Граница); for!:=Граница downto 2 do begin

Обмен(1,I);

Sift (1,I-1);

end;

end;

Отметим, что при наличии в массиве нескольких одинаковых элемен­тов приведённый алгоритм может содержать лишние действия, поэтому, может быть, второй цикл лучше записать таким образом:

for I:=Граница downto 2 do

if Упорядочили(1,I) then Sift(1,I-1);

Рассмотрим второй цикл на старом примере (начнём с того момента, когда мы правильно заполнили дерево). На рисунке показаны границы между отсортированной и неотсортированной частями массивов (отсортированная часть- справа), а работа процедуры Sift показана «конспек­тивно» (участвующие в «просеивании» элементы выделены):

 

 

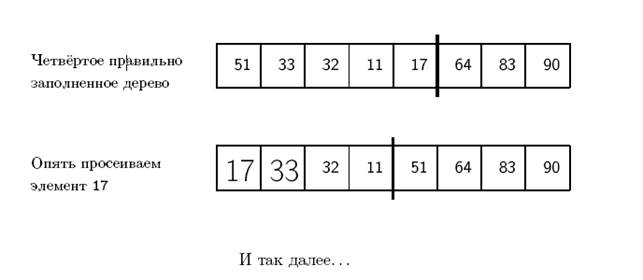
Оценим эффективность метода HeapSort. Отметим, что вовсе не оче­видно, что такой сложный алгоритм сортировки даёт хорошие результаты. Однако из очень простых рассуждений следует, что эффектив­ность метода (как число сравнений, так и число обменов – в этом ал­горитме будем оценивать их одновременно) пропорциональна n* logn. Действительно, число операций, необходимых для «просеивания элемен­та через правильное дерево, содержащее к элементов, пропорционально глубине этого дерева, т.е. log к. Таким образом, число операций и для первой, и для второй частей алгоритма пропорционально

В итоге получаем эффективность метода ~n*logn, что лу чш е, чем у любого из методов, рассмотренных ранее.

 

 

5.2 «Быстрая» сортировка

Как и для предыдущего метода, будем иногда употреблять английское сокращение названия - QuickSort.

Аналогично дихотомии, QuickSort тоже является одним из алгорит­мов группы «разделяй и властвуй». При поиске методом дихотомии мы делили рассматриваемый массив (примерно) пополам, чтобы искать нужный элемент только в одной половине. Нельзя ли здесь осуществить аналогичную идею –поставить элемент с номером на место, слева от него записать меньшие элементы, справа – большие, после чего сортировать две половины массива независимо друг от друга? В принципе это возможно, но алгоритмы поиска элемента с номером (т.н. медианы) сложны. Однако существуют достаточно простые алгорит­мы постановки на своё место произвольно выбранного элемента массива (например, первого по счёту), причём такой постановки, что в получен­ном массиве все элементы с меньшими номерами не больше рассмат­риваемого, и наоборот, все элементы с боль ши ми номерами не меньше рассматриваемого. Один из таких алгоритмов будет описан ниже.

Поставив таким образом выбранный элемент на место, будем сорти­ровать две части массива независимо друг от друга^[25]. И уже сейчас мы можем сказать, что, к сожалению, эффективность «в худшем» рассмат­риваемого метода сортировки пропорциональна п² (как у простых мето­дов): действительно, если массив в самом начале работы уже упорядо­чен, то работа рассматриваемого алгоритма практически не отличается от работы алгоритма прямого выбора. А название QuickSort было дано методу за хорошую эффективность «в среднем» (подробнее см. ниже).

Итак, опишем алгоритм такой постановки на место выбранного эле­мента, что в полученном массиве все элементы с меньшими номерами не больше рассматриваемого, и наоборот. Выберем первый элемент мас­сива; предположим, что он уже находится на своём месте. Чтобы это подтвердить (или опровергнуть), необходимо, вообще говоря, сравнить его со всеми оставшимися элементами массива; будем перебирать их «справа налево» (т.е. от больших номеров к меньшим). Если при этом найдётся “неправильный” элемент (т.е. не удовлетворяющий сделанно­му предположению о том, что все элементы справа от первого больше него), то придётся поменять местами этот элемент и первый. Основная идея алгоритма: будем предполагать, что рассматриваемый нами эле­мент (быв ши й первый, ниже – «главный») теперь находится на своём месте (т.е. больше всех элементов, стоящих слева от него). Заметим, что для проверки этого условия нужно сравнить его только с элементами, стоящими между его новым и старым положениями в массиве. Про­должая этот процесс (т.е. после каждого обмена предполагая, что глав­ный элемент уже находится на своём месте), мы каждый раз уменьшаем число элементов, необходимых для проверки сделанного предположения (это число уменьшается по крайней мере на 1), т.о. описанный алгоритм постановки элемента на место конечен.

Продемонстрируем работу алгоритма на примере. Главный элемент (51) всюду выделен крупным шрифтом и обведён в кружок. Направление сравнения показано стрелкой. Элемент, с которым обменивается главный, также выделен крупным шрифтом. Как обычно, жирными линиями показаны границы между частями массива: между двумя просмотренными и одной непросмотренной.

 

Итак, элемент 51 находится на своём месте, причём слева от него стоят меньшие элементы, а справа - большие.

Теперь несложно написать процедуру для алгоритма QuickSort. Ещё раз отметим, что она содержит рекурсивные (само)вызовы.

procedure QuickSort (Левый,Правый: word);

label 10,20,30;

begin

if Левый>=Правый then exit;

Л:=Левый; П:=Правый;

10: while Л<П do

if Упорядочили(Л,П)

then begin inc(Л); goto 20; end

else dec(П);

goto 30;

20: while Л<П do

if Упорядочили(Л,П)

then begin dec(П); goto 10; end

else тс(Л);

30: QuickSort(Левый,Л-1); QuickSort(П+1, Правый);

end;

Несмотря на неоднократное использование оператора goto, написан­ная нами процедура, по-видимому, удовлетворяет основным требованиям структурного программирования. Действи­тельно, в тексте явно выделены 3 подзадачи – движение налево, дви­жение направо и рекурсивный вызов. Если же обилие goto покажется нежелательным, то приведённый далее альтернативный вариант^[26] дол­жен удовлетворить самых взыскательных приверженцев канонов струк­турного программирования:

procedure QuickSort (Левый,Правый: word);

var Л,П: word;

Направо,У: boolean;

begin

if Левый>=Правый then exit;

Л:=Левый; П:=Правый;

Направо:=true;

repeat

У:=Упорядочили(Л,П);

if У=Направо then inc^) else dec(n);

if У then Направо:=not Направо;

until Л>=П;

QuickSort (Левый,Л-1); QuickSort(П+1,Правый);

end;

Для удобства желательно написать следующую процедуру Sort глобаль­ную по отношению к QuickSort:

procedure Sort (Граница: word);

begin

QuickSort(1,Граница);

end;

Выше было отмечено, что эффективность «в худшем» у метода QuickSort не лучше, чем у простых методов сортировки, и преимущество рассмотренного метода можно увидеть только «в среднем». Однако точно посчитать эффективность «в среднем» довольно сложно (это тоже было замечено ранее, в разделе 2), но на помощь приходит следующее сооб­ражение. Выбранный элемент массива может с равными вероятностями оказаться 1-м, 2-м,..., n-м, поэтому если знать количество операций (сравнений и/или пересылок), необходимых для обработки массивов раз­мерностей 1, 2,...,п– 1 (пусть для размерности i это число есть C _i), то несложно найти усреднённое число операций для массива размерности n:

Отметим, что в последней формуле учитывается и число операций (так­же – сравнений и/или пересылок) необходимых для реализации описан­ного выше подалгоритма постановки выбранного элемента на своё место: это – слагаемое n‑1.

Приведённая формула хорошо оценивает эффективность метода (чи­тателю полезно проверить это самостоятельно). Однако программа под­счёта эффективности по такой формуле (точнее – программа сравнения количества операций, необходимых «в среднем» для сортировки массива размерности n, с числом n*logп) не относится к рассматриваемой нами теме «сортировка массива». Эта программа будет приведена в части 2 на­стоящего пособия, при описании способов преобразования рекурсивных алгоритмов в нерекурсивные. Отметим ещё, что при сравнении эффек­тивности «в среднем» алгоритмов HeapSort и QuickSort (например, мето­дом случайного выбора начального массива) преимущество оказывается у последнего метода: коэффициент при n*logп для него оказывается меньше. (Провести такое сравнительное исследование двух методов сор­тировки читателю также полезно самостоятельно.)

 

Литература

1. Абрамов С. Лекции о сложности алгоритмов – М.: МЦНМО, 2009.

2. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы.
– М.: Вильямс, 2001

3. Алексеев В. Введение в теорию сложности алгоритмов. – М.: Изд-во ВМиК МГУ, 2002

4. Алексеев В., Таланов В. Графы и алгоритмы. Структуры данных. Модели вычислений. – М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория знаний, 2006

5. Вирт Н. Алгоритмы и структуры данных. – М.: Мир, 1989.

6. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. – М: Финансы и статистика; ИНФРА-М, 2009.

7. Головешкин В, Ульянов М. Теория рекурсии для программистов – М.: ФИЗМАТЛИТ, 2006

8. Громкович Ю. Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости,теорию сложности, теорию алгоритмов, теорию связи, и криптографию. – СПб.: БХВ, 2010.

9. Кормен Т., Лейзерсон Ч, Ривест Р. Алгоритмы: построение и анализ.- М: Вильямс, 2006

10. Кнут Д. Искусство программирования, том 1. Основные алгоритмы – М.: Вильямс, 2006.

11. Крупский В. Введение в сложность вычислений. – М.: Факториал Пресс, 2006

12. Левитин А. Алгоритмы: введение в разработку и анализ алгоритмы – М.: Вильямс, 2006.

13. Липский В. Комбинаторика для программистов. – М.: Мир,1989

14. Макконнелл Дж. Основы современных алгоритмов М.: Техносфера, 2004

15. Немнюгин С. Turbo Pascal. Программирование на языке высокого уровня – СПб.: Питер, 2007

16. Окулов С. Программирование в алгоритмах – М.:Бином, 2004

17. Сапоженко А. Некоторые вопросы сложности алгоритмов. - М.: Изд-во ВМиК МГУ, 2001

18. Харари Ф. Теория графов – М.: КомКнига, 2006

19. Шень А. Программирование: теоремы и задачи, – М., Изд-во МЦНМО, 1995.

20. Яблонский С. Введение в дискретную математику, –М.: Высшая школа, 2003.

 

^[1] Таким образом, для строгого определения эффективности необходимо иметь определение размерности. В каждом конкретном случае определение размерности своё. Применительно к рассматриваемым нами задачам сортировки и поиска, раз­мерность задачи - это просто размерность массива, т.е. Граница. Ниже это обозначе­ние будет употребляться в текстах программ и их фрагментов, а в формулах вместо Граница будем писать n.

^[2]Отметим ещё раз, что мы не будем использовать дополнительную память для сортировки массива.

^[3] В рассматриваемых в данном пособии примерах в качестве таких операций удоб­но выбрать сравнение и пересылку элементов, но иногда имеет смысл выбирать “более сложные” операции - подалгоримы. Например, в большинстве алгоритмов сортиров­ки массива можно было бы подсчитывать число обменов (вместо числа пересылок): ведь обмен двух элементов – простейший алгоритм.

^[4]В задачах сортировки массивов в качестве такого множества входов обычно рас­сматривается множество перестановок чисел от 1 до n.

^[5]Например, минимальная размерность, при которой среднее время работы «мед­ленного» алгоритма ОбменыМ (раздел 4.3) более чем на 10% превышает время работы “быстрого” алгоритма QuickSort (раздел 5.2), равна 8. А для размерно­стей, не превышающих 5, алгоритм ОбменыМ работает даже быстрее. Числа 5 и 8 - могут, конечно, немного изменяться в зависимости от конкретного способа проверки, но это непринципиально.

^[6]Ещё один интересный (и при этом несложный) пример удачного применения ал­горитма “разделяй и властвуй” (не связанный, однако, с рассматриваемыми здесь темами) - одновременный поиск минимума и максимума в массиве. См., например, [5].

^[7]Отметим, что обычно в литературе по информатике все логарифмы рассматри­ваются по основанию 2, поэтому основание логарифмов опускается. Есть ещё одно объяснение: для перехода к логарифму по другому основанию ( a ) достаточно при­менить умножение на константу (log₀ 2).

^[8]Однак<