Правило Лопиталя. Примеры.

Метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

На промежутке [a;b] заданы две функции и , имеющие производные, причём f(a)=g(a)=0. Т.к. эти фу-ции имеют производные, то они непрерывны, а потому и при .

Значит если предел отношения производных существует.

используя теорему Коши(Теорема Коши. , где C (a,b) ), получим , где a<c<x

Ясно, что при , поэтому

Но

Значит,

Примеры:

1.)

2.) 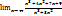= “можно применить правило Лопиталя 3 раза (а лучше разделим на x ³)”

=

Билет 31

Условия возрастания и убывания функции.

· Функция называется возрастающая на промежутке Х, если любой x₁, x₂ принадлежит X при том, что x₁<x₂, следовательноf(x₁)<f(x₂)

· Функция называется неубывающей на промежутке Х, если любой x₁, x₂ принадлежит X при том, что x₁<x₂, следовательноf(x₁)≤f(x₂)

· Функция называется возрастающая на промежутке Х, если любой x₁, x₂ принадлежит X при том, что x₁<x₂, следовательноf(x₁)>f(x₂)

· Функция называется возрастающая на промежутке Х, если любой x₁, x₂ принадлежит X при том, что x₁<x₂, следовательноf(x₁)≥f(x₂)

Достаточное условие.

1) Если функция f(x) дифференцируема в точке x₀, f’(x₀)=0 и f’(x) меняет знак через точку x₀, то f(x) в точке x₀ имеет экстремум.

Если f’(x) при переходе через точку x₀ меняет знак с + на -, то x₀ точка максимума, а если с – на +, то x₀ точка минимума.

2)Если функция f(x) дважды дифференцируема в точке x₀, f’(x₀)=0 и f’’(x₀)≠0, то в точке x₀ функция имеет максимум при f’’(x₀)<0, если f’’(x₀)>0, то f(x) минимум.

 

 

Вопрос 29

Теорема Коши.

Пусть даны две функции С, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b)

- производные и не обращаются в ноль одновременно на интервале (a,b)

- тогда

, где C (a,b)

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля “(Теорема Ролля:Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.)”: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а равна как раз необходимому числу.

Вопрос 28

Теорема Лагранжа.

Если f(x) непрерывна на [a;b] и дифференцируема на [a;b], то существует точка c, принадлежащая отрезку [a;b], такая что справедливо равенство

F(b)-f(a)=(b-a)*f `(c)

Доказательство:

Соединим AB

Начинаем двигать AB (До касательной параллельной AB)

Касательная параллельна AB =>tgα=tgβ (α=β)

= f `(c) BD = f(b)-f(a) AD = b-a

Следствие.

Если f(x) имеет f `(x) на [a;b], то внутри промежутка найдется точка c, в которой будет выполнятся равенство (Формула конечного приращения):

Вопрос 27

Теорема Рὁлля.

Если функция f (х) непрерывна на отрезке а ≤ х ≤ b, имеет внутри его определённую производную, а на концах принимает равные значения f (a) = f (b), то её производная f ' (x) по меньшей мере один раз обратится в нуль в интервале (a, b),

т. е. существует такое с (где a < с < b), что f’ (с) = 0. Как следствие получается, что между двумя последовательными корнями функции имеется хотя бы один корень её производной.

 

. Функция f(x) постоянна на интервале [ а, b ]; тогда f ' (с) = 0 для любого с (a < с < b), т.е. утверждение теоремы Ролля выполняется автоматически.

 

 

Вопрос 26

Т. Ферма

f(x) принимает наименьшее или наибольшее значение во внутр. Тчк. «С» промежутка «Х»

Э f’(c)=>f’(c)=0

m₀<=f’(x)<=M₀

 

Если сущ. Производная зн. Сущ. Касательная
f’(x₀)=tgL=k

1)

Док-тьтеор. Если в тчк. «С» наименьшее знач.

По треор. О пред. Переходе в нерав.

2)

 

Вопрос 25

Функция заданная параметрически

Пусть зависимость между аргументом Х и функцией У задана параметрически в виде двух уравнений

(1)

где t – вспомогательная переменная, называемая параметром. Найдём производную , считая, что функции (1) имеют производные и что функция x = x(t) имеет обратную t = 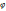(x). По правилу дифференцирования обратной функции

(2)

Функцию y = f(x), определяемую параметрическими уравнениями (1), можно рассматривать как сложную функцию y = y(t), где t= (x).

По правилу дифференцирования сложной функции имеем: .

С учётом равенства (2) получаем

Полученная формула позволяет находить производную от функции заданной параметрически, не находя непосредственной зависимости У от Х.

Пример:

Пусть Найти

Решение: Имеем Следовательно, , т.е. .

В этом можно убедиться, найдя непосредственно зависимость от Х

Действительно, t = . Тогда . Отсюда , т.е. .

Вопрос 24

Параметрическое уравнение линии на плоскости

Параметрич. Ур-е окружности

Пусть в прямоугольной системе координат дана окружность

Рассмотрим ее произвольную точку M(x;y)

Пусть радиус-вектор точки М образует угол величины t с положительным направлением оси ОХ, тогда абсцисса и ордината точки Мизменяются в зависимости от t (0 ). Выражая х и у через t, находим

(0 )