Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
Вывод формул для нахождения коэффициентов. Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 
по переменным а и b, приравниваем эти производные к нулю.
Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК). 
При данных а и b функция 
принимает наименьшее значение.
Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы 
, 
, 
, 
и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a.
Основная сфера применения таких полиномов - обработка экспериментальных данных (построение эмпирических формул). Дело в том, что интерполяционный полином, построенный по значениям функции, полученным с помощью эксперимента, будет испытывать сильное влияние "экспериментального шума", к тому же при интерполировании узлы интерполяции не могут повторяться, т.е. нельзя использовать результаты повторных экспериментов при одинаковых условиях. Среднеквадратичный же полином сглаживает шумы и позволяет использовать результаты многократных экспериментов.
Численное интегрирование и дифференцирование. Пример.
Численное интегрирование – вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.
Численное дифференцирование – совокупность методов вычисления значения производной дискретно заданной функции.
Интегрирование
Постановка задачи. Математическая постановка задачи: необходимо найти значение определенного интеграла
где a, b - конечны, f(x) - непрерывна на [а, b].
При решении практических задач часто бывает, что интеграл неудобно или невозможно взять аналитически: он может не выражаться в элементарных функциях, подынтегральная функция может быть задана в виде таблицы и пр. В таких случаях применяют методы численного интегрирования. Численные методы интегрирования используют замену площади криволинейной трапеции на конечную сумму площадей более простых геометрических фигур, которые могут быть вычислены точно. В этом смысле говорят об использовании квадратурных формул.
В большинстве методов используется представление интеграла в виде конечной суммы (квадратурная формула):
В основе квадратурных формул лежит идея замена на отрезке интегрирования графика подынтегрального выражения функциями более простого вида, которые легко могут быть проинтегрированы аналитически и, таким образом, легко вычислены. Наиболее просто задача построения квадратурных формул реализуется для полиномиальных математических моделей.
Можно выделить три группы методов:
1. Метод с разбиением отрезка интегрирования на равные интервалы. Разбиение на интервалы производится заранее, обычно интервалы выбираются равными (чтобы легче было вычислить функцию на концах интервалов). Вычисляют площади и суммируют их (методы прямоугольников, трапеции, Симпсона).
2. Методы с разбиением отрезка интегрирования с помощью специальных точек (метод Гаусса).
3. Вычисление интегралов с помощью случайных чисел (метод Монте-Карло).
Метод прямоугольников. Пусть функцию (рисунок) необходимо проинтегрировать численным методом на отрезке [a,b]. Разделим отрезок на N равных интервалов. Площадь каждой из N криволинейных трапеций можно заменить на площадь прямоугольника.
Ширина всех прямоугольников одинакова и равна:
В качестве выбора высоты прямоугольников можно выбрать значение функции на левой границе. В этом случае высота первого прямоугольника составит f(a), второго – f(x1),…, N-f(N-1).
Если в качестве выбора высоты прямоугольника взять значение функции на правой границе, то в этом случае высота первого прямоугольника составит f(x1), второго – f(x2), …, N – f(xN).
Как видно, в этом случае одна из формул дает приближение к интегралу с избытком, а вторая с недостатком. Существует еще один способ – использовать для аппроксимации значение функции в середине отрезка интегрирования:
. -оценка абсолютной погрешности метода прямоугольников (середина)
- оценка абсолютной погрешности методов левых и правых прямоугольников.
Пример. Вычислить для всего интервала и с делением интервала на четыре участка
. 
Решение. Аналитическое вычисление данного интеграла дает I=агсtg(1)–агсtg(0)=0,7853981634. В нашем случае:
1)h = 1; xо = 0; x1 = 1; 
2) h = 0,25 (1/4); x0 = 0; x1 = 0,25; x2 = 0,5; х3 = 0,75; x4 = 1;
Вычислим методом левых прямоугольников:
Вычислим методом правых прямоугольников:
Вычислим методом средних прямоугольников:
Метод трапеций. Использование для интерполяции полинома первой степени (прямая линия, проведенная через две точки) приводит к формуле трапеций. В качестве узлов интерполирования берутся концы отрезка интегрирования. Таким образом, криволинейная трапеция заменяется на обычную трапецию, площадь которой может быть найдена как произведение полусуммы оснований на высоту
В случае N отрезков интегрирования для всех узлов, за исключением крайних точек отрезка, значение функции войдет в общую сумму дважды (так как соседние трапеции имеют одну общую сторону)
Формула трапеции может быть получена, если взять половину суммы формул прямоугольников по правому и левому краям отрезка:
Проверка устойчивости решения. Как правило, чем меньше длина каждого интервала, т.е. чем больше число этих интервалов, тем меньше различаются приближенное и точное значение интеграла. Это справедливо для большинства функций. В методе трапеций ошибка вычисления интеграла ϭ приблизительно пропорциональна квадрату шага интегрирования (ϭ ~ h2).Таким образом, для вычисления интеграла некоторой функции в переделах a,b необходимо разделить отрезок [a,b] на N0 интервалов и найти сумму площадей трапеции. Затем нужно увеличить число интервалов N1, опять вычислить сумму трапеции и сравнить полученное значение с предыдущим результатом. Это следует повторять до тех пор (Ni), пока не будет достигнута заданная точность результата (критерий сходимости).
Для методов прямоугольников и трапеции обычно на каждом шаге итерации число интервалов увеличивается в 2 раза (Ni+1=2Ni).
Критерий сходимости:
Главное преимущество правила трапеций – его простота. Однако если при вычислении интеграла требуется высокая точность, применение этого метода может потребовать слишком большого количества итераций.
Абсолютная погрешность метода трапеций оценивается как
.
Пример. Вычислить приближенно определенный интеграл по формуле трапеций. 
а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.
Решение:
а) По условию отрезок интегрирования нужно разделить на 3 части, то есть 
.
Вычислим длину каждого отрезка разбиения: 
.
Таким образом, общая формула трапеций сокращается до приятных размеров:
Окончательно:
Напоминаю, что полученное значение – это приближенное значение площади.
б) Разобьём отрезок интегрирования на 5 равных частей, то есть 
. увеличивая количество отрезков, мы увеличиваем точность вычислений.
Если , то формула трапеций принимает следующий вид:
Найдем шаг разбиения:
, то есть, длина каждого промежуточного отрезка равна 0,6.
При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:
В первой строке записываем «счётчик»
В результате:
Ну что же, уточнение, и серьёзное, действительно есть!
Если для 3-х отрезков разбиения 
, то для 5-ти отрезков 
. Если взять еще больше отрезком => будет еще точнее.
Формула Симпсона. Формула трапеции дает результат, сильно зависящий от величины шага h, что сказывается на точности вычисления определенного интеграла особенно в тех случаях, когда функция имеет немонотонный характер. Можно предположить повышение точности вычислений, если вместо отрезков прямых, заменяющих криволинейные фрагменты графика функции f(x), использовать, например, фрагменты парабол, приводимых через три соседние точки графика. Подобная геометрическая интерпретация лежит в основе метода Симпсона для вычисления определенного интеграла. Весь интервал интегрирования a,b разбивается N отрезков, длина отрезка также будет равна h=(b-a)/N.
Формула Симпсона имеет вид:
остаточный член
С увеличением длины отрезков точность формулы падает, поэтому для увеличения точности применяют составную формулу Симпсона. Весь интервал интегрирования [a,b] разбивается на четное число одинаковых отрезков N, длина отрезка также будет равна h=(b-a)/N. Составная формула Симпсона имеет вид:
В формуле выражения в скобках представляют собой суммы значений подынтегральной функции соответственно на концах нечетных и четных внутренних отрезков.
Остаточный член формулы Симпсона пропорционален уже четвертой степени шага:
Пример: Пользуясь правилом Симпсона вычислить интеграл 
. (Точное решение - 0,2)
Для n = 1
Для n = 2
Правило Симпсона позволяет точно рассчитать интеграл не только от квадратичной функции, но и для полинома третей степени
.
Метод Гаусса
Квадратурная формула Гаусса. Основной принцип квадратурных формул второй разновидности виден из рисунка 1.12: необходимо так разместить точки х 0 и х 1 внутри отрезка [ a; b ], чтобы площади "треугольников" в сумме были равны площади "сегмента". При использовании формулы Гаусса исходный отрезок [ a; b ] сводится к отрезку [-1;1] заменой переменной х на
0.5∙(b – a)∙ t + 0.5∙(b + a).
Тогда 
, где 
.
Такая замена возможна, если a и b конечны, а функция f (x) непрерывна на [ a; b ]. Формула Гаусса при n точках xi, i =0,1,.., n -1 внутри отрезка [ a; b ]:
, (1.27)
где ti и Ai для различных n приводятся в справочниках. Например, при n =2 
A 0= A 1=1; при n =3: t 0 =t 2»0.775, t 1=0, A 0 =A 2»0.555, A 1»0.889.
Квадратурная формула Гаусса
получена с весовой функцией равной единице p(x)= 1 и узлами xi, являющимися корнями полиномов Лежандра
Коэффициенты Ai легко вычисляются по формулам
i =0,1,2,... n.
Значения узлов и коэффициентов для n=2,3,4,5 приведены в таблице
| Порядок | Узлы | Коэффициенты |
| n =2 | x1 =0 x0= - x2 =0.7745966692 | A1 =8/9 A0=A2 =5/9 |
| n =3 | x2= - x1 =0.3399810436 x3= - x0 =0.8611363116 | A1=A2 =0.6521451549 A0=A3 =0.6521451549 |
| n=4 | x 2 = 0 x 3 = - x 1 = 0.5384693101 x 4=- x 0=0.9061798459 | A 0=0.568888899 A 3= A 1=0.4786286705 A 0= A 4=0.2869268851 |
| n =5 | x 5 = - x 0=0.9324695142 x 4 = - x 1=0.6612093865 x 3 = - x 2=0.2386191861 | A 5 =A 0=0.1713244924 A 4 =A 1=0.3607615730 A 3 =A 2=0.4679139346 |
Пример. Вычислить значение 
по формуле Гаусса для n =2:
,
Точное значение: 
.
Алгоритм вычисления интеграла по формуле Гаусса предусматривает не удвоение числа микроотрезков, а увеличение числа ординат на 1 и сравнение полученных значений интеграла. Преимущество формулы Гаусса – высокая точность при сравнительно малом числе ординат. Недостатки: неудобна при расчетах вручную; необходимо держать в памяти ЭВМ значения ti, Ai для различных n.
Погрешность квадратурной формулы Гаусса на отрезке будет 
при этом 
Для 
формула остаточного члена будет 
причем коэффициент α N быстро убывает с ростом N. Здесь 
Формулы Гаусса обеспечивают высокую точность уже при небольшом количестве узлов (от 4 до 10) В этом случае 
В практических же вычислениях число узлов составляет от нескольких сотен до нескольких тысяч. Отметим также, что веса квадратур Гаусса всегда положительны, что обеспечивает устойчивость алгоритма вычисления сумм
Дифференцирование. При решении задач часто бывает необходимо найти производную определенного порядка от функции f(x), заданной таблично. Кроме того, иногда в силу сложности аналитического выражения функции f(x) ее непосредственное дифференцирование слишком затрудненно, а также при численном решении дифференциальных уравнений. В этих случаях используют численное дифференцирование.
Выведем некоторые из формул численного дифференцирования. Рассмотрим разложения в ряд Тейлора
(1)
. (2)
Здесь 
– величина порядка 
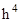(С – некоторая постоянная). Из (1) найдем
(3)
где 
– величина порядка h.
Аналогично из (2) можно получить
. (4)
Вычтем из выражения (1) соотношение (2)
. (5)
Отсюда имеем
. (6)
Складывая выражения (1) и (2), найдем
(7)
Из (7) получим
(8)
Из равенств (3), (4), (6) и (8) вытекают следующие приближенные формулы для вычисления производных функции f(x) в точке 
, которые называют формулами численного дифференцирования:
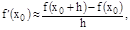(9)
(10)
(11)
(12)
Формулы (9) и(10) имеют первый порядок точности по h, так как их погрешность пропорциональна h. Формулы (11) и (12) имеют второй порядок точности по h, так как их погрешность пропорциональна 
. Используя разложения в ряд Тейлора функций 
и т. д. можно получить более точные формулы для вычисления первой и второй производных, а так же формулы для вычисления производных высших порядков.
Геометрическая иллюстрация формул (9) и (11).
Пример. Дана функция f(x). Найти приближенное значение первой и второй производной по формулам численного дифференцирования при различных значениях h и сравнить с точными значениями.
Пусть 
.
Положим 
Вычислим первую производную:
Точное значение: 
Вычислим вторую производную: 
Точное значение: 
Положим 
Вычислим первую производную:
Для первой производной результаты, найденные при h=0.01, ближе к точному значению чем результаты, найденные при h=0.1.
Вычислим вторую производную: 
(7)
Замечание: Формулы численного дифференцирования очень чувствительны к ошибкам округления. При их использовании следует вычислять значение функции f(x) с большим числом значащих цифр (особенно при малых h). Формула (7) при дает грубый результат, хотя она же при дает неплохой результат. Если в (7) значения функции f(x) вычислить с точностью до 8 цифр после запятой (было 5 цифр), то результат будет отличным:
