В симметричной двойственной задаче, как и в прямой задаче, ограничения задаются в виде неравенств и компоненты вектора не отрицательны.
Замечание. Если в двойственной задаче целевая функция исследуется на min, то система ограничений указывается в виде неравенств 
Замечание. Если в двойственной задаче целевая функция исследуется на max, то система ограничений указывается в виде неравенств 
Вопрос 8. Метод северо-западного угла
Согласно этому методу запасы очередного Поставщика используются для обеспечения запросов очередных Потребителей до тех пор, пока не будут исчерпаны полностью. После чего используются запасы следующего по номеру Поставщика.
Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного Поставщика и запросов очередного Потребителя заполняется только одна клетка и соответственно исключается из рассмотрения один Поставщик или Потребитель.
Во избежании ошибок после построения начального базисного (опорного) решения необходимо проверить, что число занятых клеток равно m+n-1.
Вопрос 9. Метод потенциалов
Если допустимое решение Х =(
) i=1, 2,…m, j=1,2,…n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков 
(i=1, 2,…m) и потребителей 
(j=1,2,…n), удовлетворяющие следующим условиям
Группа равенств (1) используется как система уравнений
для нахождения потенциалов.
Так как число неизвестных системы на единицу больше числа уравнений,
то одной из них можно задать значение произвольно, а остальные найти
из системы.
Группа неравенств (2) используется для проверки оптимальности опорного решения. Эти неравенства удобнее представить в следующем виде
Числа 
называются оценками для свободных клеток таблицы (векторов условий) транспортной задачи.
Вопос 10 Пример игры с 2 пальцами.
Два игрока показывают 1 или 2 пальца, при этом предполагают – какое кол-во пальцев укажет противник.
I II
1 2
предположение предположение
II 1 I 2
Рассмотрим все возможные стратегии(конечное число).
(I, II): 1) (1,1) 2) (1,2) 3) (2,1) 4) (2,2)
Аналогично рассматриваются 2 игрока А 4х4
а11 а12 а13 а14
а21 а22 а23 а24
А = а31 а32 а33 а34
а41 а42 а43 а44
а 11 – выигрыш I игрока, при условии, что I принимает 1) и II принимает 1) стратегии
а 12 – выигрыш I игрока, при условии, что I применит 1) стратегию, а II – 2) стратегию.
I II
1 2
II 1 I 1
Выигрыш II игрока 1+2=3
а13 = выигрыш I игрока.
Вопрос 11 12 Чистая Нижняя и верхняя цена игры.
Пусть 1 игрок имеет m стратегий,2 игрок n стратегий.
Матрица выигрыша 1 игрока
min 
(I =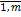 
)
j
max min = 
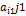=α(*)
I j
Определение: Чистой нижней ценой игры наз-ся число α,определенное по формуле(*)
Max (j= 
I
max min = 
=β(**)
I j
Определение: Чистой верхней ценой игры наз- ся числа β,определенные по формуле (**)
Вопрос 13. Седловая точка
Седловой точкой игры называют точку, в кот α=β. Решением матричной игры наз.седловая точка или седловой элемент.
Седловой точкой (хₒ;уₒ) для функции f(х,у) называется точка, удовлетворяющая неравенству:
F(x,yₒ)≤f(xₒ,yₒ)≤f(xₒ,y)
Для любого х, у. (хєА;yєB)
Вопрос 14. Оптимальные чистые стратегии.
На промышленных предприятиях теория игр может применяться для выбора оптимальных решений, например при создании рациональных запасов трудовых ресурсов, сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличения запасов, гарантирующих бесперебойную работу про-ва, и сокращения запасов в целях минимизации затрат на их хранение. В с/х теория игр может применяться при решении таких экономических задач, как выбор посева одной из возможных культур, урожай которой зависит от погоды, если известна цена единицы той или иной культуры и средняя урожайность каждой культуры в зависимости от погоды. В этом случае одним из игроков является с/х предприятие, стремящееся обеспечить наибольший доход, а другим - природа.
Решение подобных задач требует полной определенности в формулировании их условий(правил игры): установлении кол-ва игроков, выявления возможных стратегий игроков и возможных выигрышей.
Важным элементом в условии игровых задач является стратегия – совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а её элементы – чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные.
Понятия оптимальной стратегии, цены игры, среднего выигрыша находят отражение в определении решения игры: стратегии P* и Q* первого и второго игроков соответственно называются их оптимальными стратегиями, а число V – ценой игры, если для любых стратегий P первого игрока и любых стратегий Q второго игрока выполняются неравенства:
M(P,Q*)≤V≤M(P*,Q),где M(P,Q) означает математическое ожидание выигрыша первого игрока, если первым и вторым игроками избраны соотв. Стратегии P и Q.
Из данного неравенства следует, что V=M(P*,Q), т.е. цены игры равна математическому ожиданию выигрыша первого игрока, если оба игрока изберут для себя оптимальные стратегии.
Вопрос 15. Смешанные стратегии
Смешанными стратегиями игрока наз. перечень вероятностей, с кот. игрок применит свои чистые стратегии.
Пусть 1й игрок имеет m чистых стратегий: 1,2,3,…,m
х-смешан.стратегия 1го игрока
х=(х1,х2,..., хm)
хi ≥0 ∑ х1 =1 i=1,m
Пусть 2й игрок имеет n чистых стратегий: 1,2,3,..,n