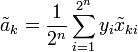В практической деятельности часто требуется оценить параметры некоторой системы, то есть построить её математическую модель и найти численные значения параметров этой модели. В качестве исходных данных для построения модели служат результаты эксперимента, который представляет собой совокупность нескольких измерений, выполненных по определённому плану. В простейшем случае план является описанием условий проведения измерений, то есть значения входных параметров (факторов) во время измерения. В качестве примера систем, оценка параметров которых актуальна с практической точки зрения, могут служить различные технологические процессы.
В общем случае отклик системы описывается некоторой функцией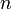 
переменных
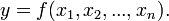
Математическая модель системы получается в результате апроксимации этой функции какой-либо другой функцией, например линейной
,
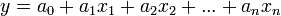где 
– искомые параметры модели.
На рисунке в графическом виде представлен процесс построения линейной модели процесса фотолитографии, где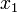 
– толщина плёнки фотоэмульсии, 
– время экспонирования, 
— разрешение, полученное в данных условиях. Функция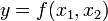 
нелинейна, однако в достаточной близости от точки 
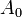её можно заменить касательной плоскостью 
. В показанной на рисунке области максимальная ошибка модели составляет 
.
Зная коэффициенты модели 
, можно с определённой точностью предсказывать значение функции (а значит и поведение системы) в окрестностях точки 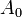. В определении значений коэффициентов и состоит цель эксперимента.
Матрица эксперимента
Расположение экспериментальных точек в двухмерном факторном пространстве
Предположим, исходные параметры технологического процесса составляют: толщина плёнки 55 мкм, время экспозиции – 30 с, то есть
Возьмём верхние и нижние значения обоих факторов так, чтобы они располагались симметрично относительно текущего значения, например
Составим таблицу, в которой значения обоих факторов находятся во всех возможных сочетаниях и проведём измерения в этих точках (значения отклика даны условно):
Полагая, что линейная модель процесса имеет вид
,
на основании полученных результатов можно составить систему четырёх уравнений с двумя переменными. Ниже показана эта система, а также её сокращённая запись в виде матрицы. Матрицу данного вида назовём матрицей эксперимента.
В матрице эксперимента второй и третий столбцы представляют собой значения факторов, четвёртый столбец – значения отклика системы, а первый столбец содержит единицы, соответствующие единичным коэффициентам свободного члена модели 
. Будем считать этот столбец некоторым виртуальным фактором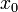 
, который всегда принимает единичные значения.
Решение системы
Переход к нормированным координатам
Чтобы облегчить решение системы, проведём нормировку факторов. Верхним значениям факторов присвоим нормированное значение +1, нижним значениям – нормированное значение –1, среднему значению – нормированное значение 0. В общем виде нормировка фактора выражается формулой
С учётом нормировки факторов система уравнений и матрица эксперимента примут следующий вид:
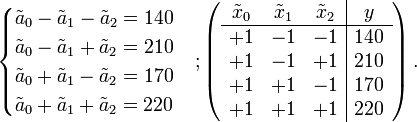
Поскольку сумма членов во втором и третьем столбце матрицы равны нулю, свободный член модели можно найти, сложив все четыре уравнения:
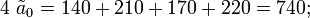
Чтобы найти какой-либо другой коэффициент модели, нужно изменить знаки в уравнениях таким образом, чтобы в соответствующем столбце оказались одни единицы, после чего сложить все четыре уравнения:
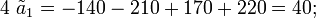
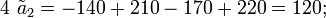
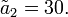
Таким образом, линейная модель технологического процесса в окрестностях точки (55, 30) имеет вид
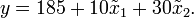
В общем случае решение системы будет выглядеть как
