Если задана какая-то таблица с экспериментальными данными x j и y j и нет никакой дополнительной информации, то определение вида эмпирической формулы представляет собой трудную задачу. Рассмотрим сначала случай, когда эмпирическая зависимость определяется формулой с двумя параметрами a и b, то есть
y = f (x; a, b) (4.13)
Если окажется, что
(4.14)
то искомая зависимость линейная, т.е.
y = ax + b 1 (4.15)
и задача легко решается.
Другим простым случаем является определение квадратичной зависимости
y = ax 2 + b (4.16)
путём построения графика на полуквадратической системе координат, на которой парабола (4.16) представляется прямой линией, а коэффициенты a и b легко находятся рассмотренными выше способами.
Рассмотрим общий случай, когда соотношение (4.13) не сводиться к формулам (4.15) и (4.16). Получим необходимое условие существования эмпирической зависимости вида (4.13) для заданной системы точек (x i, y i). Пусть M i(x i, y i), M j(x j, y j), M k(x k, y k) три точки значений из нашей совокупности. Предполагая, что кривая (4.13) проходит через точки M i, Mj и M k, будем иметь
y i = f (x i; a, b), yj = f (x j; a, b), y k = f (x k; a, b) (4.17)
Исключая из системы (4.17) параметры a и b, получим соотношение вида
Ф (x i, x j, x k, y i, y j, y k) = 0. (4.18)
Выполнение равенства (4.18) для любых значений i, j, k (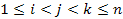
) необходимо для существования зависимости (4/13). Проверка соотношения (4.18) связана с трудоёмкими вычислениями, поэтому на практике ограничиваются одной тройкой точек: начальной (x 1, y 1), промежуточной (x S, y S) и конечной (x n, y n). Точку M S выбирают так, чтобы соотношение (4.18) было по возможности простым. Иногда точку M S выгодно брать не принадлежащую нашему ряду точек, тогда координаты x S, y S определяются интерполированием.
Пример. Получить необходимое условие для существования степенной зависимости
y = axk, (4.19)
предполагая, что x i > 0, y i > 0 (i =1,2,…, n).
Решение. Выберем
x S = 
.
Из формулы (4.19) имеем
y 1 = axb; y S = a 
= a 
, y n = a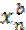 
(4.20)
Исключая из соотношения (4.20) параметры a и b получим
y 1 y n = a 
= a 2 
а от сюда следует, что y 1 y n = 
, т.е. 
.
Таким образом, для существования степенной зависимости (4.19) необходимо, чтобы среднему геометрическому x S значений х 1 и х n соответствовало среднее геометрическое y S значение y 1 и y n. Если x S не является табличным, то соответствующее значение y S определяется с помощью интерполирования.
Далее мы рассмотрим наиболее часто встречающиеся зависимости.
1. y = ax + b;
2. y = axb;
3. y = abx;
4. y = a + 
;
5. y = 
;
6. y = 
7. y = a ln x + b.
Аналогично тому как это было сделано выше в примере для существования зависимостей 1–7 можно вывести простые необходимые условия: 
и 
, где 
и 
. При этом предполагается, что х i > 0 и у i > 0. Эти выражения для и 
приведены в таблице 9.
Таблица 9
| № | 
| 
| Вид эмпирической формулы | Способ выравнивания |
| 1. |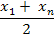 
(среднее арифметическое)
| 
(среднее арифметическое)
| y = ax + b | |
| 2. | 
(среднее геометрическое)
| 
(среднее геометрическое)
| y = ax 2 | Y = α + bX, где X = lg x, Y =lg y, α = lg a. |
| 3. |
|
| y = abx или
y = ae 
|
Y = α +  x,
где β = lg b, Y =lg y, α = lg a.
|
| 4. | 
| 
|
y = a + 
| Y = ax + b, где Y = xy |
| 5. | 
| 
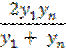
| y =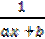 
| Y = ax + b, где
Y = 
|
| 6. | 
| 
| y = 
| Y= ax + b, где
Y = 
|
| 7. | 
|
| y = a ln x + b | Y = ax + b, где y = lg x |
Приведённая таблица 9 облегчает выбор эмпирической формулы среди указанных. Для проверки пригодности определённой эмпирической формулы, пользуясь исходными данными, находим значение и табличное значение 
и сравниваем его со значением ψ (
) = 
. Предпочтительнее та формула, для которой расхождение 
наименьшее.
Если значение ψ () = 
не находятся среди исходных данных x i, то отвечающее ему значение 
можно определить посредством линейной интерпретации
= 
+ 
( - 
),
где и 
– промежуточные значения, между которыми находиться 
.
Следует иметь ввиду, что описанный подход является грубо ориентированным, так как мы не учитываем поведение всех промежуточных точек (
). Кроме того, приведённая таблица эмпирических функций охватывает небольшое количество зависимостей и может случиться, что переменные х и у подчинятся некоторой закономерности, не вошедшей в наш список.
Следует так же учесть, что функции 1–7 монотонные, и, следовательно отвечающие им упорядоченные данные () при ∆ x i = x i+1 – x i > 0 (i = 1,2,…, n -1), должны обладать постоянным знаком приращения 
. Если это условие не выполняется, то зависимости 1–7 не могут использоваться в качестве эмпирических формул.
Пример. Определить вид эмпирической формулы, отвечающей следующей таблице 10.
Таблица 10:
| х | ||||||||
| у | 29,4 | 33,3 | 35,2 | 37,2 | 45,8 | 55,2 | 65,6 | 77,3 |
Решение. Будем искать эмпирическую формулу среди зависимостей 1–7, приведённых в таблице 9. Результаты вычислений приведены в таблице 11, из которой следует, что нужно выбрать степенную зависимость
y = axb.
Таблица 11
| № |
|
| 
| ( … )
| Вид формулы |
| 1. |
|
 =53,35
| 50,5 | 2,85 | y = ax + b мало подходит |
| 2. |
|
 =  = 47,7
| 48,7 | 1,0 | y = axb – подходит лучше других формул |
| 3. |
|
 = 47,7
| 50,5 | 2,8 | y = axb – мало подходит |
| 4. |
|
| 46,9 | 6,45 |
y = a +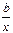 
не подходит
|
| 5. |
| 
| 50,5 | 7,9 |  не подходит
|
| 6. | 
| 
| 46,9 | 4,3 | y =  - не подходит
|
| 7. | 
| 
| 48,7 | 4,65 | y = a ln x + b не подходит |
4.7. Эмпирические формулы, содержащие три параметра.
В этом случае эмпирические формулы в общем виде записываются так
y = f (x; a,b,c),
где a, b и с – некоторые постоянные.
Первой формулой с тремя параметрами является квадратическая зависимость
y = ax 2 + bx + c. (4.21)
Критерий проверки экспериментальных данных на зависимость (4.21) существует. Но он строится с таки громоздкими расчётами и составлением сложной таблицы, что легче по экспериментальным данным построить кривую, как мы это уже делали, и убедиться, похожа ли она на зависимость (4.21).
Рассмотрим степенную зависимость вида
y = axb + c (4.22)
Отсюда y – c = axb. Логарифмируя это выражение получим
lg (y – c) = lg a + b lg x.
Полагая lg (y - c) = Y и lg x = X, получим линейную зависимость
Y = bX + lg a.
Определение параметров формулы (4.22) начнём с нахождения с. Для этого составим среднее геометрическое 
= 
, и, пользуясь графиком, построенным по исходным данным, или методом линейной интерполяции для 
, найдём соответствующее значение 
. Предполагая, что точки M 1(x 1, y 1), M S(x S, y S), M n(x n, y n) расположены на кривой (4.22), будем иметь три неравенства.
, 
, 
.
Возводя 
= 
в степень b и умножая на а, получим
a 
или y s – c = 
.
Решим последнее уравнение относительно с.
= 
; 
;
c (
) = 
; c = 
.
После этого строим точки N i(X i, Y i), где X i = lg x i, Y i = lg(y i – c) (i = 1,2,…, n). Если эти точки располагаются близко к прямой линии, то зависимость (4.22) выбрана правильно. Причём, постоянные а и b находятся обычным способом.
Пример. Для переменных х и у дана таблица 12
Таблица 12
| х | ||||||
| у | 0,10 | 0,28 | 0,80 | 1,38 | 2,56 | 4,10 |
Найти эмпирическую формулу, связывающую эти переменные коэффициентами a,b и с.
Решение. Построим эмпирическую формулу вида:
y = axb + c.
Находим
.
На графике, если его построить, этому значению соответствует 
= 0,507. Отсюда
c = 
.
Остальные параметры а и b найдём методом средних.
Составляем начальное уравнение с учетом, найденного значения с.
lg (y i – 0,048) = lg a + b lg x i, (i = 1,2,…,6)
Тогда будем иметь систему уравнений
-1,2840 = lg a + 2,3979 b; 0,1245 = lg a + 3,0792 b;
-0,6345 = lg a + 2,6990b; 0,4000 = lg a + 3,2041b;
-0,1238 = lg a + 2,9542 b; 0,6077 = lg a + 3,3010 b;
Группируя эти уравнения по три, получим
.
Вычитаем из первого уравнения второе: -3,1745 = 1,5332 b; b = 2,071.
.
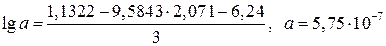Таким образом, искомая эмпирическая формула будет иметь вид.
y = 5,75 · 10-7 x 2,071 + 0,048.
Рассмотрим показательную зависимость
y = aebx + c (4.23)
Перенося слагаемое с влево и логарифмируя, получим
lg (y - c) = lg a + bxM,
где M = lg e = 0,434.
Таким образом,
Y = lg a + bMx, (4.24)
где y = lg(y – c).
Определим параметр с. Для этого, как и в предыдущем случае, выберем крайние точки M 1(x 1, y 1) и M n(x n, y n) и составим среднее арифметическое
Для 
найдём соответствующее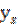 
(или из чертежа, или линейной интерполяцией). Представляя эти значения в эмпирическую формулу (4.23), будем иметь
; 
; 
.
Отсюда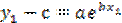 
; 
; 
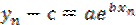. Следовательно
(
)(
) = 
; (
= 
;
(
)(
) =(
.
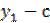Получим точно такое же уравнение, как и в предыдущем случае.
Поэтому с запишем в таком же виде
с = 
.
Если обнаружена линейная зависимость (4.24), то остальные параметры а и b находятся обычными приёмами.
Пример. Дана таблица 13
Таблица 13
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| у | 1,30 | 1,44 | 1,59 | 1,78 | 1,97 | 2,19 | 2,46 | 2,74 | 3,06 | 3,42 | 3,84 |
Найти эмпирическую формулу. Будем её искать в виде
y = aebx + c.
сначала найдём 
= 
= 0,5. Этому значению в данной таблице соответствует значение 
= 2,19. Отсюда
с =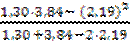 
= 0,258.
Параметры а и b определяем по методу средних. Для этого запишем
lg (y i – 0.258) = lg a + bMx i, (i = 1,2,…,10).
Составим две системы уравнений
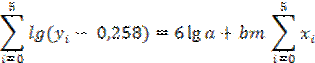
Подставив значения x i и y i и приведя подобные члены, получим систему двух уравнений
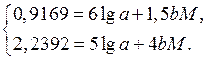
Решая эту систему найдём: а = 1,044; b = 1,234. Следовательно, эмпирическая формула имеет вид
у = 1,044е1,234 х +0,258.
Библиографический список
1. Бахвалов Н.С. и др. Численные методы. -М.: - СПб. Физматлит 2001. – 632с.
2. Кунцман Ж.Численные методы. -М.: Изд-во Наука, 1979.
3. Бахвалов Н.С. и др. Численные методы в задачах и примерах. – М.: Высшая школа, 2000.
4. Волков Е.А.Численные методы, – М.: Изд-во Наука, 1987.
5. Калиткин Н.Н. Численные методы.–М.: Изд-во Наука, 1978. –512с.
6. Демидович Б.П., Марон И.А. Основы вычислительной математики. -М.: Изд-во Наука, 1970. -664с.
7. Гуттер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта.–М.: Изд-во Наука, 1970. –432с.