Задача4. Доказать что, если радиус вневписанной окружности равен полупериметру треугольника, то треугольник будет прямоугольным. (Рис.12).
Дано:  . Доказать: треугольник прямоугольный
. Доказать: треугольник прямоугольный
| L |
| A |
| K |
| B |
| M |
| C |
| O |
| Рис.12 |
Доказательство:
Пусть вневписанная окружность (с центром О) треугольника АВС касается стороны АВ в точке К, а продолжений сторон СА и СВ – в точках L и M соответственно. Обозначим через р полупериметр треугольника.
Тогда P=АВ+ВС+АС=(АК+КВ)+ВС+АС=(АL+ВM)+ВС+АС=(АL+АС)+(ВM+ВС)=
= СL+СM.
Итак, СL+СМ=Р и ОL+ОМ= Р  четырёхугольник ОLСМ – ромб, а т.к. ОL СL, то это квадрат. Следовательно,<АСВ=900. Что и требовалось доказать.
четырёхугольник ОLСМ – ромб, а т.к. ОL СL, то это квадрат. Следовательно,<АСВ=900. Что и требовалось доказать.
Задача5. Обратная. Доказать, что полупериметр прямоугольного треугольника равен радиусу вневписанной окружности.(Рис.13).
Дано: треугольник прямоугольный. Доказать: 
Доказательство: пусть вневписанная окружность (с центром О) треугольника АВС касается стороны АВ в
точке К, а продолжений сторон СА и СВ – в точках L и M соответственно. Обозначим через р полупериметр треугольника. СМОL- квадрат, так как <C=900 по условию (∆АВС – прямоугольный), <L=<M=900 (OL┴CL).
| L |
| A |
| K |
| B |
| M |
| C |
| O |
| Рис.13 |
Тогда по свойству вневписанной окружности: CL+CM=Р
и OM ┴CM), ОL=ОM-радиус вневписанной окружности.
 ОL +CM=Р, СМ=ОL=r=
ОL +CM=Р, СМ=ОL=r=  Что и требовалось доказать.
Что и требовалось доказать.
Задача6. Высота равностороннего треугольника равна радиусу вневписанной окружности.(Рис.14).
Дано: ▲АВС равносторонний, сторона которого равна а, высота треугольника h. Радиус вневписанной окружности обозначим r. Докажем, что h=r.
Решение: 1.Т.к. ▲ АВС равносторонний, то высота АН является и медианой. СН=НВ= 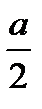 . Из треугольника АНВ по теореме Пифагора получим: h=АН=
. Из треугольника АНВ по теореме Пифагора получим: h=АН=  (1).
(1).
2. SABC=  - площадь равностороннего треугольника со стороной а.
- площадь равностороннего треугольника со стороной а.
| Рис. 14 |
| A |
| B |
| C |
| H |
| O |
| Mttp://www.problems.ru/view_by_subject_new.php?parent=600&start= |
| Tttp://www.problems.ru/view_by_subject_new.php?parent=600&start= |
3. По свойствам вневписанной окружности: r =  , здесь р- полупериметр треугольника АВС. Получим ra=
, здесь р- полупериметр треугольника АВС. Получим ra=  =
=  :(
:(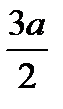 -а)=
-а)=  :
: 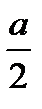 =
=  (2).
(2).
4. Из равенств (1) и (2)  h=r.
h=r.
Ответ: h=r.
Задача 7.
Дано: Точка О – центр вписанной окружности треугольника АВС, а точка О1 – центр окружности, касающейся стороны ВС и продолжений сторон АВ и АС.
| C |
| L |
| O |
| А |
| B |
| Рис15 |
Найдите расстояние между точками О и О1, если радиус описанной окружности треугольника АВС=6, а sin< ВОС =
 . (Рис. 15)
. (Рис. 15)
Решение:
1) Так как О – центр вписанной окружности ∆АВС, то АО, ВО, СО –биссектрисы углов этого треугольника. Прежде чем приступить к решению задачи, докажем следующее вспомогательное утверждение <ВОС=900+  <А.
<А.
В самом деле, <ВОС= <ВОL+<СОL, см. рис.7
<ВОL=<ВАО+<АВО=  <А+
<А+  <В (как внешний угол ∆АВО при вершине О), <СОL=<САО+<АСО=
<В (как внешний угол ∆АВО при вершине О), <СОL=<САО+<АСО=  <А+
<А+  <В (как внешний угол ∆АСО при вершине О)
<В (как внешний угол ∆АСО при вершине О)
Отсюда получаем: <ВОС=(  <А+
<А+  <В)+(
<В)+(  <А+
<А+  <В)=
<В)=  (<А+<В+<С)+
(<А+<В+<С)+  <А=900+
<А=900+  <А, что и требовалось доказать.
<А, что и требовалось доказать.
По условию, sin<BOC=  , следовательно sin(900+
, следовательно sin(900+  <А)=cos(
<А)=cos(  <А)=
<А)=  sin(
sin( <А)=
<А)=  .
.
2) (Рис.16)Так как точка О1 равноудалена от лучей АВ и АС, то она лежит на биссектрисе угла ВАС, а поскольку О1 равноудалена от стороны ВС и продолжения стороны АВ за точку В, то О1 лежит на биссектрисе внешнего угла ∆АВС при вершине В. Опишем вокруг треугольника АВС окружность, и пусть К – точка пересечения биссектрисы угла ВАС с этой окружностью, см. рис. 16
| М |
| О1 |
| К |
| C |
| L |
| O |
| А |
| B |
| Рис.16 |
Покажем, что <ОВО1=900: <СВО1=  <СВМ, <ОВО1=<СВО+<СВО1=
<СВМ, <ОВО1=<СВО+<СВО1=  <АВС+
<АВС+  <СВМ=
<СВМ=  ∙1800=900.
∙1800=900.
Следовательно, ОО1 является гипотенузой прямоугольного треугольника ОВО1. Заметим, что поскольку <СВК=<KАС (как вписанные углы, опирающиеся на одну дугу), то <ОВК=<СВК+<СВО=  <А+
<А+  <В. А поскольку <ВОК=
<В. А поскольку <ВОК=  <А+
<А+  <В (см. пункт 1 решения), то <ОВК=<ВОК, и, значит, ∆ВОК равнобедренный, ВК=ОК. Из равенства <ОВК=<ВОК следует, что <О1ВК=<ВО1К (<О1ВК=900-<ОВК, <ВО1К=900-<ВО1К). Поэтому ∆ВО1К также равнобедренный, ВК=О1К.
<В (см. пункт 1 решения), то <ОВК=<ВОК, и, значит, ∆ВОК равнобедренный, ВК=ОК. Из равенства <ОВК=<ВОК следует, что <О1ВК=<ВО1К (<О1ВК=900-<ОВК, <ВО1К=900-<ВО1К). Поэтому ∆ВО1К также равнобедренный, ВК=О1К.
3)Из равенств ВК=ОК и ВК=О1К получаем, что ОО1= 2ВК. Длину отрезка ВК найдём из треугольника АВК по теореме синусов: ВК=2R∙sin<ВAК. Так как sin<ВAК=sin(  <А)=
<А)=  (см. пункт 1 решения), а R=6 (по условию), то ВК= 2∙6∙
(см. пункт 1 решения), а R=6 (по условию), то ВК= 2∙6∙  =8, ОО1=2ВК=16.
=8, ОО1=2ВК=16.
Ответ:16
Задача 8.
Точка О – центр вписанной окружности треугольника АВС, а точка О1 – центр окружности, касающейся стороны ВС и продолжений сторон АВ и АС. Найдите длину ВС, если ОО1=12, а sin< ВО1С =  .
.
Решение:
| C |
| L |
| O |
| А |
| B |
| Рис.17 |
1.Так как О – центр вписанной окружности ∆АВС, то АО,
ВО, СО биссектрисы углов этого треугольника. Прежде чем приступить к решению задачи, докажем следующее вспомогательное утверждение <ВОС=900+  <А.
<А.
В самом деле, <ВОС= <ВОL+<СОL (рис17).
<ВОL=<ВАО+<АВО=  <А+
<А+  <В (как внешний угол ∆АВО при вершине О), <СОL=<САО+<АСО=
<В (как внешний угол ∆АВО при вершине О), <СОL=<САО+<АСО=  <А+
<А+  <В (как внешний угол ∆АСО при вершине О)
<В (как внешний угол ∆АСО при вершине О)
Отсюда получаем: <ВОС=(  <А+
<А+  <В)+(
<В)+(  <А+
<А+  <В)=
<В)=  (<А+<В+<С)+
(<А+<В+<С)+  <А=900+
<А=900+  <А, что и требовалось доказать.
<А, что и требовалось доказать.
 2). (Рис 18).Так как точка О1 равноудалена от лучей АВ и АС, то она лежит на биссектрисе угла ВАС, а поскольку О1 равноудалена от стороны ВС и продолжения стороны АВ за точку В, то О1 лежит на биссектрисе внешнего угла ∆АВС при вершине В. Опишем вокруг треугольника АВС окружность, и пусть К – точка пересечения биссектрисы угла ВАС с этой окружностью, см. рис.9
2). (Рис 18).Так как точка О1 равноудалена от лучей АВ и АС, то она лежит на биссектрисе угла ВАС, а поскольку О1 равноудалена от стороны ВС и продолжения стороны АВ за точку В, то О1 лежит на биссектрисе внешнего угла ∆АВС при вершине В. Опишем вокруг треугольника АВС окружность, и пусть К – точка пересечения биссектрисы угла ВАС с этой окружностью, см. рис.9
Покажем, что <ОВО1=900: <СВО1=  <СВМ, <ОВО1=<СВО+<СВО1=
<СВМ, <ОВО1=<СВО+<СВО1=  <АВС+
<АВС+  <СВМ=
<СВМ=  ∙1800=900.
∙1800=900.
Следовательно, ОО1 является гипотенузой прямоугольного треугольника ОВО1 . Заметим, что поскольку <СВК=<KАС (как вписанные углы, опирающиеся на одну дугу), то <ОВК=<СВК+<СВО=  <А+
<А+  <В. А поскольку <ВОК=
<В. А поскольку <ВОК=  <А+
<А+  <В (см. пункт 1 решения), то <ОВК=<ВОК, и, значит, ∆ВОК равнобедренный, ВК=ОК. Из равенства <ОВК=<ВОК следует, что < О1ВК=<ВО1К (<О1ВК=900-<ОВК, <ВО1К=900-<ВО1К). Поэтому ∆ВО1К также равнобедренный, ВК=О1К и <ВО1К=<КВО1.
<В (см. пункт 1 решения), то <ОВК=<ВОК, и, значит, ∆ВОК равнобедренный, ВК=ОК. Из равенства <ОВК=<ВОК следует, что < О1ВК=<ВО1К (<О1ВК=900-<ОВК, <ВО1К=900-<ВО1К). Поэтому ∆ВО1К также равнобедренный, ВК=О1К и <ВО1К=<КВО1.
2)Из равенств ВК=ОК и ВК=О1К и ОО1=12 получаем, что ВК=6, а также т.к. <ВО1К= <КО1С и <ВО1К=<КВО1, а <ВКL=<ВО1К+<КВО1 (как внешний угол ∆ КВО1 при вершине К).
| М |
| О1 |
| К |
| C |
| L |
| O |
| А |
| B |
| Рис.18 |
Следовательно sin<ВКL=  . Рассмотрим ∆ВКL – прямоугольный.
. Рассмотрим ∆ВКL – прямоугольный.  ,
,  , 3∙ВL=6, ВL=2. ВК=2R∙sin<ВAК. Так как sin<ВAК=
, 3∙ВL=6, ВL=2. ВК=2R∙sin<ВAК. Так как sin<ВAК=  , sin<ВAК=
, sin<ВAК=  , <ВAК=300, <ВAС=600, ∆АВС - равносторонний, АL- биссектриса, медиана. ВС=2∙ВL=2∙2=4.
, <ВAК=300, <ВAС=600, ∆АВС - равносторонний, АL- биссектриса, медиана. ВС=2∙ВL=2∙2=4.
Ответ: 4.
Литература
1.Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1996. – 648 с
2.Научно-практический журнал Математика для школьников №1 2011г.
3.https://www.problems.ru/view_by_subject_new.
4.Энциклопедия.Математика.-М:Мир энциклопедий Аванта+,2007,с.281.
5.Гнеденко Б.В. Энциклопедический словарь юного математика. - М.: «Педагогика», 1989.
6.Гохидзе М. Г. Вневписанная окружность. Математика в школе №3, 1989.
7. Д.А. Мальцев, А.А. Мальцев, Л.И. Мальцева. Математика. Всё для ЕГЭ 2011.─М.НИИшкольных технологий,2011.
8. Демонстрационный вариант ГИА,2013г.
9. Пробный экзамен ЕГЭ от 18.12.2012г.