МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Институт – Физико-технический
Направление (специальность) - Физика
Кафедра – Общей физики
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ:
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
| Выполнил: | магистрант гр. 0БМ71 | ____________ (Подпись) | ________ (Дата) | Е.А Кабдылкаков |
| Проверил: | доцент кафедры ТПТ (Должность) | _____________ (Подпись) | ________ (Дата) | Е.А. Маслов |
Томск – 2017
Содержание
1 Задание. 3
2 Метод решения СЛАУ.. 3
3 Проверка метода решения СЛАУ.. 9
Выводы.. 10
Список используемой литературы.. 10
Листинг программы метода решения СЛАУ.. 11
Задание
Методом прогонки решить систему линейных алгебраических уравнений (СЛАУ):
Метод решения СЛАУ
Метод прогонки используется для решения систем линейных уравнений вида Ax=D, где A – трёхдиагональная матрица. Представляет собой вариант метода последовательного исключения неизвестных. Метод прогонки был предложен И. М. Гельфандом и О. В. Локуциевским [1].
Метод прогонки является частным случаем метода Гаусса. Метод применяется для решения СЛАУ с трехдиагональными матрицами. Такие системы часто возникают при конечно-разностной аппроксимации задач для обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных второго порядка.
| 
|
| 
|
| 
|
| ................................................. | |
|
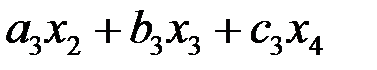
Отметим характерную особенность строк трехдиагональной матрицы (1):
 , 
| (2) |
при этом будем полагать, что
 
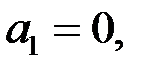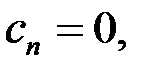
| (3) |
Таким образом, если построчно перебирая индексы от 1 до n используя выражение (2), с учетом (3), получим исходную систему (1).
Из первой строки системы (1) определяем 
:
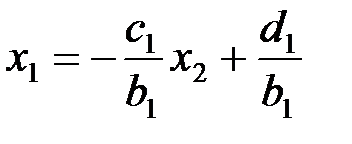
| (4) |
Перепишем полученное выражение, введя соответствующие обозначения:
| (5) |
Из второго уравнения системы (1) и с помощью (4) 
вырожаетсячерез 
, получим:
| (6) |
преобразуем полученное выражение, получим:
| (7) |
разрешим последнее выражение относительно , получим
| (8) |
Аналогично, полученное выше выражение можно привести к виду (5):
| (9) |
Где:
 
| (10) |
Из третьего уравнения системы (1) с помощью (5) выражая через 
, получим:
| (11) |
преобразуем полученное выражение, получим:
| (12) |
| (13) |
Аналогично, полученное выше выражение можно привести к виду (4)или (5):
| (14) |
Где:
 , 
| (15) |
Продолжая этот процесс, получим из i -го уравнения системы (1), с помощью (2) выразим 
через 
:
 ,
| (16) |
Преобразуем полученное выражение и разрешим относительно , получи:
| (17) |
Следовательно
 
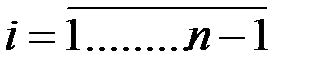
| (18) |
Где
, 
Из последнего уравнения системы (1) имеем:
| (19) |
Таккак 
 , 
| (20) |
Таким образом, прямой ход определения прогоночныхкоэфицентов 
и 
(i=1,2…n), завершен. В результате эти коэффициенты вычисляются по следующим формулам:
  
| (21) |
 ,  ,
| (22) |
 ,
| (23) |
Обратный ход метода прогонки осуществляется в соответствии с выражением (7). Операция осуществляется в обратном направлении (n …1).
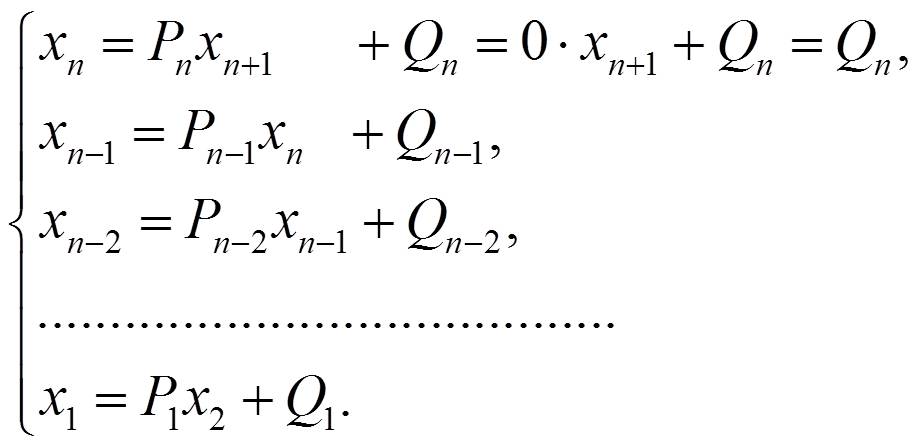
| (24) |
Формулы (21) – (24) являются формулами правой прогонки. Аналогично, начиная с последнего уравнения СЛАУ (1), можно вывести формулы левой прогонки.
Общее число операций в методе прогонки равно 8n+1, т.е. пропорционально числу уравнений. Такие методы решения СЛАУ называют экономичными. Для сравнения число операций в методе Гаусса пропорционально n3.
Для устойчивости метода прогонки (21) – (24) достаточно выполнение следующих условий:
Строгое неравенство имеет место хотя бы при одном i. Здесь устойчивость понимается в смысле накопления погрешности решения в ходе вычислительного процесса при малых погрешностях входных данных (правых частей и элементов матрицы СЛАУ).
Проверка метода решения СЛАУ
Для проверки метода прямой прогонки СЛАУ был взять решёный пример из учебного пособия [2].
Результаты проверки
Результат проверки прямой прогонки показал следующий результат:
+0.0x0+8.0x1+2.0x2=6.0
-1.0x1+6.0x2-2.0x3=3.0
+2.0x2+10.0x3-4.0x4=8.0
-1.0x3+6.0x4+0.0x5=5.0
P1=0.2500 Q1=0.7500
Pi=0.3478 Qi=0.6522
Pi=0.3740 Qi=0.6260
Pi=0.0000 Qi=1.0000
x1=1.0000
x2=1.0000
x3=1.0000
x4=1.0000
Выводы
Была решена система линейных алгебраических уравнений (СЛАУ) методом прогонки. В результае проверки программы значениеx получили значение целых чисел, а коэфиценты числе получили дробные значение.
Список используемой литературы
1. https://ru.wikipedia.org/wiki/Метод_прогонки
2. Численные методы. Сборник задач под. ред. У.Г.Пирумова
3. Гидаспов В.Ю., Иванов И.Э., Ревизников Д.Л. и др.Численные методы. Сборник задач: учеб. Пособие для вузов/В.Ю. Гидаспов, И.Э. Иванов, Д.Л. Ревизников и др.; под ред. У.Г. Пирумова. – М.: Дрофа, – 2007. – с. 144.
Листинг программы метода решения СЛАУ
Program Matrix;
const N=4;
type massiv= array [1..N] of real;
var i,j,k: integer;
z:real;
a,b,c,d,P,Q,x:Massiv;
Begin
a[1]:=0; b[1]:=8; c[1]:=2; d[1]:=6;
a[2]:=-1; b[2]:=6; c[2]:=-2; d[2]:=3;
a[3]:=2; b[3]:=10; c[3]:=-4; d[3]:=8;
a[4]:=-1; b[4]:=6; c[4]:=0; d[4]:=5;
for i:=1 to N do begin
if a[i]>=0 then write('+');
write(a[i]:3:1,'x',i-1);
if b[i]>=0 then write('+');
write (b[i]:3:1, 'x', i);
if c[i]>=0 then write('+');
write (c[i]:3:1, 'x', i+1);
write('=');
write (d[i]:3:1);
writeln;
end;
writeln;
P[1]:=c[1]/b[1];Q[1]:=d[1]/b[1];
writeln('P',1,'=',P[1]:5:4, ' Q',1, '=',Q[1]:5:4);
for i:=2 to N do begin
z:=a[i]* P[i-1]+b[i];
if abs(z)<0.00001 then begin
writeln ('error, division by zero');
readln;
halt;
end;
P[i]:=-c[i]/z;
Q[i]:=(d[i]- a[i]* Q[i-1])/Z;
writeln ('P' 'i', '=', P[i]:5:4,' Q' 'i', '=', Q[i]:5:4);
end;
writeln; x[N]:=Q[N];
for i:= N-1 downto 1 do
x[i]:= P[i]*x[i+1]+Q[i];
for i:=1 to N do
writeln('x', i, '=', x[i]:5:4);
End